Even at school, each of us studied equations and, for sure, systems of equations. But not many people know that there are several ways to solve them. Today we will analyze in detail all the methods for solving a system of linear algebraic equations, which consist of more than two equalities.
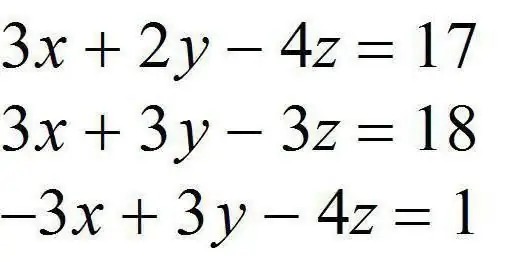
History
Today it is known that the art of solving equations and their systems originated in ancient Babylon and Egypt. However, equalities in their usual form appeared after the appearance of the equal sign "=", which was introduced in 1556 by the English mathematician Record. By the way, this sign was chosen for a reason: it means two parallel equal segments. Indeed, there is no better example of equality.
Founder of modern letter designations of unknowns and signs of degrees is the French mathematician Francois Viet. However, his designations differed significantly from today's. For example, he denoted the square of an unknown number with the letter Q (lat. "quadratus"), and the cube with the letter C (lat. "cubus"). These designations now seem inconvenient, but thenit was the most understandable way to write systems of linear algebraic equations.
However, the disadvantage of the then methods of solution was that mathematicians considered only positive roots. Perhaps this is due to the fact that negative values had no practical use. One way or another, it was the Italian mathematicians Niccolo Tartaglia, Gerolamo Cardano and Rafael Bombelli who were the first to consider negative roots in the 16th century. And the modern look, the main method for solving quadratic equations (through the discriminant) was created only in the 17th century thanks to the work of Descartes and Newton.
In the mid-18th century, the Swiss mathematician Gabriel Cramer found a new way to make solving systems of linear equations easier. This method was subsequently named after him and to this day we use it. But we will talk about the Cramer method a little later, but for now we will discuss linear equations and methods for solving them separately from the system.

Linear equations
Linear equations are the simplest equalities with variable(s). They are classified as algebraic. Linear equations are written in general form as follows: 2+…a x =b. We will need their representation in this form when compiling systems and matrices further.
Systems of linear algebraic equations
The definition of this term is this: it is a set of equations that have common unknowns and a common solution. As a rule, at school everything was decided by systemswith two or even three equations. But there are systems with four or more components. Let's first figure out how to write them down so that it is convenient to solve them later. First, systems of linear algebraic equations will look better if all variables are written as x with the appropriate index: 1, 2, 3, and so on. Secondly, all equations should be reduced to the canonical form: a1x1+a2 x2+…a x =b.
After all these steps, we can start talking about how to find a solution to systems of linear equations. Matrices will be very useful for this.
Matrices
A matrix is a table that consists of rows and columns, and its elements are located at their intersection. These can either be specific values or variables. Most often, to designate elements, subscripts are placed under them (for example, a11 or a23). The first index means the row number and the second one the column number. On matrices, as well as on any other mathematical element, you can perform various operations. So you can:
1) Subtract and add tables of the same size.
2) Multiply a matrix by some number or vector.
3) Transpose: Turn matrix rows into columns and columns into rows.
4) Multiply matrices if the number of rows of one of them is equal to the number of columns of the other.
We will discuss all these techniques in more detail, as they will be useful to us in the future. Subtracting and adding matrices is very easy. Soas we take matrices of the same size, then each element of one table corresponds to each element of another. Thus, we add (subtract) these two elements (it is important that they are in the same places in their matrices). When multiplying a matrix by a number or vector, you simply need to multiply each element of the matrix by that number (or vector). Transposition is a very interesting process. It is very interesting sometimes to see it in real life, for example, when changing the orientation of a tablet or phone. The icons on the desktop are a matrix, and when you change the position, it transposes and becomes wider, but decreases in height.
Let's take another look at such a process as matrix multiplication. Although it will not be useful to us, it will still be useful to know it. You can multiply two matrices only if the number of columns in one table is equal to the number of rows in the other. Now let's take the elements of a row of one matrix and the elements of the corresponding column of another. We multiply them by each other and then add them (that is, for example, the product of the elements a11 and a12 by b12and b22 will be equal to: a11b12 + a12 b22). Thus, one element of the table is obtained, and it is filled further by a similar method.
Now we can start looking at how the system of linear equations is solved.

Gauss method
This topic begins to pass even at school. We know well the concept of "system of two linear equations" and know how to solve them. But what if the number of equations is more than two? The Gauss method will help us with this.
Of course, this method is convenient to use if you make a matrix out of the system. But you can not transform it and solve it in its purest form.
So how does this method solve the system of linear Gaussian equations? By the way, although this method is named after him, it was discovered in ancient times. Gauss proposes the following: to carry out operations with equations in order to eventually reduce the entire set to a stepped form. That is, it is necessary that from top to bottom (if placed correctly) from the first equation to the last, one unknown decreases. In other words, we need to make sure that we get, say, three equations: in the first - three unknowns, in the second - two, in the third - one. Then from the last equation we find the first unknown, substitute its value into the second or first equation, and then find the remaining two variables.

Cramer method
To master this method, it is vital to master the skills of addition, subtraction of matrices, and you also need to be able to find determinants. Therefore, if you do all this poorly or do not know how at all, you will have to learn and practice.
What is the essence of this method, and how to make it so that a system of linear Cramer equations is obtained? Everything is very simple. We have to construct a matrix from numerical (almost always) coefficients of a system of linear algebraic equations. To do this, simply take the numbers in front of the unknowns and arrange them intable in the order in which they are recorded in the system. If the number is preceded by a "-" sign, then we write down a negative coefficient. So, we have compiled the first matrix from the coefficients of the unknowns, not including the numbers after the equal signs (naturally, the equation should be reduced to the canonical form, when only the number is on the right, and all the unknowns with coefficients on the left). Then you need to create several more matrices - one for each variable. To do this, we replace in turn each column with coefficients in the first matrix with a column of numbers after the equal sign. Thus, we obtain several matrices and then find their determinants.
After we have found the determinants, the matter is small. We have an initial matrix, and there are several resulting matrices that correspond to different variables. To get the solutions of the system, we divide the determinant of the resulting table by the determinant of the initial table. The resulting number is the value of one of the variables. Similarly, we find all unknowns.

Other methods
There are several more methods to get the solution of systems of linear equations. For example, the so-called Gauss-Jordan method, which is used to find solutions to a system of quadratic equations and is also associated with the use of matrices. There is also a Jacobi method for solving a system of linear algebraic equations. It is the easiest to adapt to a computer and is used in computing.
Difficult cases
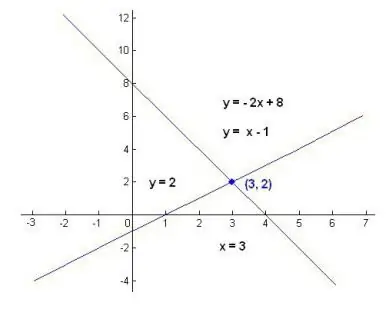
Complexity usually occurs when the number of equations is less than the number of variables. Then we can say for sure that either the system is inconsistent (that is, it has no roots), or the number of its solutions tends to infinity. If we have the second case, then we need to write down the general solution of the system of linear equations. It will contain at least one variable.
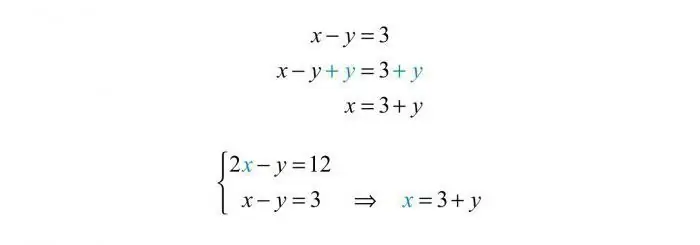
Conclusion
Here we come to the end. Let's summarize: we have analyzed what a system and a matrix are, learned how to find a general solution to a system of linear equations. In addition, other options were considered. We found out how the system of linear equations is solved: the Gauss method and the Cramer method. We talked about difficult cases and other ways to find solutions.
In fact, this topic is much more extensive, and if you want to better understand it, we advise you to read more specialized literature.






