Planimetry is an important branch of geometry that studies plane figures. The main property of all such elements is the area they occupy. Consider in the article what formulas are used to calculate the area of a circle.
What is this?
Obviously, before calculating the area of a circle, one should give a geometric definition of the figure. It is understood as a set of points on a plane that are located from a specific point O at a distance less than or equal to R. The point O is called the center of the circle, and R is its radius.
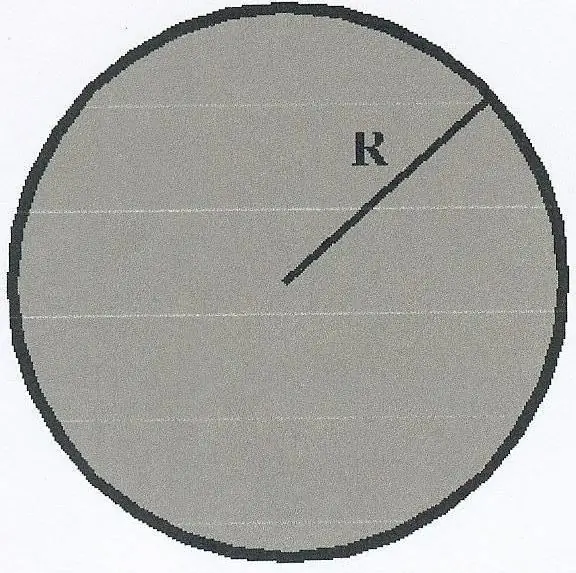
Unlike a circle, a circle has a certain area. The circle encloses the circle. Its length is the perimeter of the figure being studied.
In addition to the radius and center, a circle is also characterized by a diameter D. It is any segment that passes through the center of the figure.
A circle can be obtained by taking a segment, fixing one of its ends on a plane, and rotating the free end around the fixed point by 360 o. In this case, the length of the segment will be the radius of the figure.
Formulas for calculating the area of a circle
The area of a figure is called the area of the plane, which is bounded by a circle. Let us immediately find out that the area of the figure under consideration cannot be determined exactly, however, this accuracy can be increased to any significant figure after the decimal point. The thing is that the area formula contains the number Pi (pi). Its approximate value was already known in ancient Egypt. However, with an accuracy of several digits after the decimal point, it was determined by Leonhard Euler in 1737. He also proposed to call it "the number of Pi". It is 3, 14159 to five digits of precision.
The area of a circle is calculated using the following formulas:
S=pir2;
S=pid2 / 4;
S=Lr / 2.
The first two equalities are clear because they use an expression for the relationship between radius and diameter. As for the third formula, it is obtained by using the expression for the perimeter of the circle L. Recall that L=2pir.
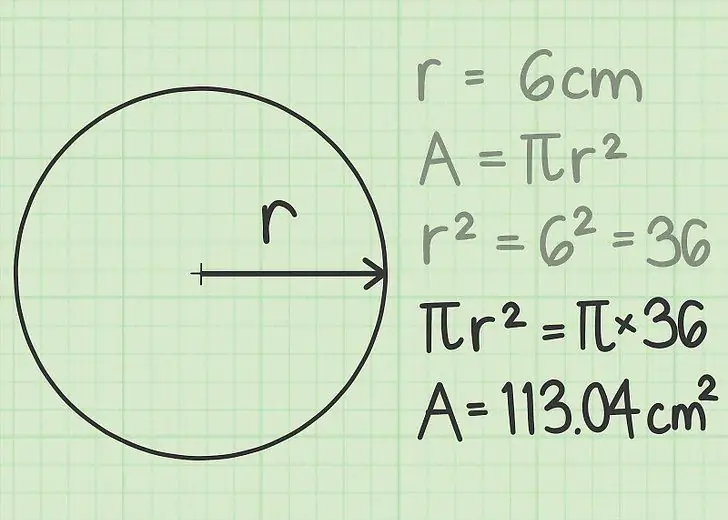
In the picture above you can see an example of solving the problem. The area in this case is indicated by the letter A.






