Inscribed quadrilateral in a circle. Quadrilateral ABCD is inscribed in a circle

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

With the division of mathematics into algebra and geometry, the educational material becomes more difficult. New figures and their special cases appear. In order to understand the material well, it is necessary to study the concepts, properties of objects and related theorems.

General concepts

A quadrilateral means a geometric figure. It consists of 4 points. Moreover, 3 of them are not located on the same straight line. There are segments connecting the specified points in series.

All quadrilaterals studied in the school geometry course are shown in the following diagram. Conclusion: any object from the presented figure has the properties of the previous figure.

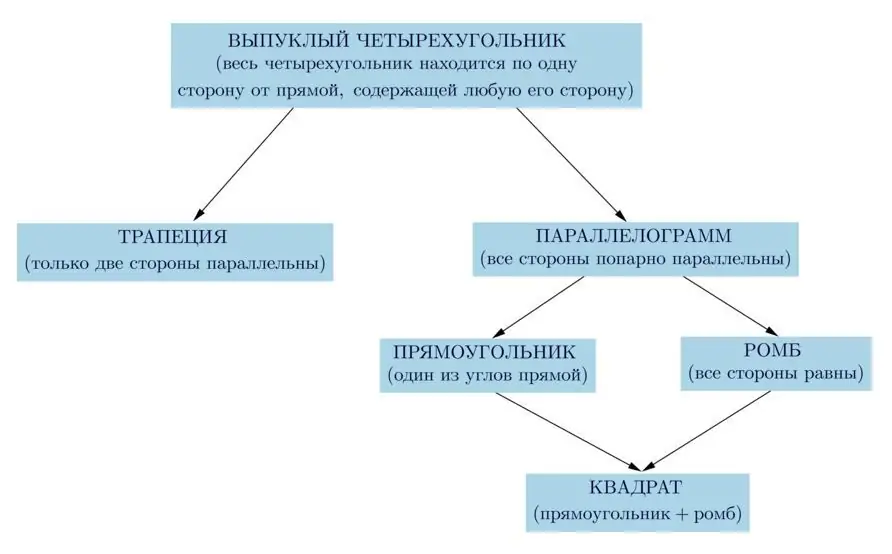
A quadrilateral can be of the following types:

• Parallelogram. The parallelism of its opposite sides is proved by the corresponding theorems.
• Trapeze. A quadrilateral with parallel bases. The other two parties are not.
• Rectangle. A figure that has all 4 corners=90º.
• Rhombus. A figure with all sides equal.
• Square. Combines the properties of the last two figures. It has all sides equal and all angles are right.

The main definition of this topic is a quadrilateral inscribed in a circle. It consists in the following. This is a figure around which a circle is described. It must pass through all vertices. The interior angles of a quadrilateral inscribed in a circle add up to 360º.

Not every quadrilateral can be inscribed. This is due to the fact that the perpendicular bisectors of the 4 sides may not intersect at one point. This will make it impossible to find the center of a circle circumscribing a 4-gon.

Special cases

There are exceptions to every rule. So, in this topic there are also special cases:

• A parallelogram, as such, cannot be inscribed in a circle. Only his special case. It's a rectangle.
• If all vertices of a rhombus are on the circumscribing line, then it is a square.
• All vertices of the trapezoid are on the boundary of the circle. In this case, they speak of an isosceles figure.

Properties of an inscribed quadrilateral in a circle

Before solving simple and complex problems on a given topic, you need to verify your knowledge. Without studying the educational material, it is impossible to solve a single example.

Theorem 1

The sum of the opposite angles of a quadrangle inscribed in a circle is 180º.

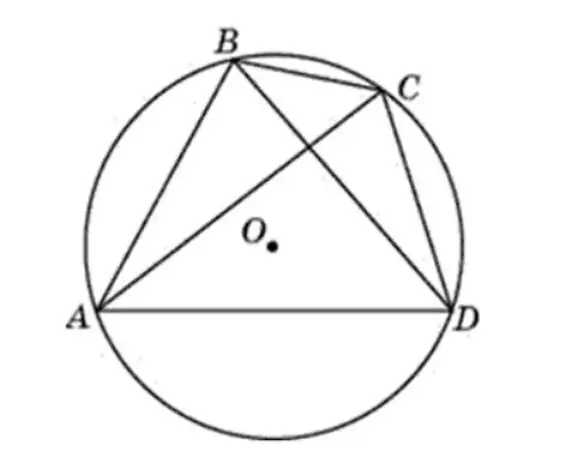
Proof

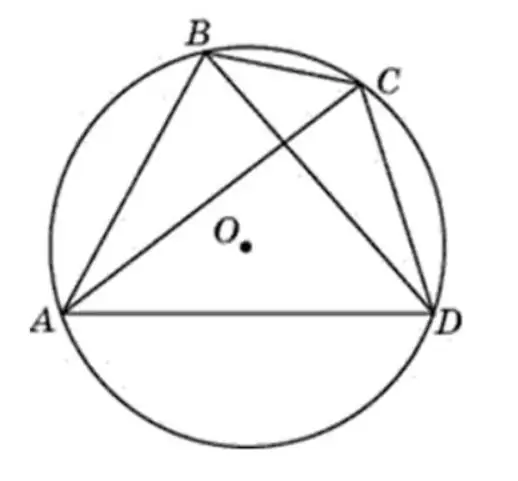
Given: quadrilateral ABCD is inscribed in a circle. Its center is point O. We need to prove that _<A + _<C=180º and _<B + _<D=180º.

Need to consider the presented figures.

1. _{<A is inscribed in a circle centered at point O. It is measured through ½ BCD (half arc).}
2. _{<C is inscribed in the same circle. It is measured through ½ BAD (half-arc).}
3. BAD and BCD form a whole circle, i.e. their magnitude is 360º.
4. _<A + _{<C are equal to half the sum of the half-arcs represented.}
5. Hence _<A + _{<C=360º / 2=180º.}

In a similar way, the proof for _<B and _{<D. However, there is a second solution to the problem.}

1. It is known that the sum of the interior angles of a quadrilateral is 360º.
2. Because _<A + _<C=180º. Accordingly, _<B + _{<D=360º – 180º=180º.}

Theorem 2

(It is often called inverse) If in a quadrilateral _<A + _<C=180º and _{< B +} <_{D=180º (if they are opposite), then a circle can be described around such a figure.}

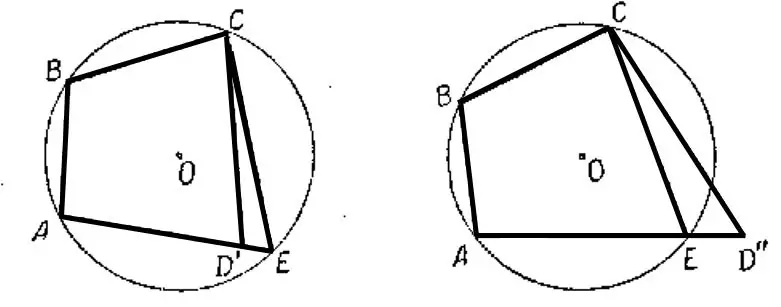
Proof

The sum of opposite angles of quadrilateral ABCD equal to 180º is given. _<A + _<C=180º, _<B +_{<D=180º. We need to prove that a circle can be circumscribed around ABCD.}

From the geometry course it is known that a circle can be drawn through 3 points of a quadrilateral. For example, you can use points A, B, C. Where will point D be located? There are 3 guesses:

1. She ends up inside the circle. In this case, D does not touch the line.
2. Outside the circle. She steps far beyond the outlined line.
3. It turns out on a circle.

It should be assumed that D is inside the circle. The place of the indicated vertex is occupied by D´. It turns out quadrilateral ABCD´.

The result is:_<B + _<D´=2d.

If we continue AD´ to the intersection with the existing circle centered at point E and connect E and C, we get an inscribed quadrilateral ABCE. From the first theorem follows the equality:

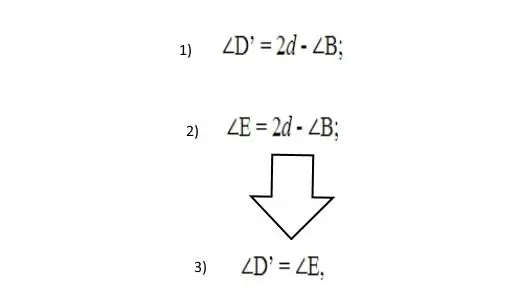
According to the laws of geometry, the expression is not valid because _<D´ is the outer corner of triangle CD´E. Accordingly, it should be more than _{<E. From this we can conclude that D must be either on the circle or outside it.}

Similarly, the third assumption can be proven wrong when D´´ goes beyond the boundary of the described figure.

From two hypotheses follows the only correct one. Vertex D is located on the circle line. In other words, D coincides with E. It follows that all points of the quadrilateral are located on the described line.

From thesetwo theorems, the corollaries follow:

Any rectangle can be inscribed in a circle. There is another consequence. A circle can be circumscribed around any rectangle

Trapezoid with equal hips can be inscribed in a circle. In other words, it sounds like this: a circle can be described around a trapezoid with equal edges

Several examples

Problem 1. Quadrilateral ABCD is inscribed in a circle. _<ABC=105º, _<CAD=35º. Need to find _{<ABD. Answer must be written in degrees.}

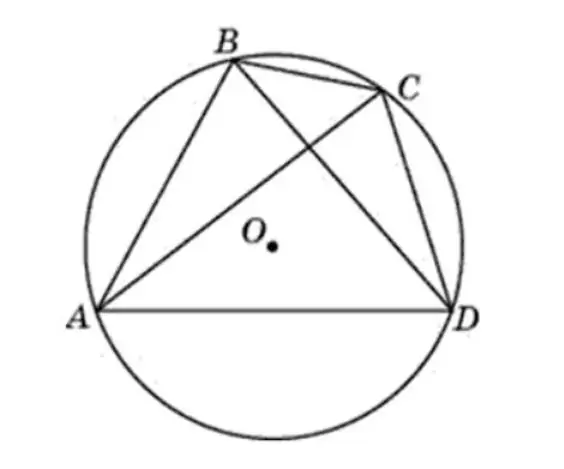
Decision. At first, it may seem difficult to find the answer.

1. You need to remember the properties from this topic. Namely: the sum of opposite angles=180º.

_<ADC=180º – _{<ABC=180º – 105º=75º}

In geometry, it's better to stick to the principle: find everything you can. Useful later.

2. Next step: use the triangle sum theorem.

_<ACD=180º – _<CAD – _{<ADC=180º – 35º – 75º=70º}

_<ABD and _{<ACD are inscribed. By condition, they rely on one arc. Accordingly, they have equal values:}

_<ABD=_<ACD=70º

Answer: _<ABD=70º.

Problem 2. BCDE is an inscribed quadrilateral in a circle. _<B=69º, _<C=84º. The center of the circle is point E. Find - _<E.

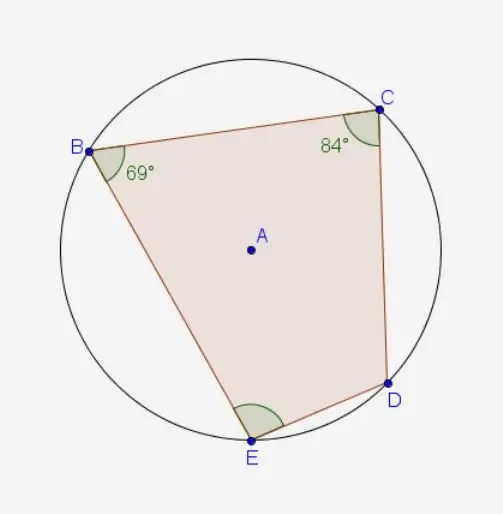
Decision.

1. Need to find _{<E by Theorem 1.}

_<E=180º – _{<C=180º – 84º=96º}

Answer: _{< E=96º.}

Problem 3. Given a quadrilateral inscribed in a circle. The data is shown in the figure. It is necessary to find unknown values x, y, z.

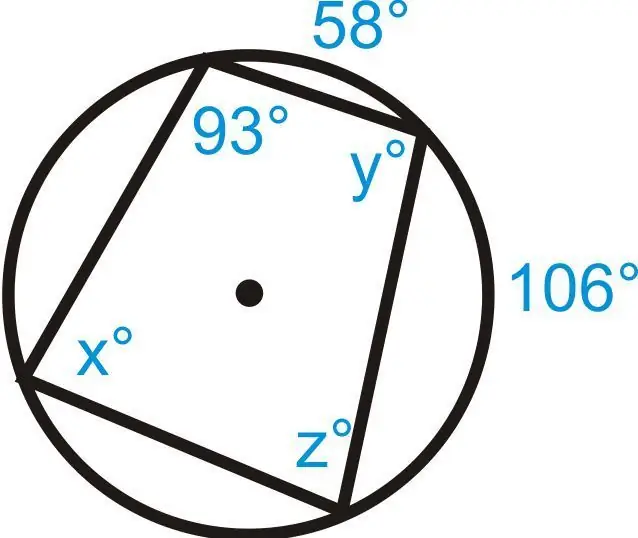
Solution:

z=180º – 93º=87º (by Theorem 1)

x=½(58º + 106º)=82º

y=180º – 82º=98º (by Theorem 1)

Answer: z=87º, x=82º, y=98º.

Problem 4. There is a quadrilateral inscribed in a circle. The values are shown in the figure. Find x, y.

Solution:

x=180º – 80º=100º

y=180º – 71º=109º

Answer: x=100º, y=109º.

Problems for independent solution

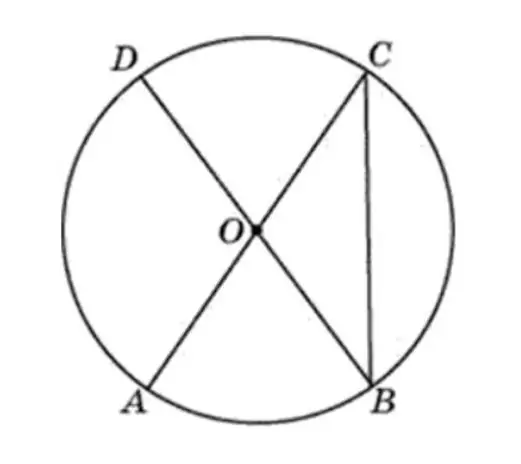
Example 1. Given a circle. Its center is point O. AC and BD are diameters. _<ACB=38º. Need to find _{<AOD. Answer must be given in degrees.}

Example 2. Given a quadrilateral ABCD and a circle circumscribed around it. _<ABC=110º, _<ABD=70º. Find _{<CAD. Write your answer in degrees.}

Example 3. Given a circle and an inscribed quadrilateral ABCD. Its two angles are 82º and58º. You need to find the largest of the remaining angles and write down the answer in degrees.

Example 4. Quadrilateral ABCD is given. Angles A, B, C are given in the ratio 1:2:3. It is necessary to find the angle D if the specified quadrilateral can be inscribed in a circle. Answer must be given in degrees.

Example 5. Quadrilateral ABCD is given. Its sides form arcs of the circumscribed circle. Degree values AB, BC, CD and AD, respectively, are: 78˚, 107˚, 39˚, 136˚. You should find _{<From the given quadrangle and write down the answer in degrees.}