The propagation of electromagnetic waves in various media obeys the laws of reflection and refraction. From these laws, under certain conditions, one interesting effect follows, which in physics is called the total internal reflection of light. Let's take a closer look at what this effect is.
Reflection and refraction
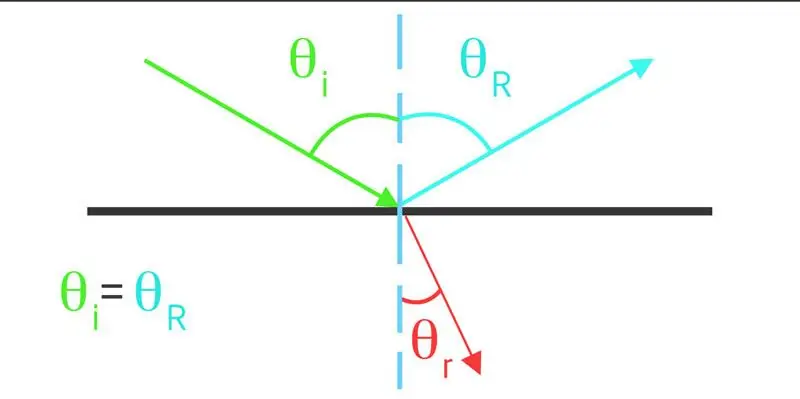
Before proceeding directly to the consideration of the internal total reflection of light, it is necessary to give an explanation of the processes of reflection and refraction.
Reflection is understood as a change in the direction of a light beam in the same medium when it encounters an interface. For example, if you direct a light beam from a laser pointer at a mirror, you can observe the described effect.
Refraction is, like reflection, a change in the direction of light movement, but not in the first, but in the second medium. The result of this phenomenon will be a distortion of the outlines of objects and theirspatial location. A common example of refraction is the breaking of a pencil or pen if he/she is placed in a glass of water.
Refraction and reflection are related to each other. They are almost always present together: part of the energy of the beam is reflected, and the other part is refracted.
Both phenomena are the result of Fermat's principle. He claims that light travels along the path between two points that takes him the least time.
Since reflection is an effect that occurs in one medium, and refraction occurs in two media, it is important for the latter that both media are transparent to electromagnetic waves.
The concept of refractive index

The refractive index is an important quantity for the mathematical description of the phenomena under consideration. The refractive index of a particular medium is defined as follows:
n=c/v.
Where c and v are the speeds of light in vacuum and matter, respectively. The value of v is always less than c, so the exponent n will be greater than one. The dimensionless coefficient n shows how much light in a substance (medium) will lag behind light in a vacuum. The difference between these speeds leads to the occurrence of the phenomenon of refraction.
The speed of light in matter correlates with the density of the latter. The denser the medium, the harder it is for light to move in it. For example, for air n=1.00029, that is, almost like for vacuum, for water n=1.333.
Reflections, refraction and their laws

The basic laws of light refraction and reflection can be written as follows:
- If you restore the normal to the point of incidence of a beam of light on the boundary between two media, then this normal, together with the incident, reflected and refracted rays, will lie in the same plane.
- If we designate the angles of incidence, reflection and refraction as θ1, θ2, and θ3, and the refractive indices of the 1st and 2nd medium as n1 and n2, then the following two formulas will be valid:
- to reflect θ1=θ2;
- for refraction sin(θ1)n1 =sin(θ3)n2.
Analysis of the formula for the 2nd law of refraction
To understand when the internal total reflection of light will occur, one should consider the law of refraction, which is also called Snell's law (a Dutch scientist who discovered it at the beginning of the 17th century). Let's write the formula again:
sin(θ1)n1 =sin(θ3) n2.
It can be seen that the product of the sine of the beam angle to the normal and the refractive index of the medium in which this beam propagates is a constant value. This means that if n1>n2, then in order to fulfill the equality it is necessary that sin(θ1)<sin(θ3). That is, when moving from a denser medium to a less dense one (meaning the opticaldensity), the beam deviates from the normal (the sine function increases for angles from 0o to 90o). Such a transition occurs, for example, when a beam of light crosses the water-air boundary.
The phenomenon of refraction is reversible, that is, when moving from a less dense to a denser one (n1<n2) the beam will approach the normal (sin(θ1)>sin(θ3)).
Internal total light reflection

Now let's get to the fun part. Consider the situation when the light beam passes from a denser medium, that is, n1>n2. In this case, θ1<θ3. Now we will gradually increase the angle of incidence θ1. The angle of refraction θ3 will also increase, but since it is larger than θ1, it will become equal to 90o earlier . What does θ3=90o mean from a physical point of view? This means that all the energy of the beam, when it hits the interface, will propagate along it. In other words, the refracting beam will not exist.
Further increase in θ1 will cause the entire beam to be reflected from the surface back to the first medium. This is the phenomenon of internal total reflection of light (refraction is completely absent).
The angle θ1, at which θ3=90o, is called critical for this pair of media. It is calculated according to the following formula:
θc =arcsin(n2/n1).
This equality follows directly from the 2nd law of refraction.
If the velocities v1and v2of propagation of electromagnetic radiation in both transparent media are known, then the critical angle is calculated by the following formula:
θc =arcsin(v1/v2).
It should be understood that the main condition for internal total reflection is that it exists only in an optically denser medium surrounded by a less dense one. So, at certain angles, the light coming from the seabed can be completely reflected from the surface of the water, but at any angle of incidence from the air, the beam will always penetrate into the water column.
Where is the effect of total reflection observed and applied?
The most famous example of the use of the phenomenon of internal total reflection is fiber optics. The idea is that due to the 100% reflection of light from the surface of the media, it is possible to transmit electromagnetic energy over arbitrarily long distances without loss. The working material of the fiber optic cable, from which its inner part is made, has a higher optical density than the peripheral material. Such a composition is sufficient to successfully use the effect of total reflection for a wide range of angles of incidence.
Glittering diamond surfaces are a prime example of the result of total reflection. The refractive index for a diamond is 2.43, so many rays of light hitting a gem experiencemultiple full reflection before exiting.

The problem of determining the critical angle θc for diamond
Let's consider a simple problem, where we will show how to use the given formulas. It is necessary to calculate how much the critical angle of total reflection will change if a diamond is placed from air into water.
Having looked at the values for the refractive indices of the indicated media in the table, we write them out:
- for air: n1=1, 00029;
- for water: n2=1, 333;
- for diamond: n3=2, 43.
The critical angle for a diamond-air pair is:
θc1=arcsin(n1/n3)=arcsin(1, 00029/2, 43) ≈ 24, 31o.
As you can see, the critical angle for this pair of media is quite small, that is, only those rays can leave the diamond into the air that will be closer to the normal than 24, 31o.
For the case of a diamond in water, we get:
θc2=arcsin(n2/n3)=arcsin(1, 333/2, 43) ≈ 33, 27o.
The increase in the critical angle was:
Δθc=θc2- θc1≈ 33, 27 o - 24, 31o=8, 96o.
This slight increase in the critical angle for the total reflection of light in a diamond causes it to shine in water almost the same as in air.






