Typical lighting effects that every person often encounters in everyday life are reflection and refraction. In this article, we will consider the case when both effects manifest themselves within the same process, we will talk about the phenomenon of internal total reflection.
Light reflection
Before considering the phenomenon of internal total reflection of light, you should get acquainted with the effects of ordinary reflection and refraction. Let's start with the first one. For simplicity, we will consider only light, although these phenomena are characteristic of a wave of any nature.
Reflection is understood as a change of one rectilinear trajectory, along which a ray of light moves, to another rectilinear trajectory, when it encounters an obstacle on its way. This effect can be observed when pointing a laser pointer at a mirror. The appearance of images of the sky and trees when looking at the water surface is also the result of the reflection of sunlight.

The following law is valid for reflection: anglesincidence and reflection lie in the same plane along with the perpendicular to the reflecting surface and are equal to each other.
Refraction of light
The effect of refraction is similar to reflection, only it occurs if the obstacle in the path of the light beam is another transparent medium. In this case, part of the initial beam is reflected from the surface, and part passes into the second medium. This last part is called the refracted beam, and the angle it makes with the perpendicular to the interface is called the angle of refraction. The refracted beam lies in the same plane as the reflected and incident beam.
Strong examples of refraction are the break of a pencil in a glass of water or the deceptive depth of a lake when a person looks down on its bottom.

Mathematically, this phenomenon is described using Snell's law. The corresponding formula looks like this:
1 sin (θ1)=n2 sin (θ 2).
Here the angles of incidence and refraction are denoted as θ1 and θ2 respectively. The quantities n1, n2 reflect the speed of light in each medium. They are called the refractive indices of the media. The larger n, the slower the light travels in a given material. For example, in water the speed of light is 25% less than in air, so for it the refractive index is 1.33 (for air it is 1).
The phenomenon of total internal reflection
The law of refraction of light leads to onean interesting result when the ray propagates from a medium with large n. Let us consider in more detail what will happen to the beam in this case. Let's write out Snell's formula:
1 sin (θ1)=n2 sin (θ 2).
We will assume that n1>n2. In this case, for the equality to remain true, θ1 must be less than θ2. This conclusion is always valid, since only angles from 0o to 90o are considered, within which the sine function is constantly increasing. Thus, when leaving a denser optical medium for a less dense one (n1>n2), the beam deviates more from the normal.
Now let's increase the angle θ1. As a result, the moment will come when θ2 will be equal to 90o. An amazing phenomenon occurs: a beam emitted from a denser medium will remain in it, that is, for it the interface between two transparent materials will become opaque.
Critical angle
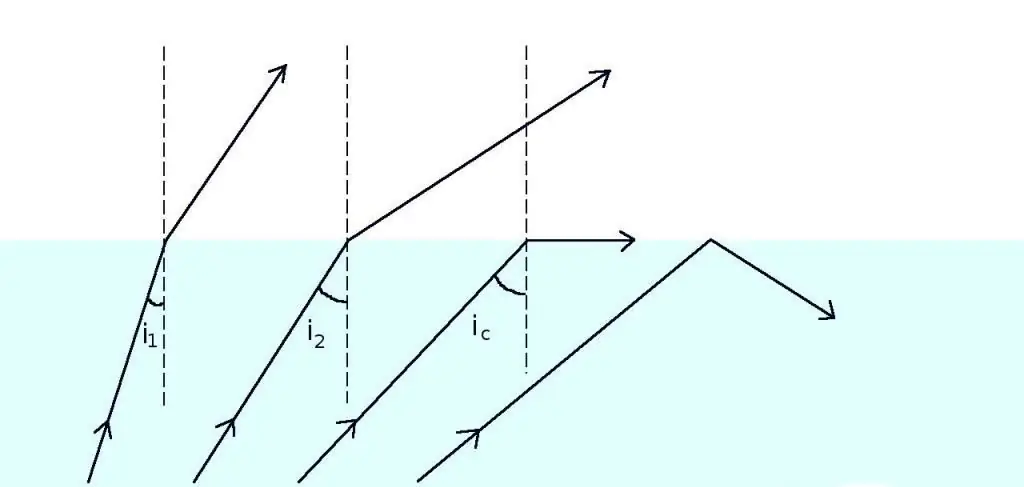
The angle θ1, for which θ2=90o, is called critical for the considered pair of media. Any ray that strikes the interface at an angle greater than the critical angle is reflected completely into the first medium. For the critical angle θc one can write an expression that directly follows from Snell's formula:
sin (θc)=n2 / n1.
Ifthe second medium is air, then this equality is simplified to the form:
sin (θc)=1 / n1.
For example, the critical angle for water is:
θc=arcsin (1 / 1, 33)=48, 75o.
If you dive to the bottom of the pool and look up, you can see the sky and clouds running across it only above your own head, on the rest of the water surface only the walls of the pool will be visible.
From the above reasoning, it is clear that, unlike refraction, total reflection is not a reversible phenomenon, it occurs only when moving from a denser to a less dense medium, but not vice versa.
Total reflection in nature and technology
Perhaps the most common effect in nature, which is impossible without total reflection, is the rainbow. The colors of the rainbow are the result of the dispersion of white light in raindrops. However, when the rays pass inside these droplets, they experience either single or double internal reflection. That is why the rainbow always appears double.
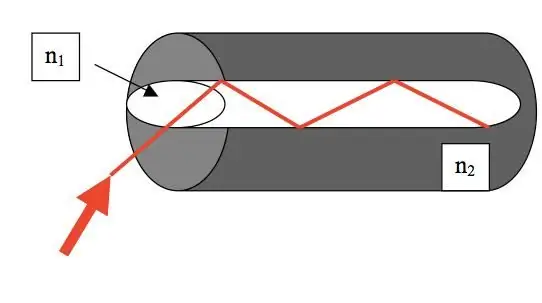
The phenomenon of internal total reflection is used in fiber optic technology. Thanks to optical fibers, electromagnetic waves can be transmitted without loss over long distances.






