Polynomial, or polynomial - one of the basic algebraic structures, which is found in school and higher mathematics. The study of a polynomial is the most important topic in an algebra course, since, on the one hand, polynomials are quite simple compared to other types of functions, and, on the other hand, they are widely used in solving problems of mathematical analysis. So what is a polynomial?
Definition
The definition of the term polynomial can be given through the concept of a monomial, or monomial.
A monomial is an expression of the form cx1i1x2i2 …x in. Here с is a constant, x1, x2, … x - variables, i1, i2, … in - exponents of variables. Then a polynomial is any finite sum of monomials.
To understand what a polynomial is, you can look at specific examples.
The square trinomial, discussed in detail in the 8th grade math course, is a polynomial: ax2+bx+c.
A polynomial with two variables might look like this: x2-xy+y2. Sucha polynomial is also called an incomplete square of the difference between x and y.
Polynomial classifications
Polynomial degree
For each monomial in the polynomial, find the sum of the exponents i1+i2+…+in. The largest of the sums is called the exponent of the polynomial, and the monomial corresponding to this sum is called the highest term.
By the way, any constant can be considered a polynomial of degree zero.
Reduced and non-reduced polynomials
If the coefficient c is equal to 1 for the highest term, then the polynomial is given, otherwise it is not.
For example, the expression x2+2x+1 is a reduced polynomial, and 2x2+2x+1 is not reduced.
Homogeneous and inhomogeneous polynomials
If the degrees of all members of a polynomial are equal, then we say that such a polynomial is homogeneous. All other polynomials are considered non-homogeneous.
Homogeneous polynomials: x2-xy+y2, xyz+x3 +y3. Heterogeneous: x+1, x2+y.
There are special names for a polynomial of two and three terms: binomial and trinomial, respectively.
Polynomials of one variable are allocated into a separate category.
Application of a polynomial of one variable
Polynomials of one variable approximate well continuous functions of varying complexity from one argument.
The fact is that such polynomials can be considered as partial sums of a power series, and a continuous function can be represented as a series with an arbitrarily small error. The expansion series of a function are called Taylor series, and theirpartial sums in the form of polynomials - Taylor polynomials.
Studying graphically the behavior of a function by approximating it with some polynomial is often easier than investigating the same function directly or using a series.
It is easy to look for derivatives of polynomials. To find the roots of polynomials of degree 4 and below, there are ready-made formulas, and for working with higher degrees, high-precision approximate algorithms are used.
There is also a generalization of the described polynomials for functions of several variables.
Newton's binomial
Famous polynomials are Newton's polynomials, derived by scientists to find the coefficients of the expression (x + y).
It is enough to look at the first few powers of the binomial decomposition to make sure that the formula is non-trivial:
(x+y)2=x2+2xy+y2;
(x+y)3=x3+3x2y+3xy 2+y3;
(x+y)4=x4+4x3y+6x 2y2+4xy3+y4;
(x+y)5=x5+5x4y+10x 3y2+10x2y3+5xy 4+y5.
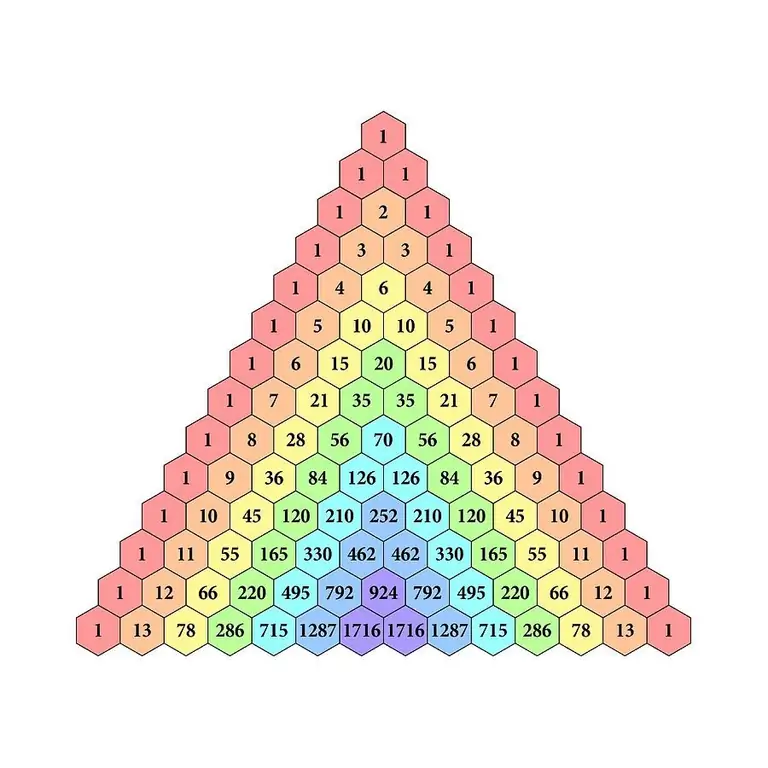
For each coefficient there is an expression that allows you to calculate it. However, memorizing cumbersome formulas and performing the necessary arithmetic operations each time would be extremely inconvenient for those mathematicians who often need such expansions. Pascal's triangle made life much easier for them.
The figure is built according to the following principle. 1 is written at the top of the triangle, and in each next line it becomes one more digit, 1 is put at the edges, and the middle of the line is filled with the sums of two adjacent numbers from the previous one.
When you look at the illustration, everything becomes clear.
Of course, the use of polynomials in mathematics is not limited to the given examples, the most widely known ones.






