The ability to determine the volume of spatial figures is important for solving geometric and practical problems. One of these figures is a prism. We will consider in the article what it is and show how to calculate the volume of an inclined prism.
What is meant by a prism in geometry?
This is a regular polyhedron (polyhedron), which is formed by two identical bases located in parallel planes, and several parallelograms connecting the marked bases.
Prism bases can be arbitrary polygons, such as triangle, quadrilateral, heptagon, and so on. Moreover, the number of corners (sides) of the polygon determines the name of the figure.
Any prism with an n-gon base (n is the number of sides) consists of n+2 faces, 2 × n vertices and 3 × n edges. From the given numbers it can be seen that the number of elements of the prism correspond to Euler's theorem:
3 × n=2 × n + n + 2 - 2
The picture below shows what triangular and quadrangular prisms made of glass look like.

Types of figure. Tilted prism
It has already been said above that the name of a prism is determined by the number of sides of the polygon at the base. However, there are other features in its structure that determine the properties of the figure. So, if all the parallelograms that form the lateral surface of the prism are represented by rectangles or squares, then such a figure is called a straight line. For a straight prism, the distance between the bases is equal to the length of the side edge of any rectangle.
If some or all of the sides are parallelograms, then we are talking about an inclined prism. Its height will already be less than the length of the side rib.
Another criterion by which the figures under consideration are classified is the lengths of the sides and the angles of the polygon at the base. If they are equal to each other, then the polygon will be correct. A straight figure with a regular polygon at the bases is called regular. It is convenient to work with it when determining the surface area and volume. An inclined prism in this regard presents some difficulties.
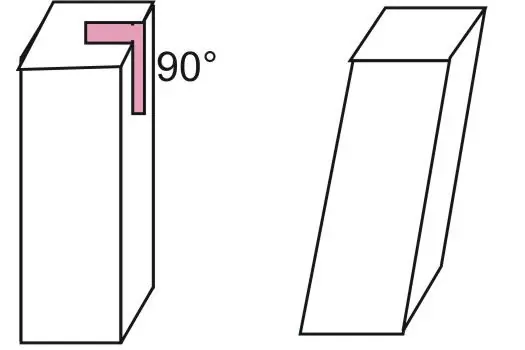
The figure below shows two prisms with a quadrangular base. The 90° angle shows the fundamental difference between a straight and oblique prism.
Formula for determining the volume of a figure
Part of space bounded by the faces of a prism is called its volume. For the considered figures of any type, this value can be determined by the following formula:
V=h × So
Here, the symbol h denotes the height of the prism,which is a measure of the distance between two bases. Symbol So- one base area.
The base area is easy to find. Given the fact whether the polygon is regular or not, and knowing the number of its sides, you should apply the appropriate formula and get So. For example, for a regular n-gon with side length a, the area will be:
S=n / 4 × a2 × ctg (pi / n)
Now let's move on to height h. For a straight prism, determining the height is not difficult, but for an oblique prism, this is not an easy task. It can be solved by various geometric methods, starting from specific initial conditions. However, there is a universal way to determine the height of a figure. Let's describe it briefly.
The idea is to find the distance from a point in space to a plane. Assume that the plane is given by the equation:
A × x+ B × y + C × z + D=0
Then from the point with coordinates (x1; y1; z1) will be at a distance:
h=|A × x1 + B × y1+ C × z1 +D| / √ (A2 + B2+ C2)
If the coordinate axes are arranged so that the point (0; 0; 0) lies in the plane of the lower base of the prism, then the equation for the base plane can be written as follows:
z=0
This means that the formula for the height will be writtenso:
h=z1
It is enough to find the z-coordinate of any point of the upper base to determine the height of the figure.
Example of problem solving
The figure below shows a quadrangular prism. The base of an inclined prism is a square with a side of 10 cm. It is necessary to calculate its volume if it is known that the length of the side edge is 15 cm, and the acute angle of the frontal parallelogram is 70 °.
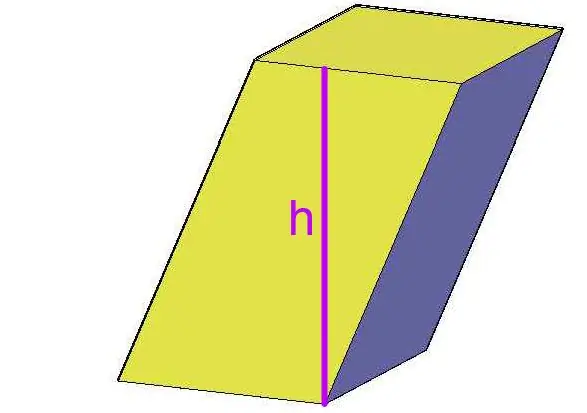
Since the height h of the figure is also the height of the parallelogram, we use formulas to determine its area to find h. Let's denote the sides of the parallelogram as follows:
a=10cm;
b=15cm
Then you can write the following formulas for it to determine the area Sp:
Sp=a × b × sin (α);
Sp=a × h
From where we get:
h=b × sin (α)
Here α is an acute angle of the parallelogram. Since the base is a square, the formula for the volume of an inclined prism will take the form:
V=a2 × b × sin (α)
We substitute the data from the condition into the formula and get the answer: V ≈ 1410 cm3.






