Formula for determining the volume of a cone. Problem solution example

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

Each student in the study of stereometry in high school came across a cone. Two important characteristics of this spatial figure are surface area and volume. In this article, we will show how to find the volume of a round cone.

Round cone as a figure of rotation of a right triangle

Before going directly to the topic of the article, it is necessary to describe the cone from a geometric point of view.

Let there be some right triangle. If you rotate it around any of the legs, then the result of this action will be the desired figure, shown in the figure below.

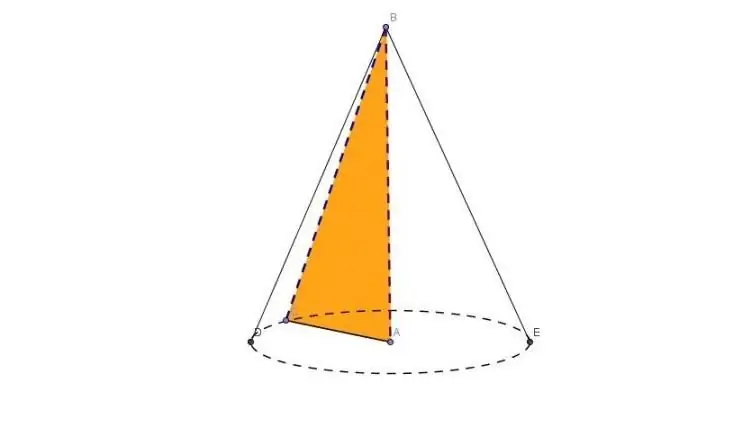
Here, leg AB is part of the axis of the cone, and its length corresponds to the height of the figure. The second leg (segment CA) will be the radius of the cone. During rotation, it will describe a circle that bounds the base of the figure. The hypotenuse BC is called the generatrix of the figure, or its generatrix. Point B is the only vertex of the cone.

Given the properties of the triangle ABC, we can write the relationship between the generatrix g, radius r and height h as followsequality:

g²=h²+ r²

This formula is useful in solving many geometric problems with the figure in question.

Cone volume formula

The volume of any spatial figure is the area of space, which is limited by the surfaces of this figure. There are two such surfaces for a cone:

1. Lateral, or conical. It is formed by all generatrices.
2. Foundation. In this case, it is a circle.

Get the formula for determining the volume of a cone. To do this, we mentally cut it into many layers parallel to the base. Each of the layers has a thickness dx, which tends to zero. The area S_xof the layer at a distance x from the top of the figure is equal to the following expression:

S_x=pir²x²/h ²

The correctness of this expression can be verified intuitively by substituting the values x=0 and x=h. In the first case, we will get an area equal to zero, in the second case, it will be equal to the area of the round base.

To determine the volume of the cone, you need to add up small "volumes" of each layer, that is, you should use the integral calculus:

V=∫₀^h(pir²x ²/h²dx)=pir²/h² ∫₀^h(x²dx)

Calculating this integral, we arrive at the final formula for a round cone:

V=1/3pir²h

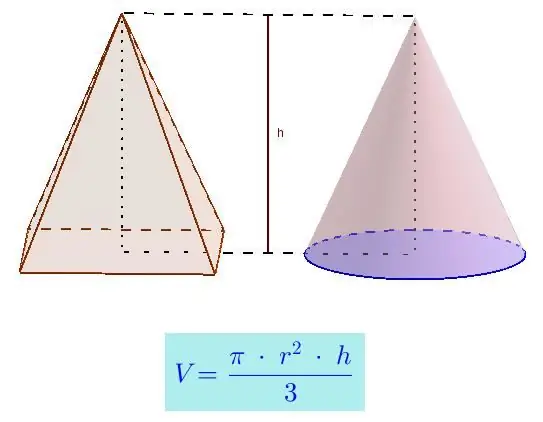
It is interesting to note that this formula is completely similar to the one used to calculate the volume of an arbitrary pyramid. This coincidence is not accidental, because any pyramid becomes a cone when the number of its edges increases to infinity.

Volume Calculation Problem

It is useful to give an example of solving the problem, which will demonstrate the use of the derived formula for the volume V.

Given a round cone whose base area is 37 cm², and the generator of the figure is three times the radius. What is the volume of the cone?

We have the right to use the volume formula if we know two quantities: the height h and the radius r. Let's find the formulas that determine them in accordance with the condition of the problem.

Radius r can be calculated by knowing the area of the circle S_o, we have:

S_o=pir²=>

r=√(S_o/pi)

Using the condition of the problem, we write the equality for the generator g:

g=3r=3√(S_o/pi)

Knowing the formulas for r and g, calculate the height h:

h=√(g²- r²)=√(9S_o /pi - S_o/pi)=√(8S_o/pi)

We found all the necessary parameters. Now it's time to plug them into the formula for V:

V=1/3pir²h=1/3piS_o/pi√ (8S_o/pi)=S_o/3√(8S_o /pi)

It remains to substitutebase area S_o and calculate the volume value: V=119.75 cm³.