Dihedral angles of the pyramid and the method of their calculation

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

Typical linear parameters of any pyramid are the lengths of the sides of its base, height, side edges and apothems. Nevertheless, there is another characteristic that is associated with the noted parameters - this is the dihedral angle. Consider in the article what it is and how to find it.

Spatial figure pyramid

Every student has a good idea of what is at stake when he hears the word "pyramid". It can be constructed geometrically as follows: select a certain polygon, then fix a point in space and connect it to each corner of the polygon. The resulting three-dimensional figure will be a pyramid of an arbitrary type. The polygon that forms it is called the base, and the point to which all its corners are connected is the vertex of the figure. The figure below schematically shows a pentagonal pyramid.

It can be seen that its surface is formed not only by a pentagon, but also by five triangles. In general, the number of these triangles will be equal to the numbersides of a polygonal base.

Dihedral angles of the figure

When geometric problems are considered on a plane, any angle is formed by two intersecting straight lines, or segments. In space, dihedral angles are added to these linear angles, formed by the intersection of two planes.

If the marked definition of an angle in space is applied to the figure in question, then we can say that there are two types of dihedral angles:

• At the base of the pyramid. It is formed by the plane of the base and any of the side faces (triangle). This means that the base angles of the pyramid are n, where n is the number of sides of the polygon.
• Between the sides (triangles). The number of these dihedral angles is also n pieces.

Note that the first type of considered angles is built on the edges of the base, the second type - on the side edges.

How to calculate the angles of a pyramid?

The linear angle of a dihedral angle is the measure of the latter. It is not easy to calculate it, since the faces of the pyramid, unlike the faces of the prism, do not intersect at right angles in the general case. It is most reliable to calculate the values of dihedral angles using the equations of the plane in general form.

In three-dimensional space, a plane is given by the following expression:

Ax + By + Cz + D=0

Where A, B, C, D are some real numbers. The convenience of this equation is that the first three marked numbers are the coordinates of the vector,which is perpendicular to the given plane, i.e.:

n¯=[A; B; C]

If the coordinates of three points belonging to the plane are known, then by taking the vector product of two vectors built on these points, one can obtain the coordinates n¯. The vector n¯ is called the guide for the plane.

According to the definition, the dihedral angle formed by the intersection of two planes is equal to the linear angle between their direction vectors. Suppose we have two planes whose normal vectors are equal:

₁¯=[A₁; B₁; C₁];

₂¯=[A₂; B₂; C₂]

To calculate the angle φ between them, you can use the scalar product property, then the corresponding formula becomes:

φ=arccos(|(n₁¯n₂¯)|/(|n₁ ¯||n₂¯|))

Or in coordinate form:

φ=arccos(|A₁A₂+ B₁B ₂+ C₁C₂|/(√(A₁ 2 ^{+ B}12^+C12 ^)√(A22 ^{+ B}22+ C²₂)))

Let's show how to use the above method for calculating dihedral angles when solving geometric problems.

Angles of a regular quadrangular pyramid

Assume that there is a regular pyramid, at the base of which there is a square with a side of 10 cm. The height of the figure is12 cm. It is necessary to calculate what the dihedral angles are at the base of the pyramid and for its sides.

Since the figure given in the condition of the problem is correct, that is, it has high symmetry, then all angles at the base are equal to each other. The angles formed by the side faces are also the same. To calculate the required dihedral angles, we find the direction vectors for the base and two side planes. Denote the length of the side of the base by the letter a, and the height h.

The picture above shows a quadrangular regular pyramid. Let's write out the coordinates of points A, B, C and D in accordance with the entered coordinate system:

A(a/2; -a/2; 0);

B(a/2; a/2; 0);

C(-a/2; a/2; 0);

D(0; 0; h)

Now let's find the direction vectors for the base planes ABC and the two sides ABD and BCD in accordance with the method described in the paragraph above:

For ABC:

AB¯=(0; a; 0); AC¯=(-a; a; 0); n₁¯=[AB¯AC¯]=(0; 0; a²)

For ABD:

AB¯=(0; a; 0); AD¯=(-a/2; a/2; h); n₂¯=[AB¯AD¯]=(ah; 0; a²/2)

For BCD:

BC¯=(-a; 0; 0); BD¯=(-a/2; -a/2; h); n₃¯=[BC¯BD¯]=(0; ah; a²/2)

Now it remains to apply the appropriate formula for the angle φ and substitute the side and height values from the problem statement:

Angle between ABC andABD:

(n₁¯n₂¯)=a⁴/2; |n₁¯|=a²; |n₂¯|=a√(h² + a²/4);

φ=arccos(a⁴/2/(a²a√(h^{2+ a}2^{/4)))=arccos(a/(2√(h}2 ^{+ a}2 /4)))=67, 38^o

Angle between ABD and BDC:

(n₂¯n₃¯)=a⁴/4; |n₂¯|=a√(h² + a²/4); |n₃¯|=a√(h² + a²/4);

φ=arccos(a⁴/(4a²(h²+ a²/4))=arccos(a²/(4(h²+a 2^{/4)))=81, 49}o

We calculated the values of the angles that needed to be found by the condition of the problem. The formulas obtained in solving the problem can be used to determine the dihedral angles of quadrangular regular pyramids with any values of a and h.

Angles of a triangular regular pyramid

The figure below shows a pyramid whose base is a regular triangle. It is known that the dihedral angle between the sides is right. It is necessary to calculate the area of \u200b\u200bthe base if it is known that the height of the figure is 15 cm.

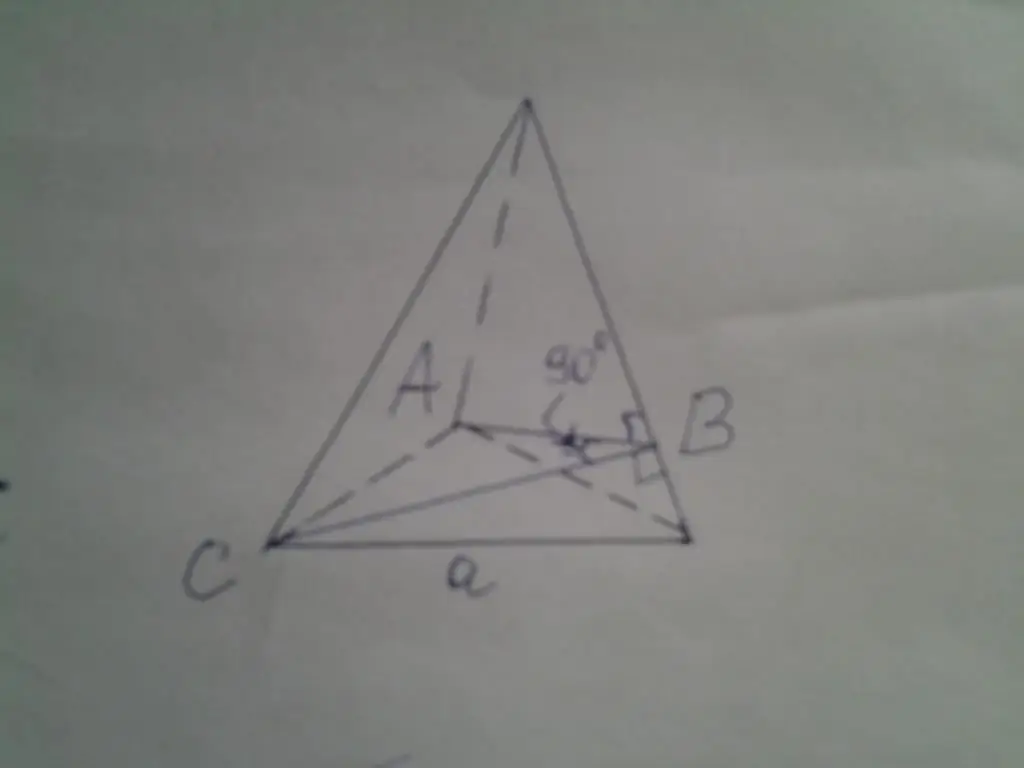
A dihedral angle equal to 90^o is denoted as ABC in the figure. You can solve the problem using the above method, but in this case we will do it easier. Let's denote the side of the triangle a, the height of the figure - h, the apothema - h_b and the siderib - b. Now you can write the following formulas:

S=1/2ah_b;

b²=h_b²+ a² /4;

b²=h² + a²/3

Since the two side triangles in the pyramid are the same, the sides AB and CB are equal and are the legs of the triangle ABC. Let's denote their length by x, then:

x=a/√2;

S=1/2ba/√2

Equiting the areas of the side triangles and substituting the apothem into the corresponding expression, we have:

1/2ah_b=1/2ba/√2=>

h_b=b/√2;

b²=b ²/2 + a²/4=>

b=a/√2;

a²/2=h² + a²/3=>

a=h√6

The area of an equilateral triangle is calculated as follows:

S=√3/4a²=3√3/2h²

Substitute the height value from the condition of the problem, we get the answer: S=584, 567 cm².