Quadric equations often appear in a number of problems in mathematics and physics, so every student should be able to solve them. This article details the main methods for solving quadratic equations, and also provides examples of their use.
What equation is called quadratic
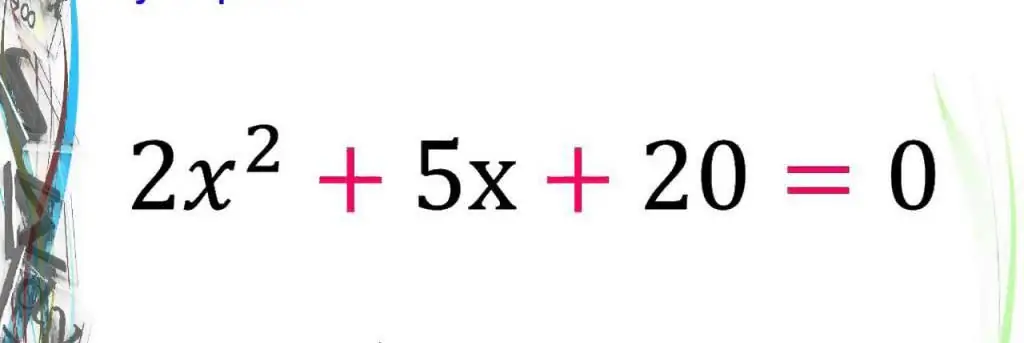
First of all, we will answer the question of this paragraph in order to better understand what the article will be about. So, the quadratic equation has the following general form: c + bx+ax2=0, where a, b, c are some numbers, which are called coefficients. Here a≠0 is a mandatory condition, otherwise the indicated equation degenerates into a linear one. The remaining coefficients (b, c) can take absolutely any values, including zero. Thus, expressions like ax2=0, where b=0 and c=0, or c+ax2=0, where b=0, or bx+ax2=0, where c=0 are also quadratic equations, which are called incomplete, since either the linear coefficient b in them is zero or zerois a free term c, or they both vanish.
An equation in which a=1 is called reduced, that is, it has the form: x2 + с/a + (b/a)x=0.
The solution of a quadratic equation is to find such x values that satisfy its equality. These values are called roots. Since the equation under consideration is an expression of the second degree, this means that the maximum number of its roots cannot exceed two.
What methods for solving square equations exist
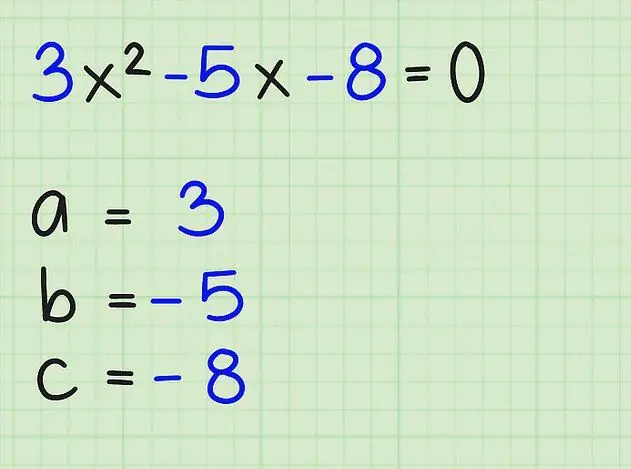
In general, there are 4 solution methods. Their names are listed below:
- Factoring.
- Addition to the square.
- Using a known formula (via the discriminant).
- The solution method is geometric.
As you can see from the above list, the first three methods are algebraic, so they are used more often than the last one, which involves plotting a function.
There is another way to solve square equations using the Vieta theorem. It could be included 5th in the list above, however, this is not done, since Vieta's theorem is a simple consequence of the 3rd method.
Later in the article we will consider in more detail the named methods of solution, and also give examples of their use to find the roots of specific equations.
Method 1. Factoring
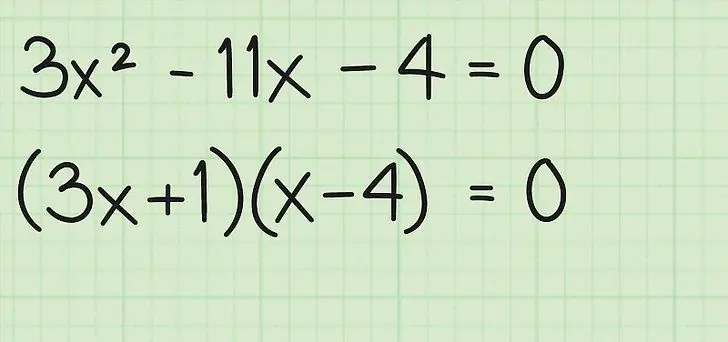
For this method in the mathematics of quadratic equations, there is a beautifulname: factorization. The essence of this method is as follows: it is necessary to present the quadratic equation as a product of two terms (expressions), which should be equal to zero. After such a representation, you can use the product property, which will be equal to zero only when one or more (all) of its members are zero.
Now consider the sequence of specific actions that need to be performed to find the roots of the equation:
- Move all members to one part of the expression (for example, to the left) so that only 0 remains in its other part (right).
- Represent the sum of the terms in one part of the equation as a product of two linear equations.
- Set each of the linear expressions to zero and solve them.
As you can see, the factorization algorithm is quite simple, however, most students have difficulties during the implementation of the 2nd point, so we will explain it in more detail.
To guess which 2 linear expressions, when multiplied by each other, will give the desired quadratic equation, you need to remember two simple rules:
- The linear coefficients of two linear expressions, when multiplied by each other, should give the first coefficient of the quadratic equation, that is, the number a.
- The free terms of linear expressions, when multiplied, should give the number c of the desired equation.
After all the numbers of factors are selected, they should be multiplied, and if they give the desired equation, then go to step 3 inthe above algorithm, otherwise you should change the multipliers, but you need to do this so that the above rules are always followed.
Example of solution by factorization method
Let's show clearly how the algorithm for solving a quadratic equation is to compose and find unknown roots. Let an arbitrary expression be given, for example, 2x-5+5x2-2x2=x2 +2+x2+1. Let's move on to its solution, observing the sequence of points from 1 to 3, which are set out in the previous paragraph of the article.
Item 1. Move all the terms to the left side and arrange them in the classical sequence for a quadratic equation. We have the following equality: 2x+(-8)+x2=0.
Item 2. We break it into a product of linear equations. Since a=1, and c=-8, then we will select, for example, such a product (x-2)(x+4). It satisfies the rules for finding the expected factors set out in the paragraph above. If we open the brackets, we get: -8+2x+x2, that is, we get exactly the same expression as on the left side of the equation. This means that we correctly guessed the multipliers, and we can proceed to the 3rd step of the algorithm.
Item 3. Equate each factor to zero, we get: x=-4 and x=2.
If there are any doubts about the result, it is recommended to check by substituting the found roots into the original equation. In this case, we have: 22+22-8=0 and 2(-4)+(-4)2-8=0. Roots found correctly.
Thus, using the factorization method, we found that the given equation has two roots of differenthas: 2 and -4.
Method 2. Complement to the full square
In the algebra of square equations, the multiplier method cannot always be used, since in the case of fractional values of the coefficients of the quadratic equation, difficulties arise in the implementation of paragraph 2 of the algorithm.
The full square method, in turn, is universal and can be applied to quadratic equations of any type. Its essence is to perform the following operations:
- The terms of the equation containing the coefficients a and b must be transferred to one part of the equation, and the free term c to the other.
- Next, the parts of the equality (right and left) should be divided by the coefficient a, that is, present the equation in the above form (a=1).
- Sum the terms with coefficients a and b to represent as a square of a linear equation. Since a \u003d 1, then the linear coefficient will be equal to 1, as for the free term of the linear equation, then it should be equal to half the linear coefficient of the reduced quadratic equation. After the square of the linear expression has been drawn up, it is necessary to add the corresponding number to the right side of the equality, where the free term is located, which is obtained by expanding the square.
- Take the square root with "+" and "-" signs and solve the linear equation already obtained.
The described algorithm may at first glance be perceived as rather complicated, however, in practice it is easier to implement than the factorization method.
An example of a solution using the full square complement
Let's give an example of a quadratic equation for training its solution by the method described in the previous paragraph. Let the quadratic equation -10 - 6x+5x2=0 be given. We begin to solve it following the algorithm described above.
Item 1. We use the transfer method when solving square equations, we get: - 6x+5x2=10.
Point 2. The reduced form of this equation is obtained by dividing by the number 5 of each of its members (if both parts are divided or multiplied by the same number, then the equality will be preserved). As a result of the transformations, we get: x2 - 6/5x=2.
Item 3. Half of the coefficient - 6/5 is equal to -6/10=-3/5, use this number to complete the square, we get: (-3/5+x)2 . We expand it and the resulting free term should be subtracted from the left side of the equality in order to satisfy the original form of the quadratic equation, which is equivalent to adding it to the right side. As a result, we get: (-3/5+x)2=59/25.
Item 4. Calculate the square root with positive and negative signs and find the roots: x=3/5±√59/5=(3±√59)/5. The two found roots have the following values: x1=(√59+3)/5 and x1=(3-√59)/5.
Since the calculations performed are related to roots, there is a high probability of making a mistake. Therefore, it is recommended to check the correctness of the roots x2 and x1. We get for x1: 5((3+√59)/5)2-6(3+√59)/5 - 10=(9+59+6√59)/5 - 18/5 - 6√59/5-10=68/5-68/5=0. Substitute nowx2: 5((3-√59)/5)2-6(3-√59)/5 - 10=(9+59-6√59)/5 - 18/5 + 6√59/5-10=68/5-68/5=0.
Thus, we have shown that the found roots of the equation are true.
Method 3. Application of the well-known formula
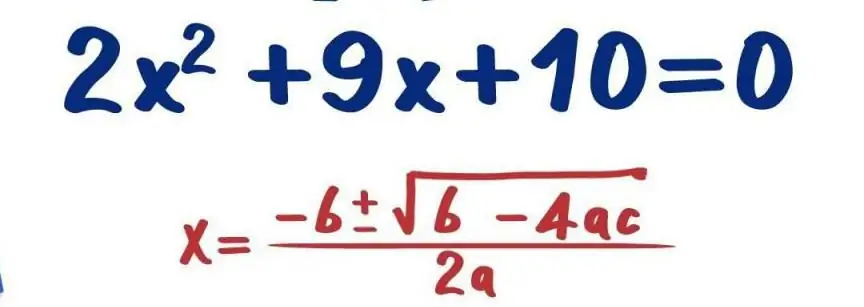
This method of solving quadratic equations is perhaps the simplest, since it consists in substituting the coefficients into a known formula. To use it, you do not need to think about compiling solution algorithms, it is enough to remember only one formula. It is shown in the picture above.
In this formula, the radical expression (b2-4ac) is called the discriminant (D). From its value depends on what roots are obtained. There are 3 cases:
- D>0, then the root two equation has real and different ones.
- D=0, then one gets the root, which can be calculated from the expression x=-b/(a2).
- D<0, then you get two different imaginary roots, which are represented as complex numbers. For example, the number 3-5i is complex, while the imaginary unit i satisfies the property: i2=-1.
An example of a solution by calculating the discriminant
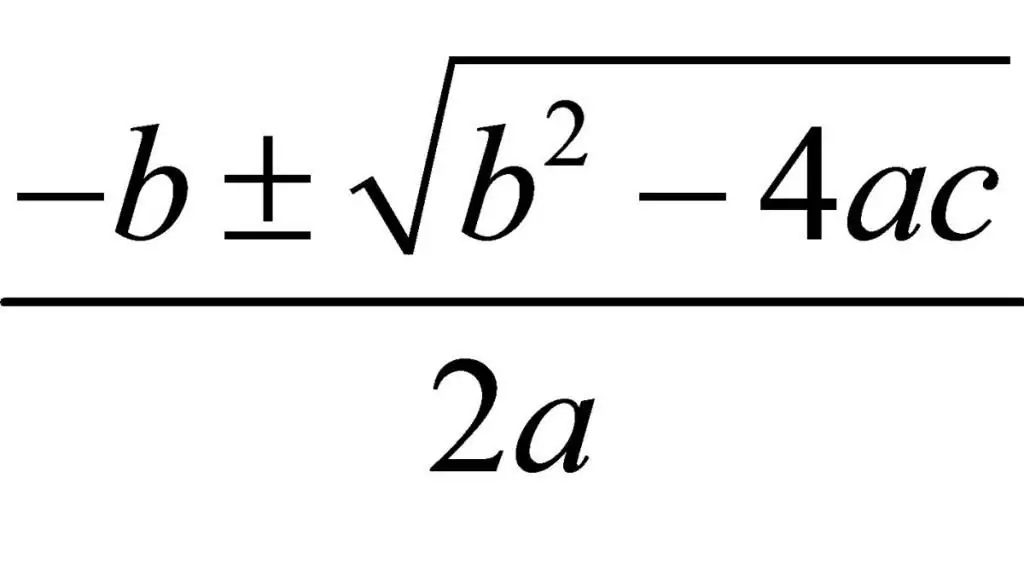
Let's give an example of a quadratic equation to practice using the above formula. Find the roots for -3x2-6+3x+4x=0. First, calculate the value of the discriminant, we get: D=b2 -4ac=72-4(-3)(-6)=-23.
Since D<0 is obtained, it means that the roots of the considered equation are complex numbers. Let's find them by substituting the found value D into the formula given in the previous paragraph (it is also shown in the photo above). We get: x=7/6±√(-23)/(-6)=(7±i√23)/6.
Method 4. Using the Function Graph
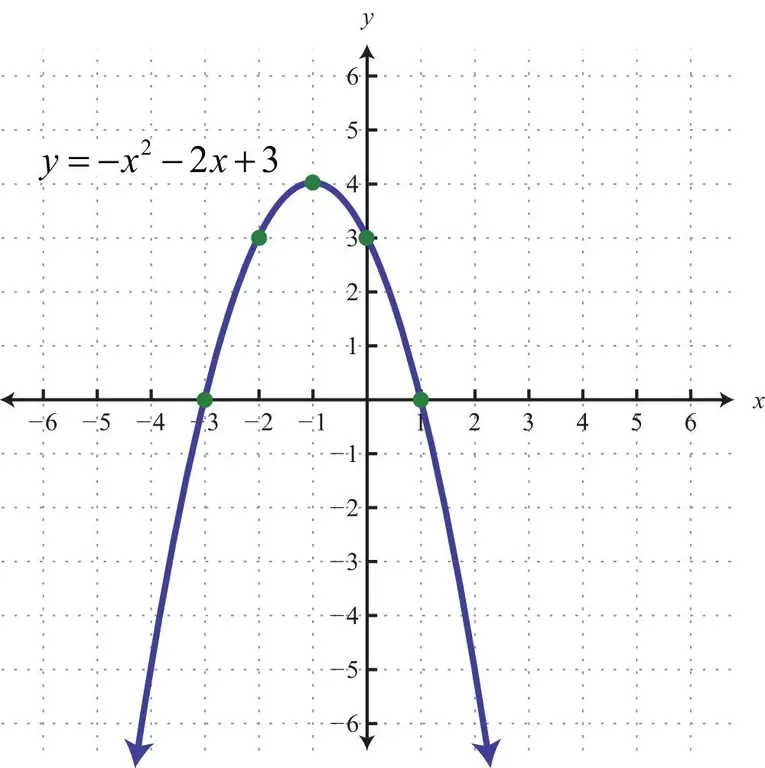
It is also called the graphical method for solving square equations. It should be said that, as a rule, it is used not for quantitative, but for qualitative analysis of the equation under consideration.
The essence of the method is to plot a quadratic function y=f(x), which is a parabola. Then, it is necessary to determine at what points the parabola intersects the x-axis (X), they will be the roots of the corresponding equation.
To tell if a parabola will intersect the X axis, it is enough to know the position of its minimum (maximum) and the direction of its branches (they can either increase or decrease). There are two properties of this curve to remember:
- If a>0 - the parabolas of the branch are directed upwards, on the contrary, if a<0, then they go down.
- The minimum (maximum) coordinate of a parabola is always x=-b/(2a).
For example, you need to determine if the equation has roots -4x+5x2+10=0. The corresponding parabola will be directed upwards, since a=5>0. Its extremum has coordinates: x=4/10=2/5, y=-42/5+5(2/5)2+10=9, 2. Since the minimum of the curve lies above the x-axis (y=9, 2), then it does not intersect the latter for anyx values. That is, the given equation has no real roots.

Vieta's theorem
As noted above, this theorem is a consequence of method No. 3, which is based on the application of a formula with a discriminant. The essence of the Vieta theorem is that it allows you to connect the coefficients of the equation and its roots into equality. Let's get the corresponding equalities.
Let's use the formula for calculating the roots through the discriminant. Add two roots, we get: x1+x2=-b/a. Now let's multiply the roots by each other: x1x2, after a series of simplifications we get the number c/a.
Thus, to solve the quadratic equations by the Vieta theorem, you can use the obtained two equalities. If all three coefficients of an equation are known, then the roots can be found by solving the appropriate system of these two equations.
An example of using Vieta's theorem
You need to write a quadratic equation if you know that it has the form x2+c=-bx and its roots are 3 and -4.
Since a=1 in the equation under consideration, the Vieta formulas will look like: x2+x1=-b and x 2x1=p. Substituting the known values of the roots, we get: b=1 and c=-12. As a result, the restored quadratic reduced equation will look like: x2-12=-1x. You can substitute the value of the roots into it and make sure that the equality holds.
Reverse application of the Vieta theorem, that is, the calculation of the roots byknown form of the equation, allows for small integers a, b and c to quickly (intuitively) find solutions.






