Properties and methods for finding the roots of a quadratic equation

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

The world is arranged in such a way that the solution of a large number of problems comes down to finding the roots of a quadratic equation. The roots of equations are important for describing various patterns. This was known even to the surveyors of ancient Babylon. Astronomers and engineers were also forced to solve such problems. Back in the 6th century AD, the Indian scientist Aryabhata developed the basics for finding the roots of a quadratic equation. The formulas were completed in the 19th century.

General concepts

We suggest that you familiarize yourself with the basic regularities of quadratic equalities. In general, equality can be written as follows:

ax2 + bx + c=0, The number of roots of a quadratic equation can be equal to one or two. A quick analysis can be done using the concept of discriminant:

D=b2 - 4ac

Depending on the calculated value, we get:

• When D > 0 there are two different roots. The general formula for determining the roots of a quadratic equation looks like (-b± √D) / (2a).
• D=0, in this case the root is one and corresponds to the value x=-b / (2a)
• D < 0, for a negative value of the discriminant, there is no solution to the equation.

Note: if the discriminant is negative, the equation has no roots only in the region of real numbers. If algebra is extended to the concept of complex roots, then the equation has a solution.

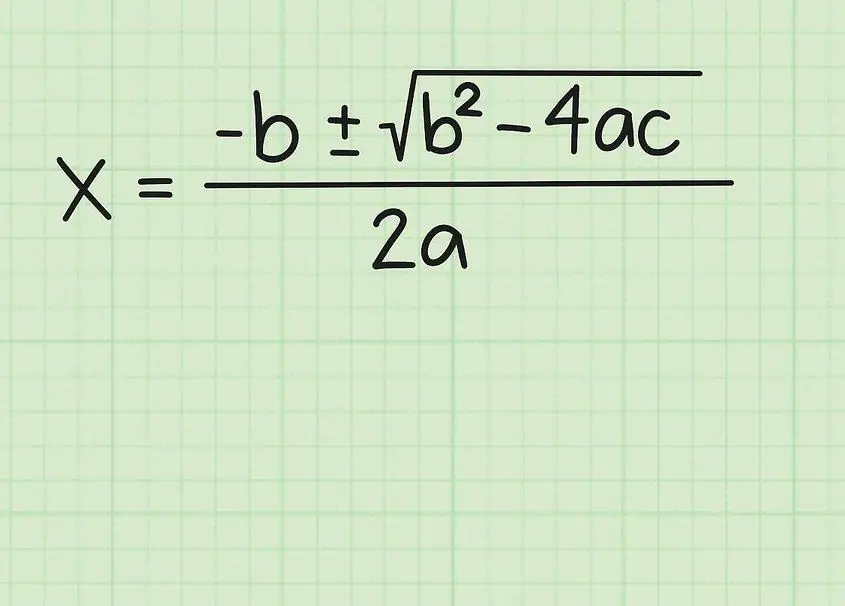
Let's give a chain of actions that confirms the formula for finding roots.

From the general form of the equation, it follows:

ax2 + bx=-c

We multiply the right and left parts by 4a and add b2, we get

4a²x² + 4abx + b² =-4ac+b ²

Transform the left side into the square of the polynomial (2ax + b)². We extract the square root of both sides of the equation 2ax + b=-b ± √(-4ac + b^{2), transfer the coefficient b to the right side, we get:}

2ax=-b ± √(-4ac + b2)

From here follows:

x=(-b ± √(b2 - 4ac))

What was required to show.

Special case

In some cases, the solution of the problem can be simplified. So, for an even coefficient b we get a simpler formula.

Denote k=1/2b, then the formula of the general form of the roots of the quadratic equation takes the form:

x=(-k ± √(k2 -ac)) / a

When D=0, we get x=-k / a

Another special case is the solution of the equation with a=1.

For the form x² + bx + c=0 the roots will be x=-k ± √(k^{2 - c) with discriminant greater than 0. For the case when D=0, the root will be determined by a simple formula: x=-k.}

Use charts

Any person, without even knowing it, is constantly faced with physical, chemical, biological and even social phenomena that are well described by a quadratic function.

Note: the curve built on the basis of a quadratic function is called a parabola.

Here are some examples.

1. When calculating the trajectory of a projectile, the property of movement along a parabola of a body fired at an angle to the horizon is used.
2. The property of a parabola to evenly distribute the load is widely used in architecture.

Understanding the importance of the parabolic function, let's figure out how to use the graph to explore its properties, using the concepts of "discriminant" and "roots of a quadratic equation".

Depending on the value of the coefficients a and b, there are only six options for the position of the curve:

1. The discriminant is positive, a and b have different signs. The branches of the parabola look up, the quadratic equation has two solutions.
2. Discriminant and coefficient b are equal to zero, coefficient a is greater than zero. The graph is in the positive zone, the equation has 1 root.
3. The discriminant and all coefficients are positive. The quadratic equation has no solution.
4. Discriminant and coefficient a are negative, b is greater than zero. The branches of the graph are directed downwards, the equation has two roots.
5. Discriminant andcoefficient b are equal to zero, coefficient a is negative. The parabola looks down, the equation has one root.
6. The values of the discriminant and all coefficients are negative. There are no solutions, the function values are completely in the negative zone.

Note: the option a=0 is not considered, since in this case the parabola degenerates into a straight line.

All of the above is well illustrated by the figure below.

Examples of problem solving

Condition: using the general properties, make a quadratic equation whose roots are equal to each other.

Solution:

according to the condition of the problem x₁ =x₂, or -b + √(b² - 4ac) / (2a)=-b + √(b^{2 - 4ac) / (2a). Simplifying the notation:}

-b + √(b² - 4ac) / (2a) - (-b - √(b² - 4ac) / (2a))=0, open the brackets and give like terms. The equation becomes 2√(b² - 4ac)=0. This statement is true when b² - 4ac=0, hence b ^{2=4ac, then the value b=2√(ac) is substituted into the equation}

ax² + 2√(ac)x + c=0, in the reduced form we get x^{2 + 2√(c / a)x + c=0.}

Answer:

for a not equal to 0 and any c, there is only one solution if b=2√(c / a).

Quadric equations, for all their simplicity, are of great importance in engineering calculations. Almost any physical process can be described with some approximation usingpower functions of order n. The quadratic equation will be the first such approximation.