Gases, from the point of view of thermodynamics, are described by a set of macroscopic characteristics, the main of which are temperature, pressure and volume. The constancy of one of these parameters and the change in the other two indicates that one or another isoprocess occurs in the gas. We will devote this article to a detailed answer to the questions that this is an isochoric process, how it differs from isothermal and isobaric changes in the states of a gas system.
Ideal gas in physics

Before answering the question that this is an isochoric process, you should get to know the concept of an ideal gas better. In physics, it is understood as any gas in which the average kinetic energy of its constituent particles far exceeds the potential energy of their interaction, and the distances between these particles are several orders of magnitude larger than their linear dimensions. Under the noted conditions, it is possible, when carrying outcalculations do not take into account the energy of interaction between particles (it is equal to zero), and it can also be assumed that particles are material points having a certain mass m.
The only process that takes place in an ideal gas is the collision of particles with the walls of the vessel containing the substance. These collisions manifest themselves in practice as the existence of a certain pressure in the gas P.
As a rule, any gaseous substance that consists of relatively chemically inert molecules and that has low pressure and high temperatures can be considered an ideal gas with sufficient accuracy for practical calculations.
Equation describing an ideal gas
Of course, we are talking about the universal law of Clapeyron-Mendeleev, which should be well understood in order to understand that this is an isochoric process. So, the universal equation of state has the following form:
PV=nRT.
That is, the product of the pressure P and the gas volume V is equal to the product of the absolute temperature T and the amount of substance in moles n, where R is the proportionality factor. The equation itself was first written down by Emile Clapeyron in 1834, and in the 70s of the 19th century, D. Mendeleev replaced in it a set of constant values of a single universal gas constant R (8.314 J/(molK)).
In accordance with the Clapeyron-Mendeleev equation, in a closed system the number of gas particles remains constant, so there are only three macroscopic parameters that can change (T, Pand V). The latter fact underlies the understanding of the various isoprocesses that will be discussed below.
What is an isochoric process?
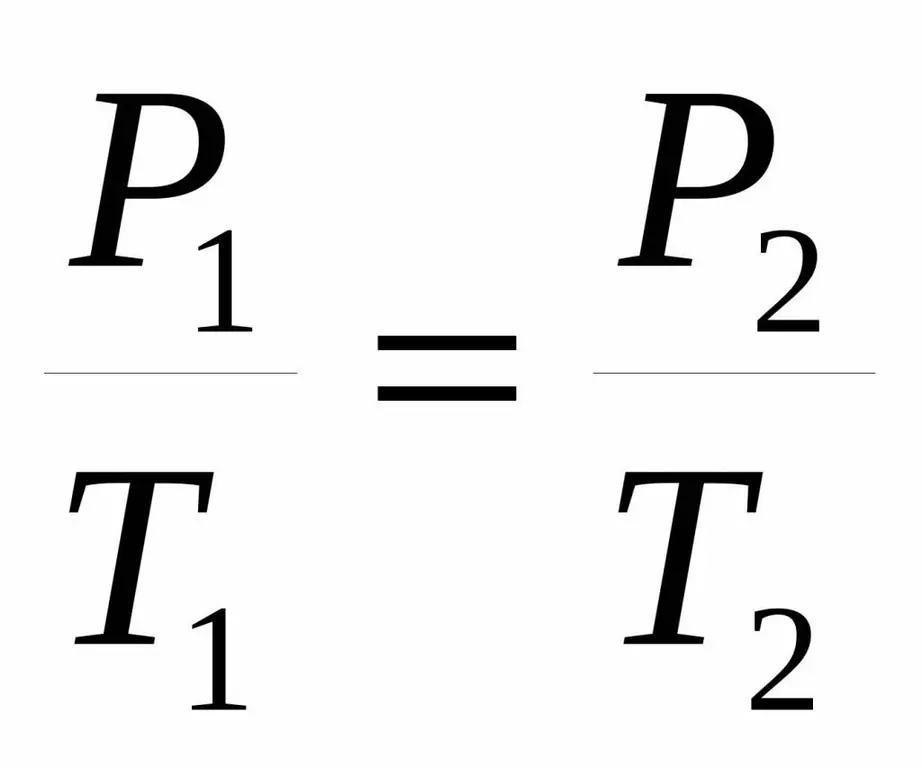
This process is understood as absolutely any change in the state of the system, in which its volume is preserved.
If we turn to the universal equation of state, we can say that in an isochoric process only pressure and absolute temperature change in a gas. To understand exactly how the thermodynamic parameters change, we write the corresponding mathematical expression:
P / T=const.
Sometimes this equality is given in a slightly different form:
P1 / T1=P2 / T 2.
Both equalities are called Charles' law after the name of a French scientist who at the end of the 18th century obtained the noted dependence experimentally.

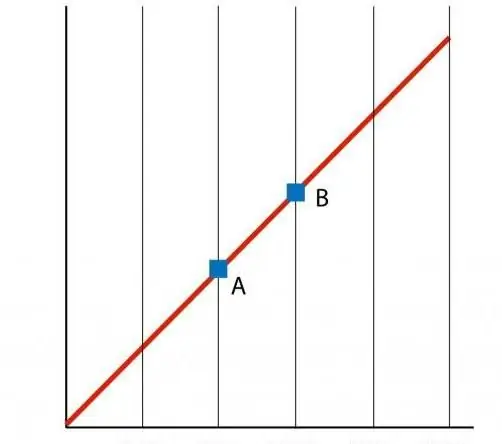
If we build a graph of the function P(T), then we get a straight-line dependence, which is called an isochore. Any isochore (for all values of n and V) is a straight line.
Energy description of the process
As noted, an isochoric process is a change in the state of a system that takes place in a closed but not isolated system. We are talking about the possibility of heat exchange between the gas and the environment. In general, any supply of heat Q to the system leads to two results:
- changes internal energy U;
- gasdoes work A, expanding or contracting.
The last inference is written mathematically as follows:
Q=U + A.
The isochoric process of an ideal gas, by its definition, does not imply work done by the gas, since its volume remains unchanged. This means that all the heat supplied to the system goes to increase its internal energy:
Q=U.
If we substitute the explicit formula for internal energy into this expression, then the heat of the isochoric process can be represented as:
Q=z / 2nRT.
Here z is the number of degrees of freedom, which is determined by the polyatomic nature of the molecules that make up the gas. For a monatomic gas, z=3, for a diatomic gas - 5, and for a triatomic and more - 6. Here, under the degrees of freedom, we mean translational and rotational degrees.
If we compare the efficiency of heating a gas system in isochoric and isobaric processes, then in the first case we will get the maximum efficiency, since during the isobaric change in the state of the system, the gas expands, and part of the heat input is spent on doing work.
Isobaric process
Above we have described in detail that this is an isochoric process. Now let's say a few words about other isoprocesses. Let's start with isobaric. Based on the name, it is understood as the transition of the system between states at constant pressure. This process is described by the Gay-Lussac law as follows:
V / T=const.
As with the isochore, the V(T) isobar also represents a straight line on the graph.
Forof any isobaric process, it is convenient to calculate the work done by the gas, since it is equal to the product of constant pressure and the change in volume.
Isothermal process
This is a process in which the temperature of the system remains constant. It is described by the Boyle-Mariotte law for an ideal gas. It is curious to note that this is the first experimentally discovered gas law (second half of the 17th century). Its mathematical notation looks like this:
PV=const.
Isochoric and isothermal processes differ in terms of their graphical representation, since the P(V) function is a hyperbolic, not a linear relationship.
Example of problem solving
Let's consolidate the theoretical information provided in the article by their application to solve a practical problem. It is known that pure gaseous nitrogen was in a cylinder at a pressure of 1 atmosphere and a temperature of 25 °C. After the gas cylinder was heated and the pressure in it was measured, it turned out to be 1.5 atmospheres. What is the temperature of the gas in the cylinder after heating? By what amount did the internal energy of the gas change if there were 4 moles of nitrogen in the balloon.
To answer the first question, we use the following expression:
P1 / T1=P2 / T 2.
From where we get:
T2=P2 / P1 T 1.
In this expression, pressure can be substituted in arbitrary unitsmeasurements, since they are shrinking, and the temperature is only in kelvins. With that said, we get:
T2=1.5 /1298.15=447.224 K.
The calculated temperature in degrees Celsius is 174 °C.
Since the nitrogen molecule is diatomic, the change in its internal energy during heating can be determined as follows:
ΔU=5 / 2nRΔT.
Substituting the known values into this expression, we will get the answer to the second question of the problem: ΔU=+12.4 kJ.






