In thermodynamics, when studying transitions from the initial to the final state of a system, it is important to know the thermal effect of the process. The concept of heat capacity is closely related to this effect. In this article, we will consider the question of what is meant by the isochoric heat capacity of a gas.
Ideal gas
An ideal gas is a gas whose particles are considered to be material points, that is, they do not have dimensions, but have mass, and in which all internal energy consists solely of the kinetic energy of the movement of molecules and atoms.
Any real gas ideally will never satisfy the described model, since its particles still have some linear dimensions and interact with each other using weak van der Waals bonds or chemical bonds of another type. However, at low pressures and high temperatures, the distances between molecules are large, and their kinetic energy exceeds the potential energy by dozens of times. All this makes it possible to apply the ideal model to real gases with a high degree of accuracy.
Internal energy of gas
The internal energy of any system is a physical characteristic, which is equal to the sum of potential and kinetic energy. Since potential energy can be neglected in ideal gases, we can write the equality for them:
U=Ek.
Where Ek is the energy of the kinetic system. Using the molecular kinetic theory and applying the universal Clapeyron-Mendeleev equation of state, it is not difficult to obtain an expression for U. It is written below:
U=z/2nRT.
Here T, R and n are the absolute temperature, the gas constant and the amount of substance, respectively. The z-value is an integer indicating the number of degrees of freedom that a gas molecule has.
Isobaric and isochoric heat capacity
In physics, heat capacity is the amount of heat that must be provided to the system under study in order to heat it by one kelvin. The reverse definition is also true, that is, the heat capacity is the amount of heat that the system releases when cooled by one kelvin.
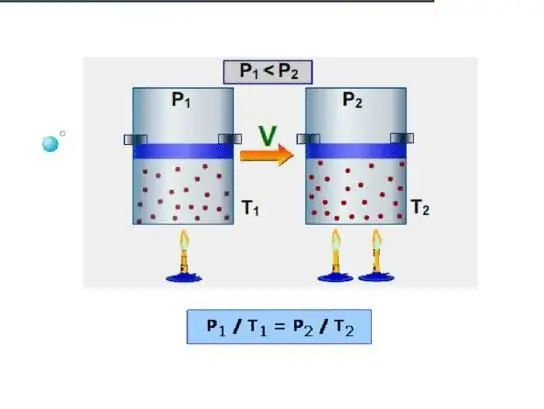
The easiest way for a system is to determine the isochoric heat capacity. It is understood as the heat capacity at constant volume. Since the system does not perform work under such conditions, all energy is spent on increasing internal energy reserves. Let us denote the isochoric heat capacity by the symbol CV, then we can write:
dU=CVdT.
That is, the change in internal energysystem is directly proportional to the change in its temperature. If we compare this expression with the equality written in the previous paragraph, then we arrive at the formula for CV in an ideal gas:
СV=z/2nR.
This value is inconvenient to use in practice, since it depends on the amount of substance in the system. Therefore, the concept of specific isochoric heat capacity was introduced, that is, a value that is calculated either per 1 mol of gas or per 1 kg. Denote the first value by the symbol CV, the second - by the symbol CVm. For them, you can write the following formulas:
CV=z/2R;
CVm=z/2R/M.
Here M is the molar mass.
Isobaric is the heat capacity while maintaining a constant pressure in the system. An example of such a process is the expansion of gas in a cylinder under a piston when it is heated. Unlike the isochoric process, during the isobaric process, the heat supplied to the system is spent to increase the internal energy and to perform mechanical work, that is:
H=dU + PdV.
The enthalpy of an isobaric process is the product of the isobaric heat capacity and the change in temperature in the system, that is:
H=CPdT.
If we consider the expansion at a constant pressure of 1 mol of gas, then the first law of thermodynamics will be written as:
CPdT=CV dT + RdT.
The last term is obtained from the equationClapeyron-Mendeleev. From this equality follows the relationship between isobaric and isochoric heat capacities:
CP=CV + R.
For an ideal gas, the specific molar heat capacity at constant pressure is always greater than the corresponding isochoric characteristic by R=8, 314 J/(molK).
Degrees of freedom of molecules and heat capacity
Let's write again the formula for the specific molar isochoric heat capacity:
CV=z/2R.
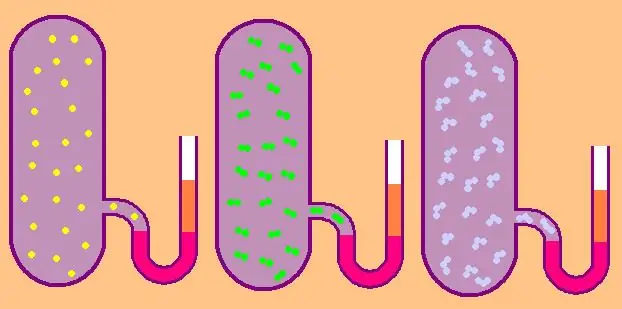
In the case of a monatomic gas, the value z=3, since atoms in space can only move in three independent directions.
If we are talking about a gas consisting of diatomic molecules, for example, oxygen O2 or hydrogen H2, then, in addition to translational motion, these molecules can still rotate around two mutually perpendicular axes, that is, z will be equal to 5.
For more complex molecules, use z=6. to determine CV






