A linear function is a straight line drawn along a surface. It can be divided into different types and models. Below we will consider the formulas for obtaining it, as well as achieving its perfection in the plane. In the drawings, you can fully verify this and understand how it should look.
Linear function y=kx + b
This value is an accurate measure of a variable in one view. Increment refers to the basic property of a linear function, it becomes proportional to the incremented argument. In other words, the function represents a generalization of direct proportionality. A straight line is a graph of a linear function. This is where its name comes from. One real variable touches another real function.
Properties
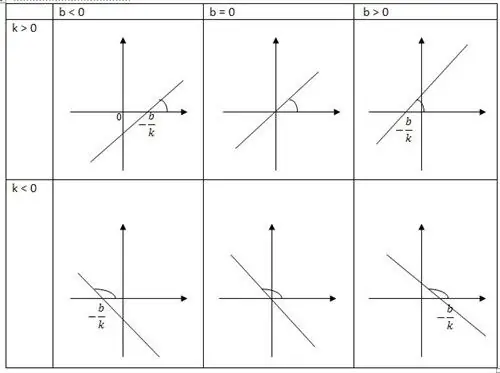
Linear function is a generatrix of a straight line, which has a positive direction of the x-axis. One of its defining slope factors is k, it determines the tangent of the angle a. The straight line formed in the positive direction of the x-axis is k. The other coordinate b indicatespoint coordinates, as well as the intersection of the line with the axis.
What are non-linear functions?
Functions that are not linear are called non-linear. This is a mathematical relationship between variables. Nonlinear ones cannot be expressed as y=ax + b. This term is used in those moments when it is necessary to study the general case. This process begins with the lower degrees. In this case, quadratic corrections are considered. Such a function has continuous curvature.
The considered non-linear equation is arbitrary. An example of a non-linear function is y=x2. The terms "linear function" are often used, with a refinement and the addition of "homogeneous". It can be applied to an exact linear mapping of X, which is a vector space. A linear function is the whole system like it.






