The older the students get, the more there is a need for speed in solving simple problems. Not much time is given in exams to solve simple examples or problems for a long time. How to find the diagonal of a square quickly and easily? This is taught to children from the eighth grade. This article shows two ways - one is longer, the other is faster.
How to calculate the diagonal of a square?
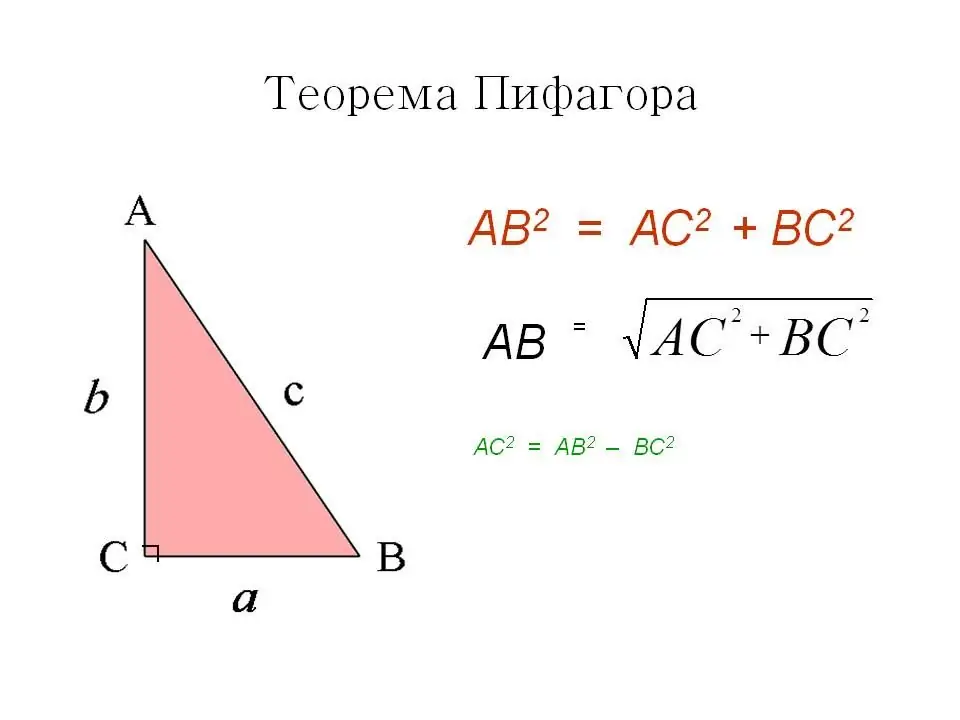
The first way is the well-known and familiar Pythagorean theorem. In a square, all angles are right, which means that the diagonal divides it into two equal right-angled triangles and is itself their hypotenuse. According to the Pythagorean theorem, the square of the hypotenuse is equal to the sum of the squares of the legs.

The second way is a simple formula that is unique to squares, and you just need to remember it. As you know, all sides of a square are equal, and that is why mathematicians have calculated the following formula for finding its diagonal: it is equal to the product of the side and the root of two.
Of course, it's best to just remember the formula for the length of the diagonal of a square and use it always, because it's much faster and more convenient. This is especially felt when solving problems in literal form, where instead of whole large root expressions, you can get by with only one product.
Example
Take, for example, a 6 by 6 square, that is, with a side equal to six centimeters.
According to the first method: let the diagonal be C, and the side be A.
Then we get that C=√A^2+A^2 or C=√2A^2.
Let's write it in numerical form: С=√36 + 36. We got √72, which is 3√8 or 6√2.
And now let's find the same diagonal, but by the second method: C=A√2 or in numerical form: 6√2
Now you can see how much the second method is faster, easier and most importantly - more efficient, especially in such easy problems, because every minute is precious in the exam!
Other properties of square diagonals
Besides knowing how to find the diagonals of a square, you also need to know their properties. The main ones are:
- The diagonals are equal to each other and the intersection point is divided in half.
- They form right angles when they intersect.
- Divide the square into equal triangles.
Conclusion
The question of how to count the diagonals of a square is usually asked by students who missed this topic at school. However, everyone should know such fundamental rules of mathematics! It is desirable to solve as quickly as possible, and this requires knowledge of abbreviated formulas. All this is extremely simple and easy, butat the same time, it is the basis necessary for solving much more complex problems in the future. And an important part of this base is the square.






