What is the rolling friction force and what formula can be used to calculate it?

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

The current state of technology would look completely different if humanity in the distant past had not learned to use the force of rolling friction for its own benefit. What it is, why it appears and how it can be calculated, these issues are discussed in the article.

What is rolling friction?

Under it is understood the physical force that appears in all cases when one object does not slide, but rolls on the surface of another. Examples of rolling friction force are driving a wooden cart wheel on a dirt road or driving a car wheel on asph alt, rolling metal ball and needle bearings on a steel axle, moving a paint roller on a wall, and so on.

Unlike the forces of static and sliding friction, which are caused by interactions at the atomic level of rough surfaces of the body and the surface, the cause of rolling friction is the deformation hysteresis.

Let's explain the named fact on the example of a wheel. When it comes into contact withabsolutely any solid surface, then in the contact zone there is its microdeformation in the elastic region. As soon as the wheel turns through a certain angle, this elastic deformation will disappear, and the body will restore its shape. Nevertheless, as a result of wheel rolling, the cycles of compression and shape recovery are repeated, which are accompanied by energy loss and microscopic disturbances in the structure of the surface layers of the wheel. This loss is called hysteresis. When moving, they manifest themselves in the occurrence of a rolling friction force.

Rolling of non-deformable bodies

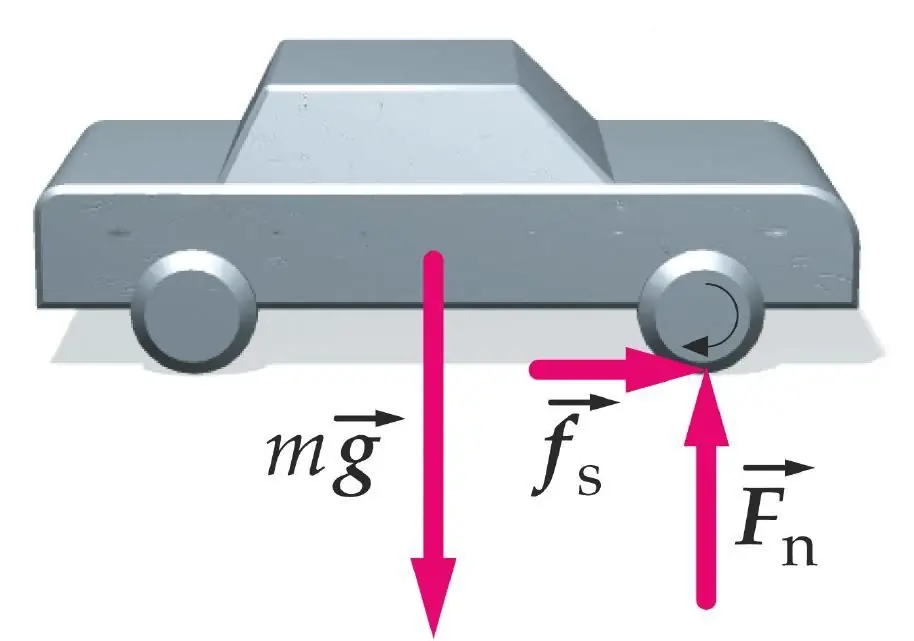
Let's consider the ideal case when the wheel, moving on an absolutely solid surface, does not experience microdeformations. In this case, the zone of its contact with the surface will correspond to a straight segment, the area of which is equal to zero.

When moving, four forces act on the wheel. These are traction force F, support reaction force N, wheel weight P and friction f_r. The first three forces are central in nature (acting on the center of mass of the wheel), so they do not create torque. The force f_{r acts tangentially to the wheel rim. The rolling friction moment is:}

M=f_rr.

Here, the radius of the wheel is indicated by the letter r.

Forces N and P act vertically, therefore, in the case of uniform motion, the friction force f_{rwill be equal to the thrust force F:}

F=f_r.

Any infinitely small force F will be able to overcome f_{r and the wheel will start moving. Thisthe conclusion leads to the fact that in the case of a non-deformable wheel, the rolling friction force is zero.}

Rolling of deformable (real) bodies

In the case of real bodies, as a result of wheel deformation, its area of support on the surface is not equal to zero. As a first approximation, it is a rectangle, with sides l and 2d. Where l is the width of the wheel, which does not interest us much. The appearance of the rolling friction force is due precisely to the value 2d.

As in the case of a non-deformable wheel, the four forces mentioned above also act on a real object. All relationships between them are preserved except for one: the reaction force of the support as a result of deformation will not act through the axle on the wheel, but will be displaced relative to it by a distance d, that is, it will take part in the creation of torque. The formula for the moment M in the case of a real wheel takes the form:

M=Nd - f_rr.

Equality to zero of the value M is the condition for the uniform rolling of the wheel. As a result, we arrive at equality:

f_r=d/rN.

Since N is equal to the weight of the body, we get the final formula for the rolling friction force:

f_r=d/rP.

This expression contains a useful result: as the radius r of the wheel increases, the friction force f_r.

Rolling resistance coefficient and rolling coefficient

Unlike the friction forces of rest and sliding, rolling is characterized by two mutually dependentcoefficients. The first of these is the value of d described above. It is called the rolling resistance coefficient because the larger its value, the greater the force f_{r. For train wheels, automobiles, metal bearings, the value of d lies within tenths of a millimeter.}

The second coefficient is the rolling coefficient itself. It is a dimensionless quantity and is equal to:

C_r=d/r.

In many tables, this value is given, since it is more convenient to use for solving practical problems than the value of d. In most practical cases, the value of C_{r does not exceed a few hundredths (0.01-0.06).}

Rolling condition for real bodies

Above we got the formula for the force f_r. Let's write it through the coefficient C_r:

f_r=C_rP.

It can be seen that its shape is similar to that for the force of static friction, in which instead of C_{r, the value µ is used - the coefficient of static friction.}

Draft force F will cause the wheel to roll only if it is greater than f_r. However, the thrust F can also lead to slip if it exceeds the corresponding rest force. Thus, the condition for the rolling of real bodies is that the force f_{r be less than the static friction force.}

In most cases, the values of the coefficient µ are 1-2 orders of magnitude higher than the value of C_r. However, in some situations (presence of snow, ice,oily liquids, dirt) µ may become smaller than C_{r. In the latter case, wheel slippage will be observed.}