What is a straight prism? Properties and formulas. Task example

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

Stereometry is the study of the characteristics of three-dimensional geometric shapes. One of the well-known volumetric figures that appears in geometry problems is a straight prism. Let's consider in this article what it is, and also describe in detail a prism with a triangular base.

Prism and its types

A prism is a figure that is formed as a result of a parallel translation of a polygon in space. As a result of this geometric operation, a figure is formed, consisting of several parallelograms and two identical polygons parallel to each other. Parallelograms are the sides of the prism, and polygons are its bases.

Any prism has n+2 sides, 3n edges and 2n vertices, where n is the number of corners or sides of the polygonal base. The image shows a pentagonal prism that has 7 sides, 10 vertices and 15 edges.

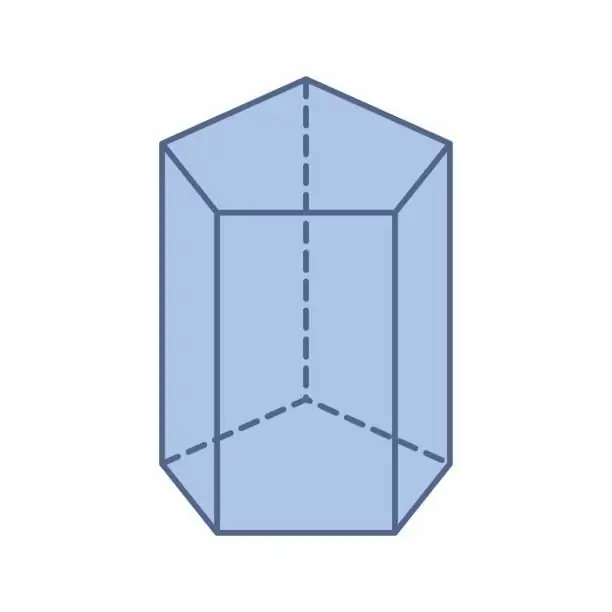
The considered class of figures is represented by several types of prisms. We list them briefly:

• concave and convex;
• oblique and straight;
• wrong and right.

Each figure belongs to one of the listed three types of classification. When solving geometric problems, it is easiest to perform calculations for regular and straight prisms. The latter will be discussed in more detail in the following paragraphs of the article.

What is a straight prism?

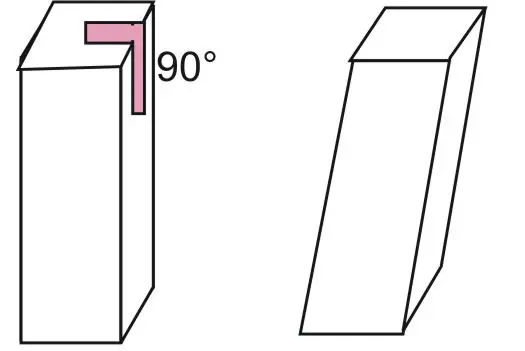
A straight prism is a concave or convex, regular or irregular prism, in which all sides are represented by quadrilaterals with 90° angles. If at least one of the quadrangles of the sides is not a rectangle or square, then the prism is called oblique. Another definition can also be given: a straight prism is such a figure of a given class in which any side edge is equal to the height. Under the height h of the prism, the distance between its bases is assumed.

Both of the given definitions that it is a direct prism are equal and self-sufficient. It follows from them that all dihedral angles between any of the bases and each side are 90°.

It was said above that it is convenient to work with straight figures when solving problems. This is due to the fact that the height matches the length of the side rib. The latter fact facilitates the process of calculating the volume of a figure and the area of its lateral surface.

Volume of a direct prism

Volume - a value inherent in any spatial figure, which numerically reflects the part of the space enclosed between the surfaces of the consideredobject. The volume of a prism can be calculated using the following general formula:

V=S_oh.

That is, the product of the height and the area of the base will give the desired value V. Since the bases of a straight prism are equal, then to determine the area S_oyou can take any of them.

The advantage of using the above formula specifically for a straight prism in comparison with its other types is that it is very easy to find the height of the figure, since it coincides with the length of the side edge.

Side area

It is convenient to calculate not only the volume for a straight figure of the class under consideration, but also its lateral surface. Indeed, any side of it is either a rectangle or a square. Every student knows how to calculate the area of these flat figures, for this it is necessary to multiply adjacent sides by each other.

Assume that the base of the prism is an arbitrary n-gon whose sides are equal to a_i. Index i runs from 1 to n. The area of one rectangle is calculated like this:

S_i=a_ih.

The area of the lateral surface S_bis easy to calculate if you add up all the areas S_i rectangles. In this case, we get the final formula for S_bstraight prism:

S_b=h∑_i=1(a_i)=hP_o.

Thus, to determine the lateral surface area for a straight prism, you must multiply its height by the perimeter of one base.

Problem with a triangular prism

Assume that a straight prism is given. The base is a right triangle. The legs of this triangle are 12 cm and 8 cm. It is necessary to calculate the volume of the figure and its total area if the height of the prism is 15 cm.

First, let's calculate the volume of a straight prism. The triangle (rectangular) located at its bases has an area:

S_o=a₁a₂/2=128/2=48cm².

As you might guess, a₁ and a₂ are legs in this equation. Knowing the base area and height (see the condition of the problem), you can use the formula for V:

V=S_oh=4815=720cm³.

The total area of the figure is formed by two parts: the areas of the bases and the lateral surface. The areas of the two bases are:

S_2o=2S_o=482=96cm².

To calculate the lateral surface area, you need to know the perimeter of a right triangle. Calculate by the Pythagorean theorem its hypotenuse a₃, we have:

a₃ =√(a₁²+ a₂ 2^)=√(122^{+ 8}2^{)=14.42 cm.}

Then the perimeter of the triangle of the base of the right prism will be:

P=a₁+ a₂+ a₃=12 + 8 + 14, 42=34, 42 cm.

Applying the formula for S_b, which was written in the previous paragraph,get:

S_b=hP=1534, 42=516, 3 cm.

Adding the areas of S_2o and S_b, we get the total surface area of the studied geometric figure:

S=S_2o+ S_b=96 + 516, 3=612, 3cm^2.

A triangular prism, which is made from special types of glass, is used in optics to study the spectra of light-emitting objects. Such prisms are able to decompose light into component frequencies due to the phenomenon of dispersion.