Ohm's Law is the basic law of electrical circuits. At the same time, it allows us to explain many natural phenomena. For example, one can understand why electricity does not "beat" the birds that sit on the wires. For physics, Ohm's law is extremely significant. Without his knowledge, it would be impossible to create stable electrical circuits or there would be no electronics at all.
Dependence I=I(U) and its value
The history of the discovery of the resistance of materials is directly related to the current-voltage characteristic. What it is? Let's take a circuit with a constant electric current and consider any of its elements: a lamp, a gas pipe, a metal conductor, an electrolyte flask, etc.
Changing the voltage U (often referred to as V) supplied to the element in question, we will track the change in the strength of the current (I) passing through it. As a result, we will get a dependence of the form I \u003d I (U), which is called the "voltage characteristic of the element" and is a direct indicator of itselectrical properties.
V/A characteristic may look different for different elements. Its simplest form is obtained by considering a metal conductor, which was done by Georg Ohm (1789 - 1854).
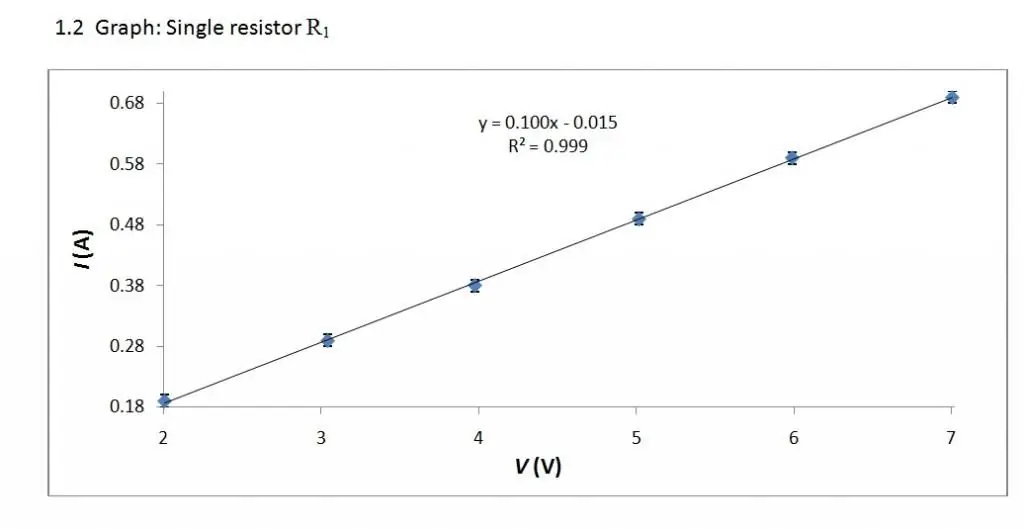
Volt-ampere characteristic is a linear relationship. Therefore, its graph is a straight line.
The law in its simplest form
Ohm's research on the current-voltage characteristics of conductors showed that the current strength inside a metal conductor is proportional to the potential difference at its ends (I ~ U) and inversely proportional to a certain coefficient, that is, I ~ 1/R. This coefficient became known as "conductor resistance", and the unit of measurement of electrical resistance was Ohm or V/A.
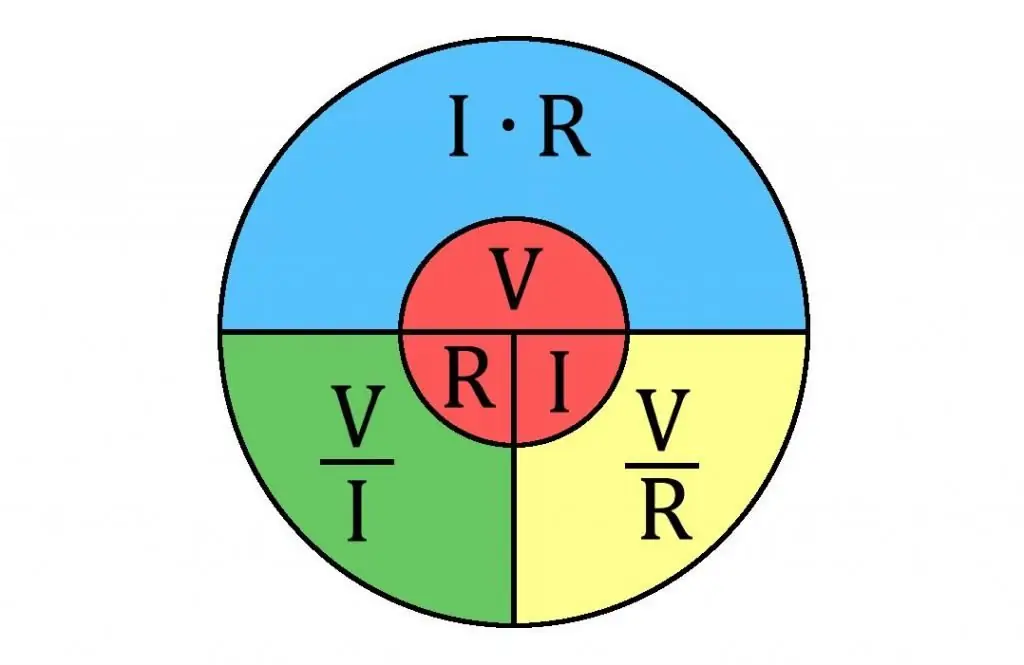
One more thing to note. Ohm's law is often used to calculate resistance in circuits.
Law wording
Ohm's Law says that the current strength (I) of a single section of the circuit is proportional to the voltage in this section and inversely proportional to its resistance.
It should be noted that in this form the law remains true only for a homogeneous section of the chain. Homogeneous is that part of the electrical circuit that does not contain a current source. How to use Ohm's law in an inhomogeneous circuit will be discussed below.
Later, it was experimentally established that the law remains valid for solutionselectrolytes in an electrical circuit.
Physical meaning of resistance
Resistance is a property of materials, substances or media to prevent the passage of electric current. Quantitatively, a resistance of 1 ohm means that in a conductor with a voltage of 1 V at its ends, an electric current of 1 A can pass.
Electrical resistivity
Experimentally, it was found that the resistance of the electric current of the conductor depends on its dimensions: length, width, height. And also on its shape (sphere, cylinder) and the material from which it is made. Thus, the formula for resistivity, for example, of a homogeneous cylindrical conductor will be: R \u003d pl / S.
If in this formula we put s=1 m2 and l=1 m, then R will be numerically equal to p. From here, the unit of measure for the coefficient of resistivity of the conductor in SI is calculated - this is Ohmm.

In the resistivity formula, p is the resistance coefficient determined by the chemical properties of the material from which the conductor is made.
To consider the differential form of Ohm's law, we need to consider a few more concepts.
Current density
As you know, electric current is a strictly ordered movement of any charged particles. For example, in metals, current carriers are electrons, and in conducting gases, ions.
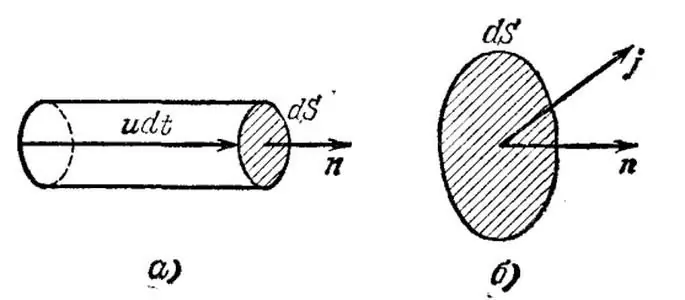
Take the trivial case when all current carriershomogeneous - metal conductor. Let us mentally single out an infinitely small volume in this conductor and denote by u the average (drift, ordered) velocity of electrons in the given volume. Further, let n denote the concentration of current carriers per unit volume.
Now let's draw an infinitesimal area dS perpendicular to the vector u and construct along the velocity an infinitesimal cylinder with a height udt, where dt denotes the time during which all current velocity carriers contained in the considered volume will pass through the area dS.
In this case, the charge equal to q=neudSdt will be transferred by electrons through the area, where e is the electron charge. Thus, the electric current density is a vector j=neu, denoting the amount of charge transferred per unit time through a unit area.
One of the benefits of Ohm's Law differential definition is that you can often get by without calculating the resistance.
Electric charge. Electric field strength
Field strength along with electric charge is a fundamental parameter in the theory of electricity. At the same time, a quantitative idea of them can be obtained from simple experiments available to schoolchildren.
For simplicity, we will consider an electrostatic field. This is an electric field that does not change with time. Such a field can be created by stationary electric charges.
Also, a test charge is needed for our purposes. In its capacity we will use a charged body - so small that it is not capable of causingany perturbations (redistribution of charges) in the surrounding objects.
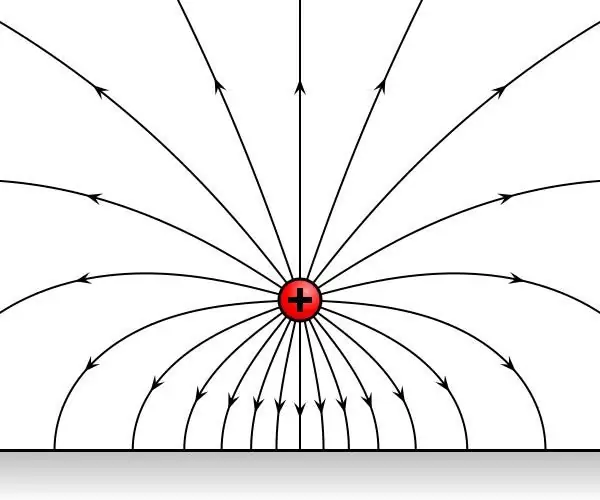
Let's consider in turn two test charges taken, successively placed at one point in space, which is under the influence of an electrostatic field. It turns out that the charges will be subjected to time-invariant influence on his part. Let F1 and F2 be the forces acting on the charges.
As a result of the generalization of experimental data, it was found that the forces F1 and F2 are directed either in one or in opposite directions, and their the ratio F1/F2 is independent of the point in space where the test charges were alternately placed. Therefore, the ratio F1/F2 is a characteristic of the charges themselves, and does not depend on the field.
The discovery of this fact made it possible to characterize the electrification of bodies and was later called electric charge. Thus, by definition, we get q1/q2=F1/F2 , where q1 and q2 - the amount of charges placed at one point of the field, and F1 and F2 - forces acting on charges from the side of the field.
From such considerations, the magnitudes of the charges of various particles were experimentally established. By conditionally setting one of the test charges equal to one in the ratio, you can calculate the value of the other charge by measuring the ratio F1/F2.
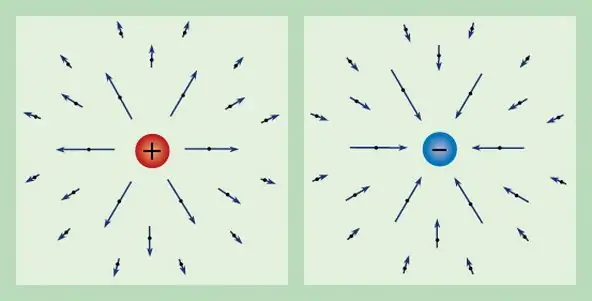
Any electric field can be characterized through a known charge. Thus, the force acting on a unit test charge at rest is called the electric field strength and is denoted by E. From the definition of the charge, we obtain that the strength vector has the following form: E=F/q.
Connection of vectors j and E. Another form of Ohm's law
In a homogeneous conductor, the ordered motion of charged particles will occur in the direction of the vector E. This means that the vectors j and E will be co-directed. As in determining the current density, we select an infinitely small cylindrical volume in the conductor. Then a current equal to jdS will pass through the cross section of this cylinder, and the voltage applied to the cylinder will be equal to Edl. The formula for the resistivity of a cylinder is also known.
Then, writing the formula for the current strength in two ways, we get: j=E/p, where the value 1/p is called electrical conductivity and is the inverse of electrical resistivity. It is usually denoted σ (sigma) or λ (lambda). The unit of conductivity is Sm/m, where Sm is Siemens. Unit inverse of Ohm.
Thus, we can answer the question posed above about Ohm's law for an inhomogeneous circuit. In this case, the current carriers will be affected by the force from the electrostatic field, which is characterized by the intensity E1, and other forces acting on them from another current source, which can be designated E 2. Then Ohm's Law applied toinhomogeneous section of the chain will look like: j=λ(E1 + E2).
More about Conductivity and Resistance
The ability of a conductor to conduct an electric current is characterized by its resistivity, which can be found through the resistivity formula, or conductivity, calculated as the reciprocal of conductivity. The value of these parameters is determined both by the chemical properties of the conductor material and by external conditions. In particular, the ambient temperature.
For most metals, the resistivity at normal temperature is proportional to it, that is, p ~ T. However, deviations are observed at low temperatures. For a large number of metals and alloys at temperatures close to 0°K, the resistance calculation showed zero values. This phenomenon is called superconductivity. For example, mercury, tin, lead, aluminum, etc. have this property. Each metal has its own critical temperature Tk, at which the phenomenon of superconductivity is observed.
Also note that the definition of cylinder resistivity can be generalized to wires made of the same material. In this case, the cross-sectional area from the resistivity formula will be equal to the cross section of the wire, and l - its length.






