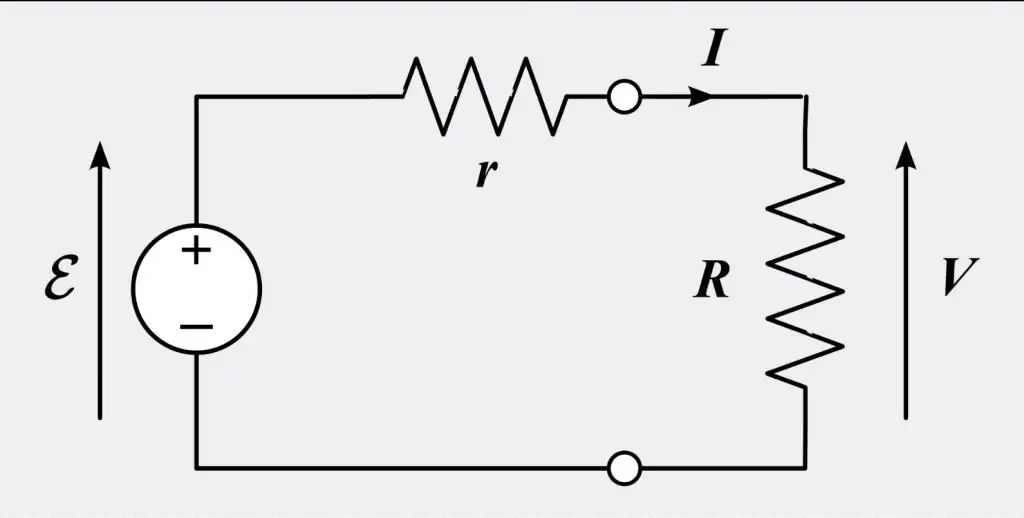
Ohm's Law in differential and integral form states that the current through a conductor between two points is directly proportional to the voltage at the two points. An equation with a constant looks like this:
I=V/R, where I is the point of current through the conductor in units of amperes, V (Volt) is the voltage measured with the conductor in units of volts, R is the resistance of the material being conducted in ohms. More specifically, Ohm's law states that R is a constant in this respect, independent of current.
What can be understood by "Ohm's Law"?
Ohm's Law in differential and integral form is an empirical relationship that accurately describes the conductivity of the vast majority of conductive materials. However, some materials do not obey Ohm's law, they are called "nonohmic". The law was named after the scientist Georg Ohm, who published it in 1827. It describes voltage and current measurements using simple electrical circuits containingvarious wire lengths. Ohm explained his experimental results with a slightly more complex equation than the modern form above.
The concept of Ohm's law in diff. form is also used to denote various generalizations, for example, its vector form is used in electromagnetism and materials science:
J=σE, where J is the number of electrical particles at a particular location in the resistive material, e is the electric field at that location, and σ (sigma) is the material dependent on the conductivity parameter. Gustav Kirchhoff formulated the law exactly like this.
History

History
In January 1781, Henry Cavendish experimented with a Leyden jar and a glass tube of various diameters filled with a s alt solution. Cavendish wrote that speed changes directly as the degree of electrification. Initially, the results were unknown to the scientific community. But Maxwell published them in 1879.
Ohm did his work on resistance in 1825 and 1826 and published his results in 1827 in "The Galvanic Circuit Proved Mathematically". He was inspired by the work of the French mathematician Fourier, who described heat conduction. For experiments, he initially used galvanic piles, but later switched to thermocouples, which could provide a more stable voltage source. He operated with the concepts of internal resistance and constant voltage.
Also in these experiments, a galvanometer was used to measure the current, since the voltagebetween thermocouple terminals proportional to the connection temperature. He then added test leads of various lengths, diameters, and materials to complete the circuit. He found that his data could be modeled with the following equation
x=a /b + l, where x is the meter reading, l is the length of the test lead, a is dependent on the temperature of the thermocouple junction, b is a constant (constant) of the whole equation. Ohm proved his law based on these proportionality calculations and published his results.
Importance of Ohm's Law
Ohm's law in differential and integral form was probably the most important of the early descriptions of the physics of electricity. Today we consider this almost obvious, but when Om first published his work, this was not the case. Critics reacted to his interpretation with hostility. They called his work "naked fantasies" and the German education minister declared that "a professor who preaches such heresy is unworthy of teaching science."
The prevailing scientific philosophy in Germany at the time held that experiments were not necessary to develop an understanding of nature. In addition, Geogr's brother, Martin, a mathematician by profession, struggled with the German educational system. These factors prevented the acceptance of Ohm's work, and his work did not become widely accepted until the 1840s. Nevertheless, Om received recognition for his contributions to science long before his death.
Ohm's law in differential and integral form is an empirical law,generalization of the results of many experiments, which showed that the current is approximately proportional to the electric field voltage for most materials. It is less fundamental than Maxwell's equations and is not suitable in all situations. Any material will break down under the force of a sufficient electric field.
Ohm's Law has been observed on a wide range of scales. At the beginning of the 20th century, Ohm's law was not considered on an atomic scale, but experiments confirm the opposite.
Quantum Beginning
The dependence of the current density on the applied electric field has a fundamentally quantum-mechanical character (classical quantum permeability). A qualitative description of Ohm's law can be based on classical mechanics using the Drude model developed by the German physicist Paul Drude in 1900. Because of this, Ohm's law has many forms, such as the so-called Ohm's law in differential form.
Other forms of Ohm's law
Ohm's law in differential form is an extremely important concept in electrical/electronics engineering because it describes both voltage and resistance. All this is interconnected at the macroscopic level. When studying electrical properties at the macro- or microscopic level, a more related equation is used, which can be called "Ohm's equation", having variables that are closely related to the scalar variables V, I, and R of Ohm's law, but which are a constant function of position inexplorer.
Effect of magnetism

If an external magnetic field (B) is present and the conductor is not at rest, but moving at a speed V, then an additional variable must be added to account for the current induced by the Lorentz force on the charge carriers. Also called Ohm's law of integral form:
J=σ (E + vB).
In the rest frame of a moving conductor, this term is dropped because V=0. There is no resistance because the electric field in the rest frame is different from the E-field in the laboratory frame: E'=E + v × B. Electric and magnetic fields are relative. If J (current) is variable because the applied voltage or E-field varies with time, then reactance must be added to the resistance to account for self-induction. The reactance can be strong if the frequency is high or the conductor is wound.






