Geometry is an extremely interesting science that is taught in Russian schools in the seventh grade. But sometimes the topic covered in the lesson is not at all clear, and attempts to read a paragraph in the textbook only aggravate the situation. Then the omniscient Internet comes to the rescue, or some students simply open ready-made homework assignments, which is fundamentally wrong, because then the question remains unanswered, the brain does not develop, there are even more problems with the perception of information in the lesson, which leads to poor grades. In this article, we will analyze one of the basic elements, with the help of which many tasks are solved. What is the definition of the height of a triangle? How to build it? You will find answers to these and many other questions in this article.
Determining the height of a triangle
Understanding the essence of the element, and why it is needed, always begins with the study of theory. Thus, the height of a triangle is a perpendicular dropped from the vertex of the triangle to the line containing the opposite side. Why not on the side? We will deal with this a little later.

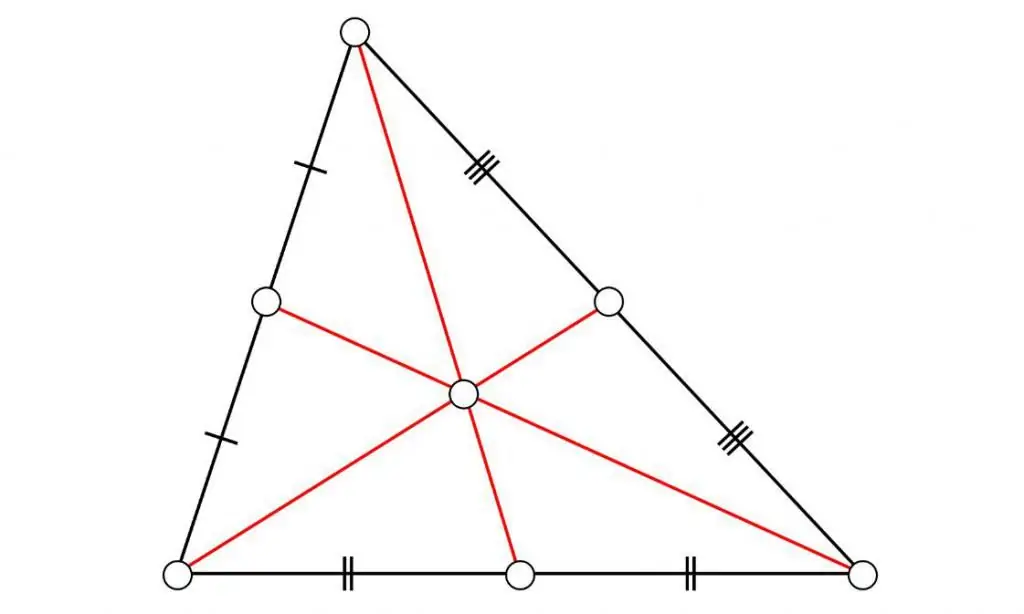
As much as possibledraw heights in a triangle? The number of heights is the same as the number of vertices, that is, three. All three intersections of the triangle's perpendiculars intersect at one point.
Let's also repeat the theory about two other important elements - the bisector and the median.
Bisector - a ray connecting the vertex of a triangle with the opposite side, while dividing the angle into two equal parts.
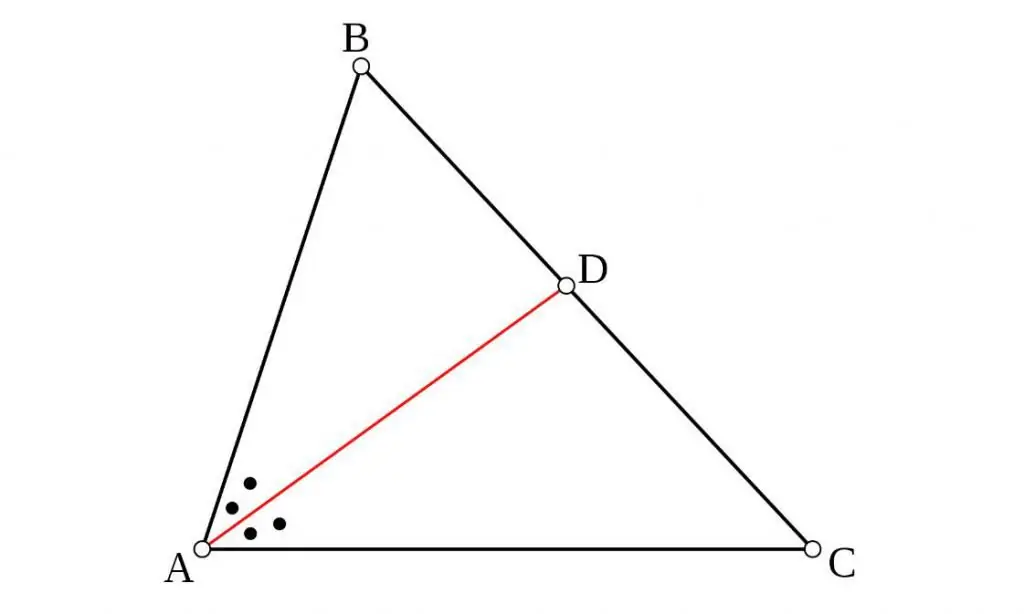
Median is a segment connecting the vertex of an angle with the midpoint of the opposite side.
Types of Triangles
There are a lot of varieties of triangles in geometry, in each of them the heights play their role. Let's look at all the types of this figure in detail. Determining the height of the triangle will help us with this.
Let's start with an ordinary acute-angled scalene triangle, in which all angles are acute and not equal to 60 degrees, and the sides are not equal to each other. In this geometric figure, the heights will intersect, but this point will not be the center of the triangle.
In an obtuse triangle, the measure of one angle is greater than 90 degrees. The height coming out of an obtuse angle is lowered to a straight line containing the opposite side.
The next is an isosceles triangle. It has only two sides and two angles at the base. Interestingly, the height drawn from the vertex to the base of the triangle coincides with the median and bisector.
In an equilateral triangle, all sides and angles that are equal to 60 degrees (each) are equal. All heights, medians andthe bisectors coincide and intersect at one point - the center of the triangle.

Standard height-related formulas
For each of the above cases, there are formulas for determining the height, but in this paragraph we will consider only those that are suitable for each type of triangle. There are four such formulas.
- The simplest and most affordable: H=2S/a. Knowing the area and the length of the side to which the perpendicular is drawn, we can find the height by dividing the double product of the area by the side.
- If the triangle is enclosed in a circle, then there is a formula for this case: H=bc/2R. To find the height, you need to divide the sides on which the perpendicular does not fall by the double product of the radius of the circle circumscribed around the triangle.
- Knowing only the sides, we can also find the height: H=(2√(p(p-a)(p-b)(p-c)))/a, where: p is the half-perimeter; a - the side on which the height is lowered; b, c - sides on which the perpendicular does not fall.
- And for those who know have already started to pass trigonometry and know what sine and cosine are, there is such a formula: H=bsinY=csinB. Sine - the ratio of the opposite side to the perpendicular; H - perpendicular; b and c are the sides opposite the angles Y and B, respectively.
Right triangle
You might think that we forgot about right triangles, but we didn't. A right triangle is a triangle in which one of the angles is 90 degrees. There is only one height in a right triangle, because the other two aresides, or rather the legs. The only perpendicular leaves the right angle and descends to the hypotenuse. There are a lot of formulas for finding for this case:
- H=ab/c;
- H=ab/√(a2 +b 2);
- H=csinAcosA=c sinBcosB;
- H=bsinA=a sinB;
- H=√de.
where:
H - height;
a, b - legs;
c - hypotenuse;
A, B - angles at the hypotenuse;
d, e - segments obtained by dividing the hypotenuse by height.
Conclusion
So, in this article we have considered the definition of the height of a triangle. What are the types of triangles? What formulas can be used to find height? Now you can give detailed, and most importantly, correct answers to all these questions.






