Propositional algebra is an exact science that does not compromise. To solve examples with conjunction, disjunction, implication, and so on, you can build a truth table in the Excel application. It is equipped with a set of logical functions that automate and facilitate the process of finding the result.
Mathematical logic: basic concepts
Aristotle is considered the founder of formal logic. In the 17th century G. Leibniz suggested introducing symbols to define statements. D. Buhl consolidated the acquired knowledge and for the first time marked sentences with symbols.
Schematically, "TRUE" is replaced by 1, and "FALSE" by 0.
Under the statement is understood any declarative sentence that gives any information and is capable of taking the value of truth or falsity. In algebra, logics are abstracted from the semantic load of sentences and consider only logical values.
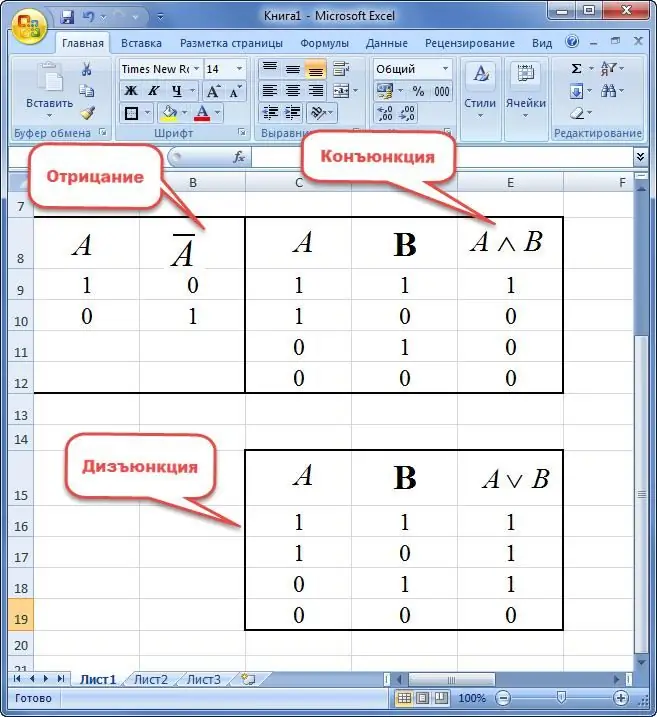
Negative is a new expression that takes the value of true if it is false and vice versa.
Conjunction of twovariables is called a new sentence, which takes the value of truth in the case of simultaneous designation "1" and falsity in other situations.
The disjunction of two statements is understood as a new expression that takes the value "FALSE" only if there are "0" and "TRUE" in other variations at the same time.
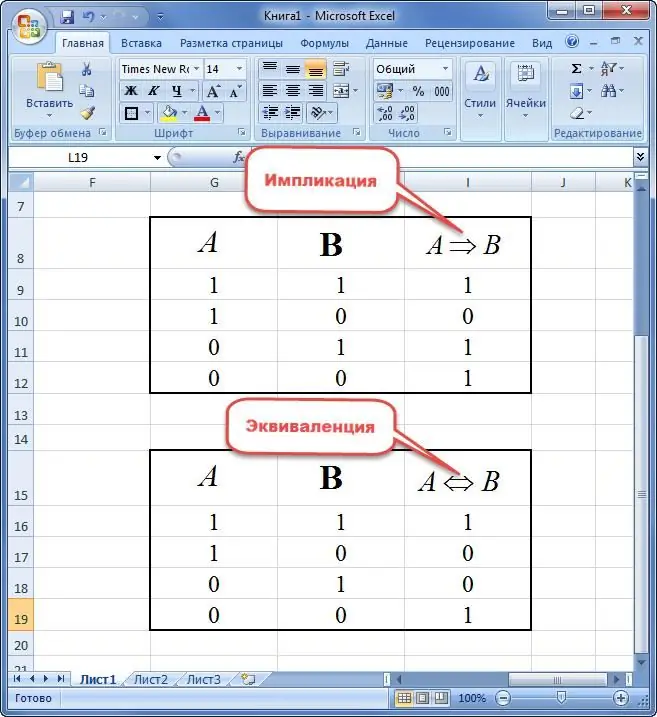
An implication of two variables is a new sentence in which:
- if the premise is true and the consequence is false, then the expression equals "0";
- statement equals "1" in other cases.
Equivalent of two variables is understood as a new statement that takes the value of truth only if the elements are the same. Otherwise, the offer is "0".
Logical values of expressions are usually presented in tabular form. There is another name for this kind of information. They say that for a statement you need to build a truth table. It specifies the initial values for all variables, and then the result of the entire expression is calculated.
Algorithm for implementing calculations in logical operations
To build a truth table, you need to know the order in which the actions are performed. In an expression with multiple operands, the calculation is performed in the following order:
- inversion (negation);
- conjunction (logical function in Excel "AND");
- disjunction (boolean operator in Excel "OR");
- implication (consequence);
- equivalence.
There are two more operations, but their priority is not defined:
- Schaeffer's stroke;
- Pierce arrow.
The calculation algorithm changes if the expression is enclosed in brackets.
The order of constructing a tabular form for logical operands in Excel
Before finding the value of an expression, you need to study the concept of a logic algebra formula. The definition says that this is a complex expression, consisting of the simplest statements connected by logical operands.
Example 1. Construct a truth table for conjunction, disjunction and negation.
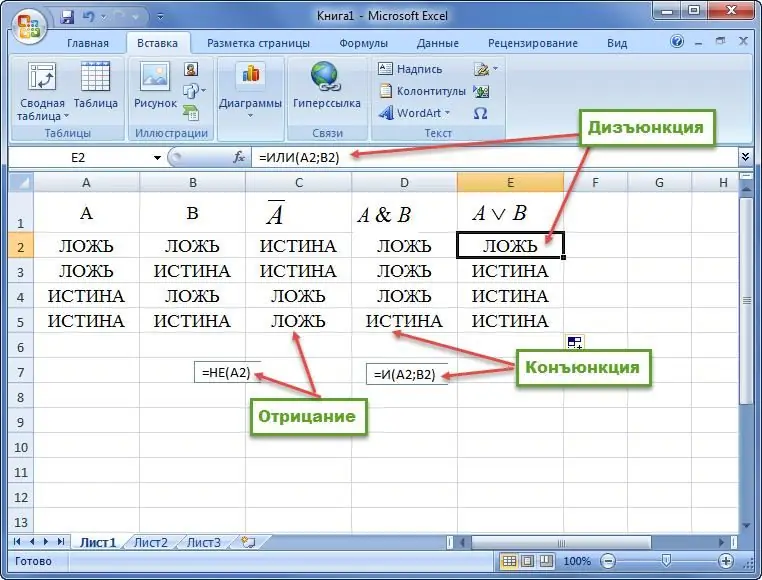
Example 2. Given a formula for the algebra of logic. Build a truth table. Sample examples are given below.
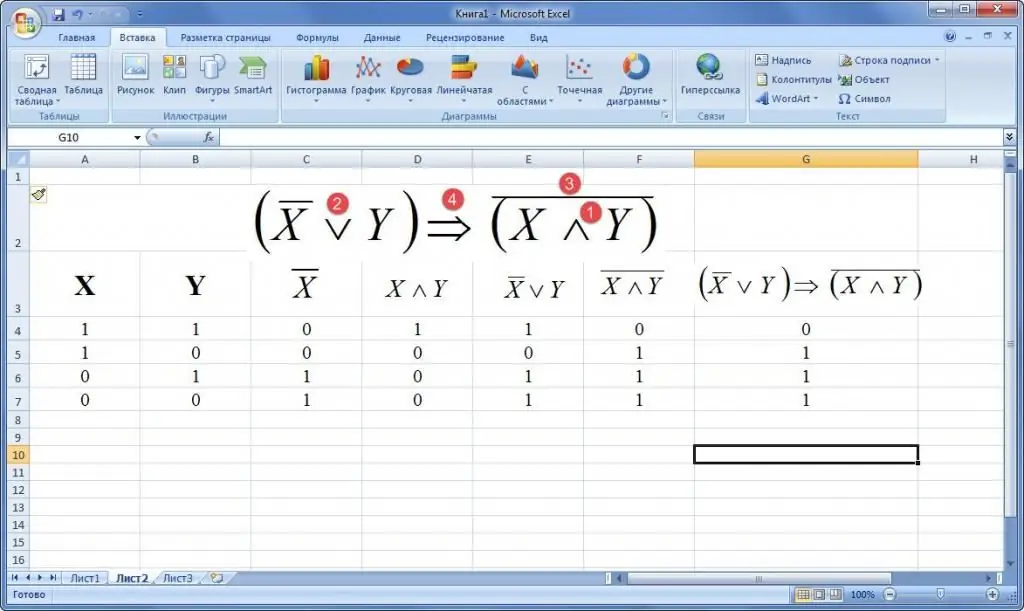
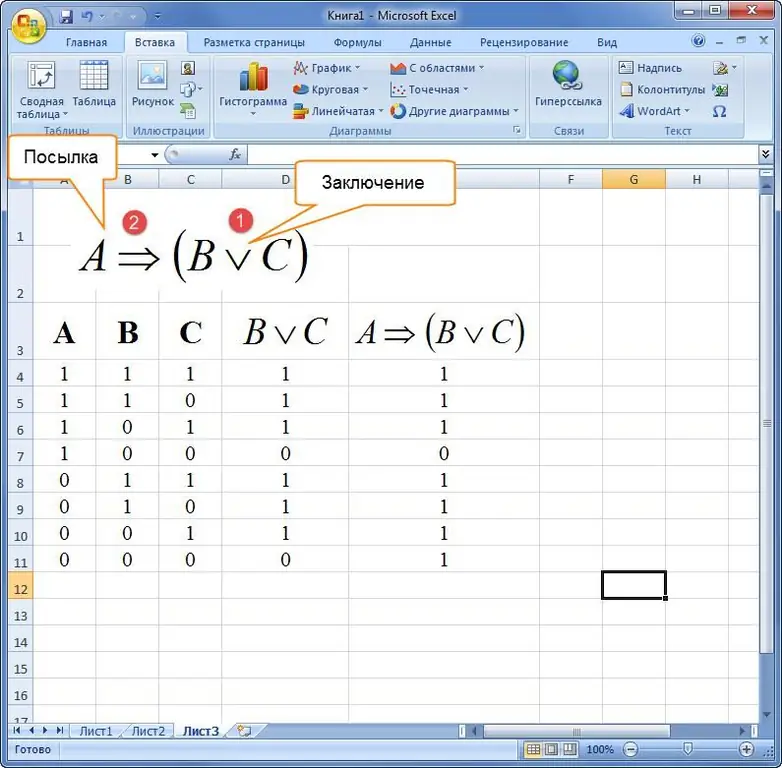
Example 3. How to build a truth table in Excel, given a formula of logic algebra in a verbal description. Statement: "If a triangle is equilateral, then all its edges are equal or all its angles are equal."
First, you need to parse the compound sentence into minimal elements:
- The first part of the expression: A="equilateral triangle".
- Second: B="all sides of the figure are equal".
- Third: C="all angles of a triangle are equal".
After that, an expression is compiled and solved in the Excel software package.
When compiling truth tables, it is important to remember the order of operations.






