The law of conservation of momentum and angular momentum: an example of solving the problem

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

When you have to solve problems in physics on the movement of objects, it often turns out to be useful to apply the law of conservation of momentum. What is the momentum for the linear and circular movement of the body, and what is the essence of the law of conservation of this value, is discussed in the article.

The concept of linear momentum

Historical data show that for the first time this value was considered in his scientific works by Galileo Galilei at the beginning of the 17th century. Subsequently, Isaac Newton was able to harmoniously integrate the concept of momentum (a more correct name for momentum) into the classical theory of the movement of objects in space.

Denote the momentum as p¯, then the formula for its calculation will be written as:

p¯=mv¯.

Here m is the mass, v¯ is the speed (vector value) of the movement. This equality shows that the amount of motion is the velocity characteristic of an object, where the mass plays the role of a multiplication factor. Number of movementis a vector quantity pointing in the same direction as the velocity.

It is intuitively clear that the greater the speed of movement and the mass of the body, the more difficult it is to stop it, that is, the greater the kinetic energy it has.

The amount of movement and its change

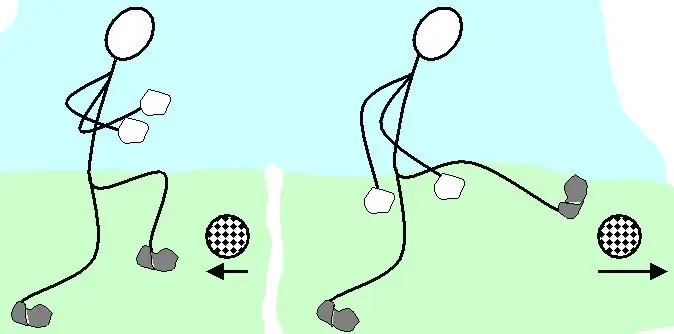
You can guess that to change the p¯ value of the body, you need to apply some force. Let the force F¯ act during the time interval Δt, then Newton's law allows us to write the equality:

F¯Δt=ma¯Δt; therefore F¯Δt=mΔv¯=Δp¯.

The value equal to the product of the time interval Δt and the force F¯ is called the impulse of this force. Since it turns out to be equal to the change in momentum, the latter is often called simply momentum, suggesting that some external force F¯ created it.

Thus, the reason for the change in the momentum is the momentum of the external force. The value of Δp¯ can lead both to an increase in the value of p¯ if the angle between F¯ and p¯ is acute, and to a decrease in the modulus of p¯ if this angle is obtuse. The simplest cases are the acceleration of the body (the angle between F¯ and p¯ is zero) and its deceleration (the angle between the vectors F¯ and p¯ is 180o).

When momentum is conserved: law

If the body system is notexternal forces act, and all processes in it are limited only by the mechanical interaction of its components, then each component of the momentum remains unchanged for an arbitrarily long time. This is the law of conservation of momentum of bodies, which is mathematically written as follows:

p¯=∑_ip_{i¯=const or}

∑_ip_ix=const; ∑_ip_iy=const; ∑_ip_iz=const.

The subscript i is an integer that enumerates the object of the system, and the indices x, y, z describe the momentum components for each of the coordinate axes in the Cartesian rectangular system.

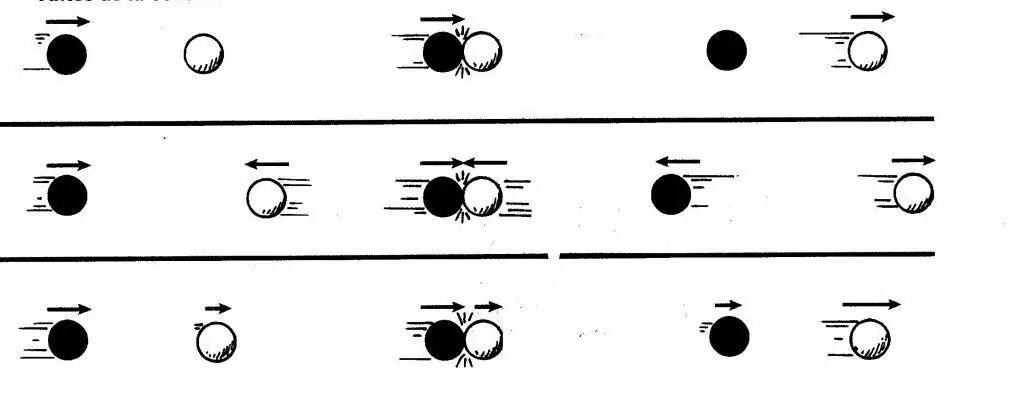
In practice, it is often necessary to solve one-dimensional problems for the collision of bodies, when the initial conditions are known, and it is necessary to determine the state of the system after the impact. In this case, momentum is always conserved, which cannot be said about kinetic energy. The latter before and after the impact will be unchanged only in a single case: when there is an absolutely elastic interaction. For this case of collision of two bodies moving with velocities v₁ and v_{2, the momentum conservation formula will take the form:}

m₁ v₁ + m₂ v ₂=m₁ u₁ + m₂ u 2_.

Here, the velocities u₁ and u_{2 characterize the movement of bodies after the impact. Note that in this form of the conservation law, it is necessary to take into account the sign of the velocities: if they are directed towards each other, then one should be takenpositive and the other negative.}

For a perfectly inelastic collision (two bodies stick together after impact), the law of conservation of momentum has the form:

m₁ v₁ + m₂ v ₂=(m₁+ m_2)u.

Solution of the problem on the law of conservation of p¯

Let's solve the following problem: two balls roll towards each other. The masses of the balls are the same, and their speeds are 5 m/s and 3 m/s. Assuming that there is an absolutely elastic collision, it is necessary to find the speeds of the balls after it.

Using the law of conservation of momentum for the one-dimensional case, and also taking into account that the kinetic energy is conserved after the impact, we write:

v_{1 -} v₂=u₁ + u _2;

v₁² + v₂^2=u12 ^{+ u}22^.

Here we immediately reduced the masses of the balls due to their equality, and also took into account the fact that the bodies move towards each other.

It is easier to continue solving the system if you substitute known data. We get:

5 - 3 - u₂=u_1;

5²+ 3²=u₁²+ u₂^2.

Substituting u_{1 into the second equation, we get:}

2 - u₂=u_1;

34=(2 - u₂)²+u₂ 2^{=4 - 4u}2 _{+ 2u}22^{; hence,u}22^{- 2u}2 _{- 15=0.}

We got the classic quadratic equation. We solve it through the discriminant, we get:

D=4 - 4(-15)=64.

u_{2=(2 ± 8) / 2=(5; -3) m/c.}

We got two solutions. If we substitute them into the first expression and define u₁, then we get the following value: u₁=-3 m/s, u ₂=5 m/s; u₁=5 m/s, u_{2=-3 m/s. The second pair of numbers is given in the condition of the problem, so it does not correspond to the real distribution of velocities after the impact.}

Thus, only one solution remains: u₁=-3 m/s, u_{2=5 m/s. This curious result means that in a central elastic collision, two balls of equal mass simply exchange their velocities.}

Moment of momentum

Everything that was said above refers to the linear type of movement. However, it turns out that similar quantities can also be introduced in the case of circular displacement of bodies around a certain axis. The angular momentum, which is also called angular momentum, is calculated as the product of the vector connecting the material point with the axis of rotation and the momentum of this point. That is, the formula takes place:

L¯=r¯p¯, where p¯=mv¯.

Momentum, like p¯, is a vector that is directed perpendicular to the plane built on the vectors r¯ and p¯.

The value of L¯ is an important characteristic of a rotating system, since it determines the energy that is stored in it.

Moment of momentum and conservation law

The angular momentum is conserved if no external forces act on the system (usually they say that there is no moment of forces). The expression in the previous paragraph, through simple transformations, can be written in a form more convenient for practice:

L¯=Iω¯, where I=mr2 is the moment of inertia of the material point, ω¯ is the angular velocity.

The moment of inertia I, which appeared in the expression, has exactly the same meaning for rotation as the usual mass for linear motion.

If there is any internal rearrangement of the system, in which I changes, then ω¯ also does not remain constant. Moreover, the change in both physical quantities occurs in such a way that the equality below remains valid:

I₁ ω₁¯=I₂ ω _2¯.

This is the law of conservation of angular momentum L¯. Its manifestation was observed by every person who at least once attended ballet or figure skating, where athletes perform pirouettes with rotation.