Lateral surface of a regular and truncated cone. Formulas and an example of solving the problem

2024 Author: Angel Austin | [email protected]. Last modified: 2023-12-17 05:14

When considering figures in space, problems often arise in determining their surface area. One such figure is the cone. Consider in the article what is the side surface of a cone with a round base, as well as a truncated cone.

Cone with round base

Before proceeding to consider the lateral surface of the cone, let's show what kind of figure it is and how to get it using geometric methods.

Take a right-angled triangle ABC, where AB and AC are legs. Let's put this triangle on leg AC and rotate it around leg AB. As a result, sides AC and BC describe two surfaces of the figure shown below.

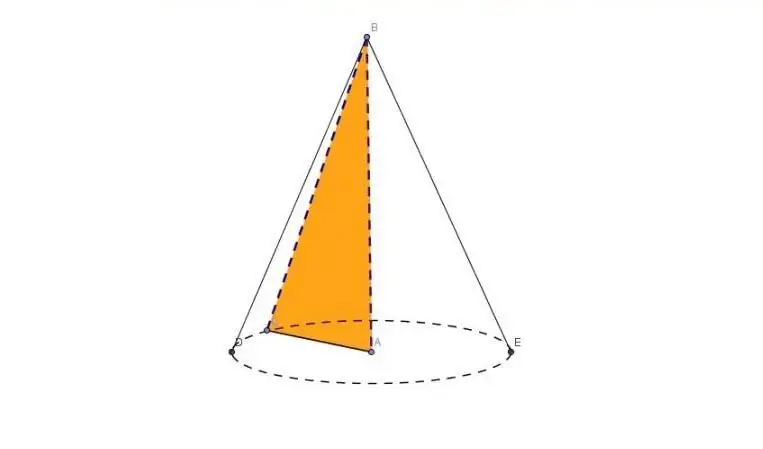
The figure obtained by rotation is called a round straight cone. It is round because its base is a circle, and straight because a perpendicular drawn from the top of the figure (point B) intersects the circle at its center. The length of this perpendicular is called the height. Obviously, it is equal to leg AB. The height is usually denoted by the letter h.

Besides the height, the considered cone is described by two more linear characteristics:

• generating, or generatrix (hypotenuse BC);
• base radius (leg AC).

The radius will be denoted by the letter r, and the generatoratrix by g. Then, taking into account the Pythagorean theorem, we can write an equality important for the figure under consideration:

g²=h²+ r²

Conical surface

The totality of all generatrices forms a conical or lateral surface of a cone. In appearance, it is difficult to tell which flat figure it corresponds to. The latter is important to know when determining the area of a conical surface. To solve this problem, the sweep method is used. It consists in the following: a surface is mentally cut along an arbitrary generatrix, and then it is unfolded on a plane. With this method of obtaining a sweep, the following flat figure is formed.

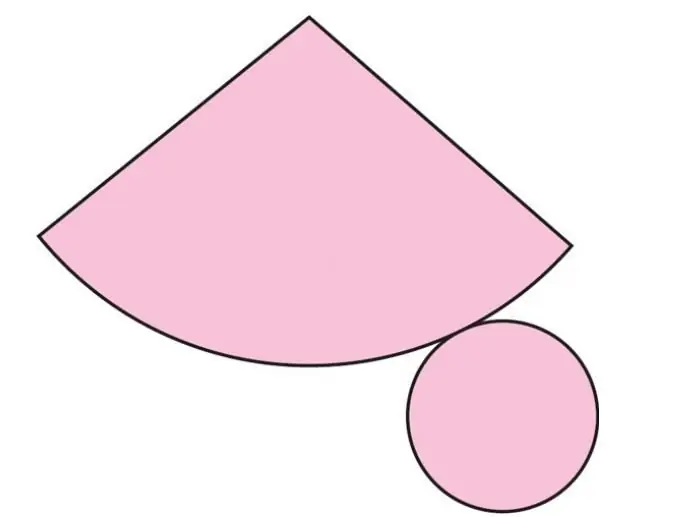
As you might guess, the circle corresponds to the base, but the circular sector is a conical surface, the area of which we are interested in. The sector is bounded by two generatrices and an arc. The length of the latter is exactly equal to the perimeter (length) of the circumference of the base. These characteristics uniquely determine all properties of the circular sector. We will not give intermediate mathematical calculations, but immediately write down the final formula, using which you can calculate the area of the lateral surface of the cone. The formula is:

S_b=pigr

The area of a conical surface S_bis equal to the product of two parameters and Pi.

Truncated cone and its surface

If we take an ordinary cone and cut off its top with a parallel plane, the remaining figure will be a truncated cone. Its lateral surface is limited by two round bases. Let's denote their radii as R and r. We denote the height of the figure by h, and the generatrix by g. Below is a paper cutout for this figure.

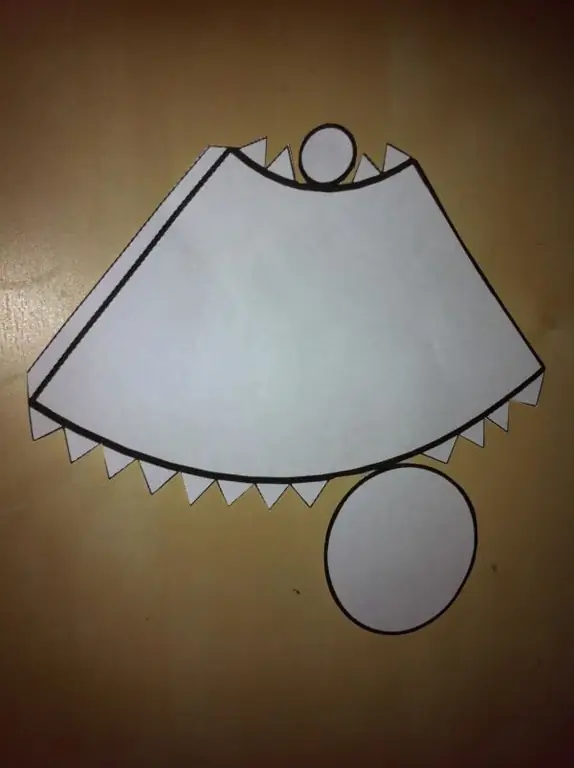
It can be seen that the side surface is no longer a circular sector, it is smaller in area, since the central part was cut off from it. The development is limited to four lines, two of them are straight line segments-generators, the other two are arcs with the lengths of the corresponding circles of the bases of the truncated cone.

Side surface S_bcalculated as follows:

S_b=pig(r + R)

Generatrix, radii and height are related by the following equality:

g²=h²+ (R - r)²

The problem with the equality of the areas of figures

Given a cone with a height of 20 cm and a base radius of 8 cm. It is necessary to find the height of a truncated cone whose lateral surface will have the same area as this cone. The truncated figure is built on the same base, and the radius of the upper base is 3 cm.

First of all, let's write down the condition of equality of the areas of the cone and the truncated figure. We have:

S_b1=S_b2=>

pig₁R=pig₂(r + R)

Now let's write the expressions for the generatrices of each shape:

g₁=√(R²+ h₁²);

g₂=√((R-r)² + h₂ ²)

Substitute g₁ and g₂ into the formula for equal areas and square the left and right sides, we get:

R²(R²+ h₁²)=((R-r)²+ h₂²)(r + R)²

Where we get the expression for h₂:

h₂=√(R²(R²+ h 12^{)/(r + R)}2^{- (R - r)}2 ⁾

We will not simplify this equality, but simply substitute the data known from the condition:

h₂=√(8²(8²+ 202^{)/(3 + 8)}2^{- (8 - 3)}2^{) ≈ 14.85 cm}

Thus, in order to equal the areas of the side surfaces of the figures, the truncated cone must have the parameters: R=8 cm, r=3 cm, h₂ ≈ 14, 85 cm.