An important geometric object that is studied in flat space is a straight line. In three-dimensional space, in addition to the straight line, there is also a plane. Both objects are conveniently defined using direction vectors. What is it, how are these vectors used to determine the equations of a straight line and a plane? These and other questions are covered in the article.
Direct line and how to define it

Each student has a good idea of what geometric object they are talking about. From the point of view of mathematics, a straight line is a set of points, which, in the case of their arbitrary pairwise connection, lead to a set of parallel vectors. This definition of a line is used to write an equation for it in both two and three dimensions.
To describe the considered one-dimensional object, different types of equations are used, which are listed in the list below:
- general view;
- parametric;
- vector;
- canonical or symmetrical;
- in segments.
Each of these species has some advantages over the others. For example, an equation in segments is convenient to use when studying the behavior of a straight line relative to the coordinate axes, a general equation is convenient when finding a direction perpendicular to a given straight line, as well as when calculating the angle of its intersection with the x-axis (for a flat case).
Since the topic of this article is related to the directing vector of a straight line, we will further consider only the equation where this vector is fundamental and is contained explicitly, that is, a vector expression.
Specifying a straight line through a vector
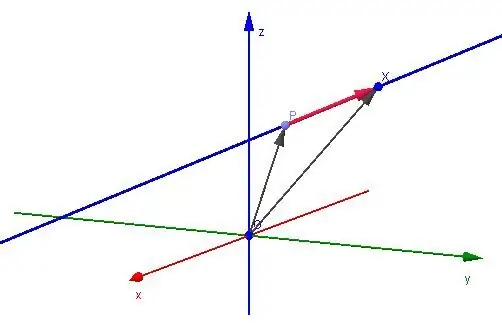
Suppose we have some vector v¯ with known coordinates (a; b; c). Since there are three coordinates, the vector is given in space. How to depict it in a rectangular coordinate system? This is done very simply: on each of the three axes, a segment is plotted, the length of which is equal to the corresponding coordinate of the vector. The intersection point of the three perpendiculars restored to the xy, yz and xz planes will be the end of the vector. Its beginning is the point (0; 0; 0).
Nevertheless, the given position of the vector is not the only one. Similarly, you can draw v¯, placing its origin at an arbitrary point in space. These arguments say that it is impossible to set a specific line using a vector. It defines a family of an infinite number of parallel lines.
Nowfix some point P(x0; y0; z0) of space. And we set the condition: a straight line must pass through P. In this case, the vector v¯ must also contain this point. The last fact means that one single line can be defined using P and v¯. It will be written as the following equation:
Q=P + λ × v¯
Here Q is any point belonging to the line. This point can be obtained by choosing the appropriate parameter λ. The written equation is called the vector equation, and v¯ is called the direction vector of the straight line. By arranging it so that it passes through P and changing its length with the parameter λ, we get each point of Q as a straight line.
In coordinate form, the equation will be written as follows:
(x; y; z)=(x0; y0; z0) + λ × (a; b; c)
And in explicit (parametric) form, you can write:
x=x0+ λ × a;
y=y0+ λ × b;
z=z0+ λ × c
If we exclude the third coordinate in the above expressions, then we get the vector equations of the straight line on the plane.
For what tasks is it useful to know the direction vector ?
As a rule, these are tasks to determine the parallelism and perpendicularity of lines. Also, the direct vector that determines the direction is used when calculating the distance between straight lines and a point and a straight line, to describe the behavior of a straight line relative to a plane.
Twolines will be parallel if their direction vectors are. Accordingly, the perpendicularity of lines is proved using the perpendicularity of their vectors. In these types of problems, it is enough to calculate the scalar product of the considered vectors to get the answer.
In the case of tasks for calculating the distances between lines and points, the direction vector is explicitly included in the corresponding formula. Let's write it down:
d=|[P1P2¯ × v¯] | / |v¯|
Here P1P2¯ - built on points P1 and P 2 directed segment. The point P2 is arbitrary, lying on the line with the vector v¯, while the point P1 is the one to which the distance should be determined. It can be either independent or belong to another line or plane.
Note that it makes sense to calculate the distance between lines only when they are parallel or intersecting. If they intersect, then d is zero.
The above formula for d is also valid for calculating the distance between a plane and a straight line parallel to it, only in this case P1should belong to the plane.
Let's solve several problems to better show how to use the considered vector.
Vector Equation Problem
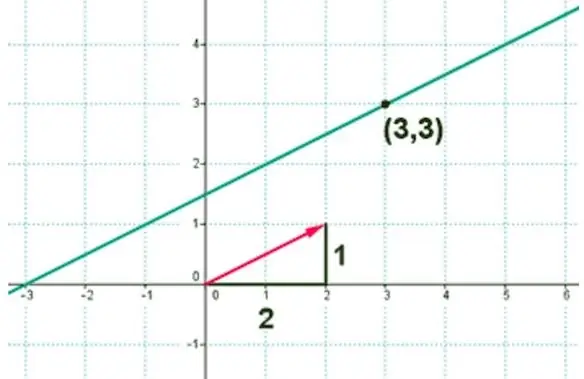
It is known that a straight line is described by the following equation:
y=3 × x - 4
You should write the appropriate expression invector form.
This is a typical equation of a straight line, known to every schoolchild, written in general form. Let's show how to rewrite it in vector form.
The expression can be represented as:
(x; y)=(x; 3 × x - 4)
It can be seen that if you open it, you get the original equality. Now we divide its right side into two vectors so that only one of them contains x, we have:
(x; y)=(x; 3 × x) + (0; -4)
It remains to take x out of brackets, designate it with a Greek symbol and swap the vectors of the right side:
(x; y)=(0; -4) + λ × (1; 3)
We got the vector form of the original expression. Direction vector coordinates of the straight line are (1; 3).
The task of determining the relative position of lines

Two lines are given in space:
(x; y; z)=(1; 0; -2) + λ × (-1; 3; 1);
(x; y; z)=(3; 2; 2) + γ × (1; 2; 0)
Are they parallel, crossing or intersecting?
Non-zero vectors (-1; 3; 1) and (1; 2; 0) will be guides for these lines. Let us express these equations in parametric form and substitute the coordinates of the first into the second. We get:
x=1 - λ;
y=3 × λ;
z=-2 + λ;
x=3 + γ=1 - λ=>γ=-2 - λ;
y=2 + 2 × γ=3 × λ=> γ=3 / 2 × λ - 1;
z=2=-2 + λ=> λ=4
Substitute the found parameter λ into the two equations above, we get:
γ=-2 - λ=-6;
γ=3 / 2 × λ - 1=5
Parameter γ cannot take two different values at the same time. This means that the lines do not have a single common point, that is, they are intersecting. They are not parallel, since non-zero vectors are not parallel to each other (for their parallelism, there must be a number that, by multiplying by one vector, would lead to the coordinates of the second).
Mathematical description of the plane
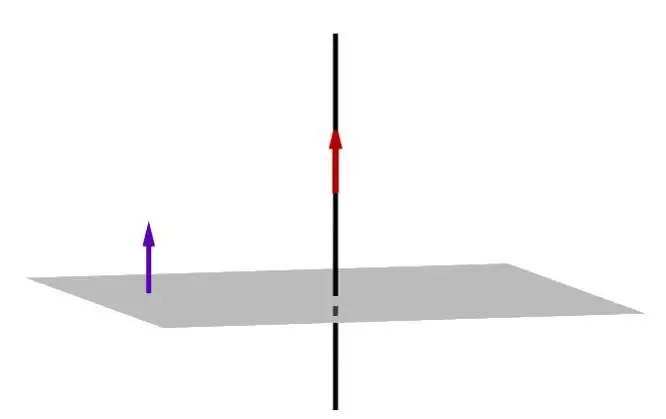
To set a plane in space, we give a general equation:
A × x + B × y + C × z + D=0
Here Latin capital letters represent specific numbers. The first three of them define the coordinates of the normal vector of the plane. If it is denoted by n¯, then:
n¯=(A; B; C)
This vector is perpendicular to the plane, so it is called a guide. Its knowledge, as well as the known coordinates of any point belonging to the plane, uniquely determine the latter.
If the point P(x1; y1; z1) belongs to the plane, then the intercept D is calculated as follows:
D=-1 × (A × x1+ B × y1 + C × z1)
Let's solve a couple of problems using the general equation for the plane.
Task forfinding the normal vector of the plane
The plane is defined as follows:
(y - 3) / 2 + (x + 1) / 3 - z / 4=1
How to find a direction vector for her?
From the above theory it follows that the coordinates of the normal vector n¯ are the coefficients in front of the variables. In this regard, to find n¯, the equation should be written in general form. We have:
1 / 3 × x + 1 / 2 × y - 1 / 4 × z - 13 / 6=0
Then the normal vector of the plane is:
n¯=(1/3; 1/2; -1/4)
The problem of drawing up the equation of the plane

The coordinates of three points are given:
M1(1; 0; 0);
M2(2; -1; 5);
M3(0; -2; -2)
What will the equation of the plane containing all these points look like.
Through three points that do not belong to the same line, only one plane can be drawn. To find its equation, we first calculate the direction vector of the plane n¯. To do this, we proceed as follows: we find arbitrary two vectors belonging to the plane, and calculate their vector product. It will give a vector that will be perpendicular to this plane, that is, n¯. We have:
M1M2¯=(1; -1; 5); M1M3¯=(-1; -2; -2);
n¯=[M1M2¯ × M1M 3¯]=(12; -3; -3)
Take the point M1to drawplane expressions. We get:
D=-1 × (12 × 1 + (-3) × 0 + (-3) × 0)=-12;
12 × x - 3 × y - 3 × z - 12=0=>
4 × x - y - z - 4=0
We have obtained a general type expression for a plane in space by first defining a direction vector for it.
The cross product property should be remembered when solving problems with planes, since it allows you to easily determine the coordinates of a normal vector.






