Often in physics one has to solve problems for calculating equilibrium in complex systems that have many acting forces, levers and axes of rotation. In this case, it is easiest to use the concept of moment of force. This article provides all the necessary formulas with detailed explanations that should be used to solve problems of the named type.
What will we talk about?

Many people probably noticed that if you act with any force on an object fixed at a certain point, it starts to rotate. A striking example is the door to the house or to the room. If you take it by the handle and push (apply force), then it will begin to open (turn on its hinges). This process is a manifestation in everyday life of the action of a physical quantity, which is called the moment of force.
From the described example with the door it follows that the value in question indicates the ability of the force to rotate, which is its physical meaning. Also this valueis called the moment of torsion.
Determining the moment of force
Before defining the quantity under consideration, let's take a simple picture.
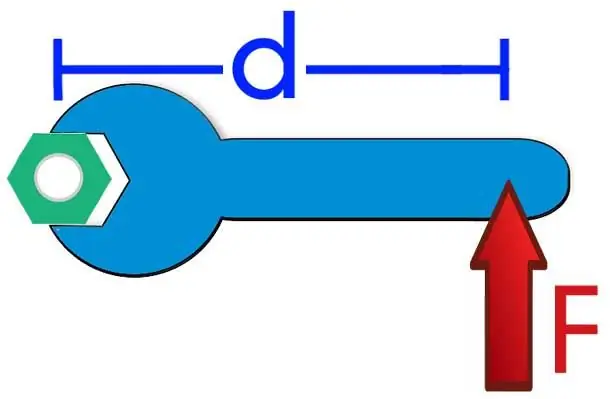
So, the figure shows a lever (blue), which is fixed on the axis (green). This lever has length d, and a force F is applied to its end. What will happen to the system in this case? That's right, the lever will begin to rotate counterclockwise when viewed from above (note that if you stretch your imagination a little and imagine that the view is directed from below to the lever, then it will rotate clockwise).
Let the point of attachment of the axis be called O, and the point of application of force - P. Then, we can write the following mathematical expression:
OP¯ F¯=M¯FO.
Where OP¯ is the vector that is directed from the axis to the end of the lever, it is also called the force lever, F¯ is the vector applied force to point P, and M¯FO is the moment of force about point O (axis). This formula is the mathematical definition of the physical quantity in question.
Direction of moment and right hand rule
The expression above is a cross product. As you know, its result is also a vector that is perpendicular to the plane passing through the corresponding multiplier vectors. This condition is satisfied by two directions of the value M¯FO (down and up).
To uniquelyto determine, one should use the so-called right-hand rule. It can be formulated in this way: if you bend four fingers of your right hand into a half-arc and direct this half-arc so that it goes along the first vector (the first factor in the formula) and goes to the end of the second, then the thumb protruding upward will indicate the direction of the moment of torsion. Note also that before using this rule, you need to set the multiplied vectors so that they come out from the same point (their origins must match).
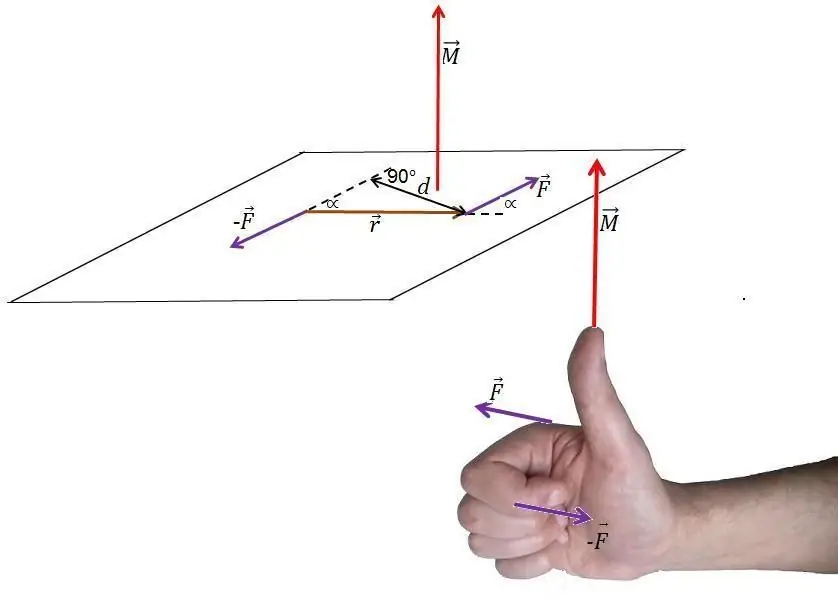
In the case of the figure in the previous paragraph, we can say, by applying the right hand rule, that the moment of force relative to the axis will be directed upwards, that is, towards us.
Besides the marked method of determining the direction of the vector M¯FO, there are two more. Here's them:
- The moment of torsion will be directed in such a way that if you look at the rotating lever from the end of its vector, the latter will move against the clock. It is generally accepted to consider this direction of the moment as positive when solving various kinds of problems.
- If you twist the gimlet clockwise, the torque will be directed towards the movement (deepening) of the gimlet.
All the above definitions are equivalent, so everyone can choose the one that is convenient for him.
So, it was found that the direction of the moment of force is parallel to the axis around which the corresponding lever rotates.
Angled force
Consider the picture below.
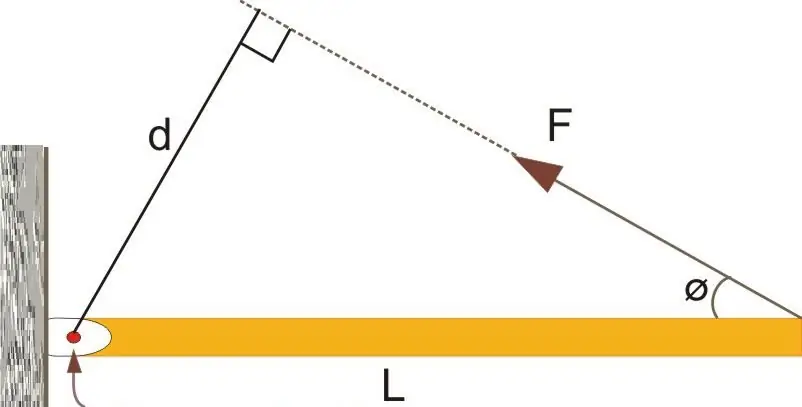
Here we also see a lever of length L fixed at a point (indicated by an arrow). A force F acts on it, however, it is directed at a certain angle Φ (phi) to the horizontal lever. The direction of the moment M¯FO in this case will be the same as in the previous figure (on us). To calculate the absolute value or modulus of this quantity, you must use the cross product property. According to him, for the example under consideration, you can write the expression: MFO=LFsin(180o -Φ) or, using the sine property, we rewrite:
MFO=LFsin(Φ).
The figure also shows a completed right-angled triangle, the sides of which are the lever itself (hypotenuse), the line of action of the force (leg) and the side of length d (the second leg). Given that sin(Φ)=d/L, this formula will take the form: MFO=dF. It can be seen that the distance d is the distance from the point of attachment of the lever to the line of action of the force, that is, d is the lever of force.
Both of the formulas considered in this paragraph, which follow directly from the definition of the moment of torsion, are useful in solving practical problems.
Torque units
Using the definition, it can be established that the value MFOshould be measured in newtons per meter (Nm). Indeed, in the form of these units, it is used in SI.
Note that Nm is a unit of work, which is expressed in joules, like energy. Nevertheless, joules are not used for the concept of the moment of force, since this value reflects precisely the possibility of implementing the latter. However, there is a connection with the unit of work: if, as a result of the action of the force F, the lever is completely rotated around its pivot point O, then the perfect work will be equal to A=MFO 2pi (2pi is the angle in radians that corresponds to 360o). In this case, the unit of torque MFO can be expressed in joules per radian (J/rad.). The latter, along with Hm, is also used in the SI system.
Varignon's theorem
At the end of the 17th century, the French mathematician Pierre Varignon, studying the equilibrium of systems with levers, first formulated the theorem, which now bears his last name. It is formulated as follows: the total moment of several forces is equal to the moment of the resulting one force, which is applied to a certain point relative to the same axis of rotation. Mathematically, it can be written as follows:
M¯1+M¯2 +…+M¯=M¯=d¯ ∑ i=1(F¯i)=d¯F¯.
This theorem is convenient to use to calculate the torsional moments in systems with multiple acting forces.
Next, we give an example of using the above formulas to solve problems in physics.
Wrench problem
One ofa vivid example of the importance of taking into account the moment of force is the process of unscrewing the nuts with a wrench. To unscrew the nut, you need to apply some torque. It is necessary to calculate how much force should be applied at point A to start unscrewing the nut, if this force at point B is 300 N (see the figure below).
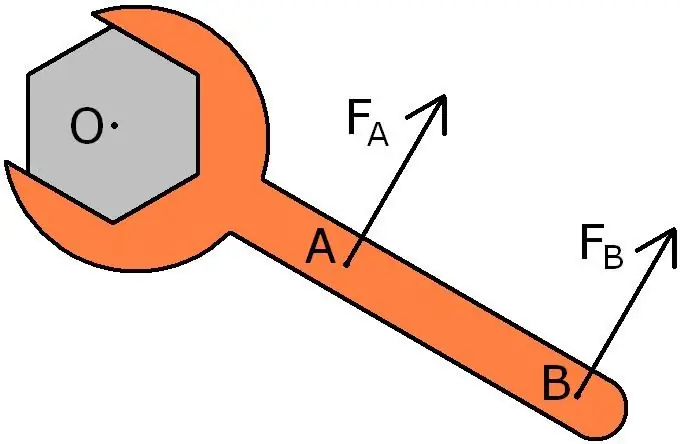
From the above figure, two important things follow: first, the distance OB is twice as large as OA; secondly, the forces FA and FBare directed perpendicular to the corresponding lever with the axis of rotation coinciding with the center of the nut (point O).
The torque moment for this case can be written in scalar form as follows: M=OBFB=OAFA. Since OB/OA=2, this equality will only hold if FA is 2 times greater than FB. From the condition of the problem, we obtain that FA=2300=600 N. That is, the longer the key, the easier it is to unscrew the nut.
Problem with two balls of different masses
The figure below shows a system that is in equilibrium. It is necessary to find the position of the fulcrum if the length of the board is 3 meters.

Since the system is in equilibrium, the sum of the moments of all forces is equal to zero. There are three forces acting on the board (the weights of the two balls and the reaction force of the support). Since the support force does not create a torque moment (the length of the lever is zero), there are only two moments created by the weight of the balls.
Let the equilibrium point be at a distance x fromedge containing a 100 kg ball. Then we can write the equality: M1-M2=0. Since the weight of the body is determined by the formula mg, then we have: m 1gx - m2g(3-x)=0. We reduce g and substitute the data, we get: 100x - 5(3-x)=0=> x=15/105=0.143 m or 14.3 cm.
Thus, in order for the system to be in equilibrium, it is necessary to establish a reference point at a distance of 14.3 cm from the edge where a ball of mass 100 kg will lie.






