Equilibrium problems in physics are considered in the statics section. One of the important forces that is present in any mechanical system in equilibrium is the reaction force of the support. What is it and how can it be calculated? These questions are detailed in the article.
What is the support reaction?
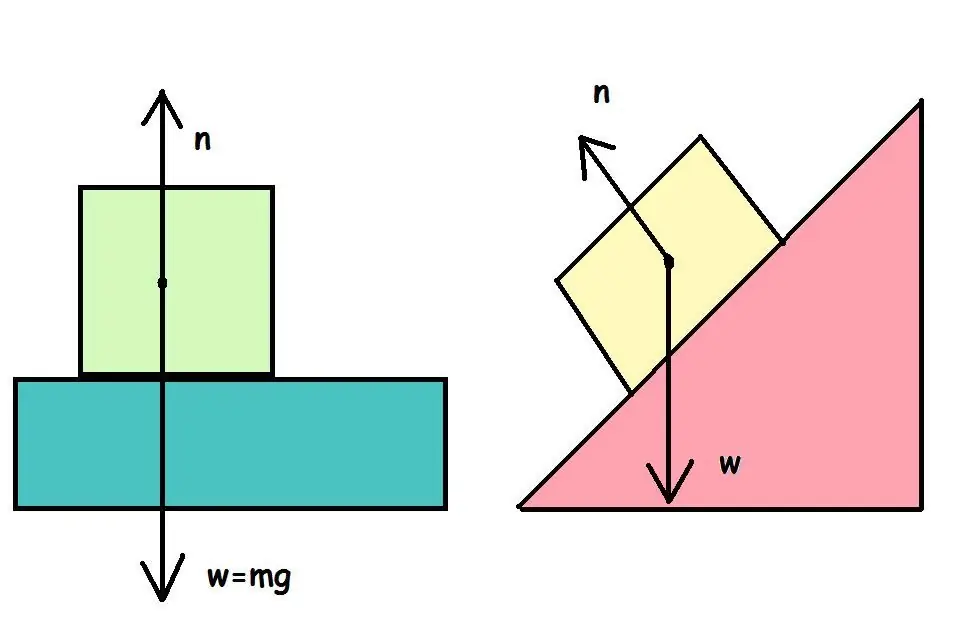
Each of us daily walks on the surface of the earth or on the floor, opens the door, sits on a chair, leaning on the table, climbs the landing. In all these cases, there is a reaction force of the support, which makes it possible to carry out the listed actions. This force in physics is denoted by the letter N and is called normal.
According to the definition, the normal force N is the force with which the support acts on the body in physical contact with it. It is called normal because it is directed along the normal (perpendicular) to the surface.
Normal support reaction always occurs as a response of an external force to one orother surface. To understand this, one should remember Newton's third law, which states that for every action there is a reaction. When the body presses on the support, the support acts on the body with the same modulus of force as the body on it.
The reason for the appearance of the normal force N

This reason lies in the strength of elasticity. If two solid bodies, regardless of the materials from which they are made, are brought into contact and slightly pressed against each other, then each of them begins to deform. Depending on the magnitude of the acting forces, the deformation changes. For example, if a weight of 1 kg is placed on a thin board, which is on two supports, then it will slightly bend. If this load is increased to 10 kg, the amount of deformation will increase.
The emerging deformation tends to restore the original shape of the body, while creating some elastic force. The latter affects the body and is called the support reaction.
If you look at a deeper, larger level, you can see that the elastic force appears as a result of the convergence of atomic shells and their subsequent repulsion due to the Pauli principle.
How to calculate the normal force?
It has already been said above that its modulus is equal to the resulting force directed perpendicular to the surface under consideration. This means that in order to determine the reaction of the support, it is first necessary to formulate an equation of motion, using Newton's second law, along a straight line that is perpendicular to the surface. Fromthis equation, you can find the value N.
Another way to determine the force N is to involve the physical condition of the balance of the moments of forces. This method is convenient to use if the system has rotation axes.
The moment of force is a value that is equal to the product of the acting force and the length of the lever relative to the axis of rotation. In a system in equilibrium, the sum of the moments of forces is always equal to zero. The last condition is used to find the unknown value N.

Note that if there is one support in the system (one axis of rotation), the normal force will always create a zero moment. Therefore, for such problems, the method described above should be applied using the Newtonian law to determine the support reaction.
There is no specific formula for calculating the force N. It is determined as a result of solving the corresponding equations of motion or equilibrium for the considered system of bodies.
Below we give examples of solving problems, where we show how to calculate the normal support reaction.
Inclined plane problem

The bar is at rest on an inclined plane. The mass of the beam is 2 kg. The plane is inclined to the horizon at an angle of 30o. What is the normal force N?
This task is not difficult. To get an answer to it, it is enough to consider all the forces that act along a line perpendicular to the plane. There are only two such forces: N and the projection of gravity Fgy. Since they act in different directions, Newton's equation for the system will take the form:
ma=N - Fgy
Because the beam is at rest, the acceleration is zero, so the equation becomes:
N=Fgy
The projection of the force of gravity on the normal to the plane is not difficult to find. From geometric considerations, we find:
N=Fgy=mgcos(α)
Substituting the data from the condition, we get: N=17 N.
Problem with two supports
A thin board is placed on two supports, the mass of which is insignificant. At 1/3 of the left support, a load of 10 kg was placed on the board. It is necessary to determine the reactions of the supports.
Since there are two supports in the problem, to solve it, you can use the equilibrium condition through the moments of forces. To do this, we first assume that one of the supports is the axis of rotation. For example, right. In this case, the moment equilibrium condition will take the form:
N1L - mg2/3L=0
Here L is the distance between the supports. From this equality it follows that the reaction of N1left support is equal to:
N1=2/3mg=2/3109, 81=65, 4 N.
Similarly, we find the reaction of the right support. The moment equation for this case is:
mg1/3L - N2L=0.
From where we get:
N2=1/3mg=1/3109, 81=32.7 N.
Note that the sum of the found reactions of the supports is equal to the gravity of the load.






