One of the main tasks of the analysis of dynamic control systems is the solution of the problem of their stability. Their stability is one of the most important characteristics of the management concept. A system is considered unstable if it does not return to its original position, but continues to oscillate after it has undergone some change at the input, or is under the influence of an unwanted perturbation.
Definition of the main concept
According to the concept of system stability, the state of its equilibrium is due to the absence of the impact of disturbing factors on it. In this situation, the difference between the set and actual state tends to zero. Stability is its ability to return to its original state of equilibrium after the perturbation that led to its violation has ended. An unstable system, due to the impact of a disturbance, moves away from the equilibrium state or oscillates, the amplitude of which graduallyrising.

Stability conditions
For the stability of a system with constant time, the following two conditions must be met:
- She will create a limited output for each input; if there is no input, the output must be zero, regardless of any initial conditions.
- The stability of the system can be called absolute or relative stability. The presented term is used in relation to a study in which certain quantities are compared, their operating conditions. Stability is the end result created by the result.
If the output of a system is infinite even when a finite input is applied to it, then it will be said to be unstable, i.e., inherently stable, it has a bounded termination when a bounded start is applied to itself.
In this case, the input is understood as various points of application of the influence of the external environment on the system. The output is the final product of its activity, which is in the form of the transformed input data.
In a continuous linear time system, the stability condition can be written for a specific impulse response.
When it is discrete, the stability index can also be written for a specific impulse response.
For an unstable condition in both continuous and bounded systems, these expressions will be infinite.
Types of stability and disturbances
Under staticThe stability of the system is understood as its ability to ensure the restoration of the original (or close to the original) regime after a small perturbation. Under the concept presented in this context, they consider a fluctuation that affects its behavior, regardless of where the surge or fall appears, and what their magnitude is. Based on this, these regimes, which are close to the initial one, allow us to consider it as linear.
Dynamic stability of systems is the ability of the latter to restore the initial state after a large disturbance.
Under a large fluctuation is understood such a movement, the nature of the influence of which and its corresponding behavior determine the time of existence, the magnitude and place of its occurrence.
Based on this, the system in this range is defined as non-linear.
Criteria for determining sustainability
The main condition for the stability of a linear system is not the nature of the perturbation, but its structure. It is believed that this stability "in the small" is determined if its boundaries are not established. Stability "in the big" is determined by the limits and the correspondence of real deviations to these established limits.
To determine the stability of the system, the following criteria are used:
- root criterion;
- Stodola criterion;
- Hurwitz criterion;
- Nyquist criterion;
- Mikhailov criterion and others
The root criterion and Stodola's evaluation technique are used to determine the stability of individual linksand open systems. The Hurwitz criterion is algebraic and allows determining the stability of closed systems without delay. The Nyquist and Mikhailov criteria are frequency ones. They are used to determine the stability of closed systems based on their frequency response.

Root criterion
It allows you to determine the stability of the system, based on the form of the transfer function. Its behavior properties are described by a characteristic polynomial (the denominator of the transfer function). If we equate the denominator to zero, the roots of the resulting equation will allow us to determine the degree of stability.
According to this criterion, the linear system will be stable if all the roots of the equation are in the left half-plane. If at least one of them is located on the stability boundary, it will also be at the limit. If at least one of them is in the right half-plane, the system can be considered unstable.
Stodola Criterion
It follows from the root definition. In accordance with the Stodola criterion, a linear system can be considered stable if all coefficients of the polynomial are positive.
Hurwitz criterion
This criterion is used for the characteristic polynomial of a closed system. According to this technique, a sufficient condition for stability is the fact that the value of the determinant and all principal diagonal minors of the matrix is greater than zero. If at least one of them is equalzero, it is considered on the stability boundary. If there is at least one negative determinant, it should be considered unstable.
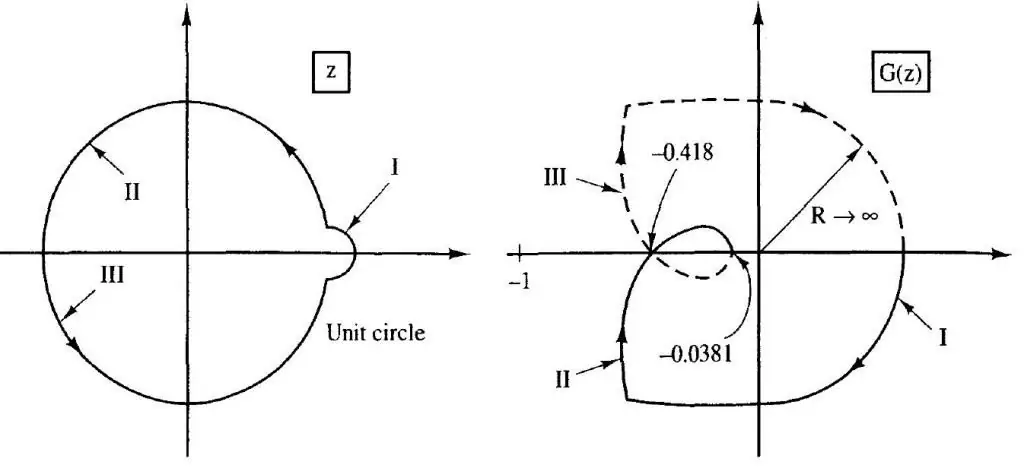
Nyquist criterion
This technique is based on the construction of a curve that connects the ends of a vector of a variable that displays the transfer function. The formulation of the criterion is as follows: a closed system is considered stable if the function curve does not enclose a point with coordinates (-1, j0) on the complex plane.
Financial Soundness System
Financial resilience is the state in which the system, i.e. key markets and institutions, is resilient to economic shocks and ready to smoothly perform its core functions of cash flow intermediation, risk management and payment arrangements.
Because of the mutual dependency relationship of providing interpretation (both vertically and horizontally), the analysis must cover the entire financial intermediation system. In other words, in addition to the banking sector, it is also necessary to analyze non-banking institutions that are involved in intermediation in one form or another. These include numerous types of institutions, including brokerage firms, investment funds, insurers, and other (various) entities. When analyzing the system of financial stability, the degree to which the entire structure is able to withstand external and internal shocks is studied. Of course, shocks do not always lead to crises, but the unstable financial environment itselfon its own can hinder the he althy development of the economy.
Various theories identify the causes of financial instability. Their relevance may vary depending on the period and the countries involved in the scope of the analysis. Among the problematic factors affecting the entire financial system, the literature usually identifies the following:
- rapid liberalization of the financial sector;
- inadequate economic policy;
- Untargeted exchange rate mechanism;
- inefficient allocation of resources;
- weak oversight;
- Inadequate regulation of accounting and auditing.
Possible causes appear not only collectively, but also individually or in a random combination, so the analysis of financial stability is an extremely difficult task. The focus on individual industries distorts the big picture, so the issues must be considered in their complexity in the course of studying financial stability.

The process of analyzing the stability of the enterprise system takes place in several stages.
Initially, absolute and relative indicators of financial stability are evaluated and analyzed. At the second stage, the factors are distributed in accordance with their significance, their influence is qualitatively and quantitatively assessed.
Financial Strength Ratios of Enterprises
The financial condition of the company, its stability largely depends on the optimal structure of capital sources, that is, the ratio of debt to own resources, on the optimalstructure of the company's assets and, first of all, on the ratio of fixed and current assets, as well as the balance of funds and liabilities of the company.
Therefore, it is important to study the structure of sources of venture capital and assess the degree of financial stability and risk. For this purpose, the coefficients of system stability are used:
- coefficient of autonomy (independence) - the share of capital in the balance sheet;
- dependency ratio - the share of borrowed capital in the balance sheet;
- current debt ratio - the ratio of short-term financial liabilities to the balance sheet;
- financial stability ratio (long-term financial independence) - the ratio of capital and long-term debt to the balance sheet;
- debt coverage ratio (solvency ratio) - the ratio of capital to debt;
- financial leverage ratio (financial risk ratio) - the ratio of debt to capital.

The higher the level of indicators such as autonomy, financial stability, coverage of debt capital, the lower the level of another group of coefficients (dependence, current debt, long-term obligations to investors) and, accordingly, the stability of the company's financial condition. Financial leverage is also called financial leverage.






