The heat capacity of a gas is the amount of energy that a body absorbs when it is heated by one degree. Let's analyze the main characteristics of this physical quantity.

Definitions
The specific heat of a gas is the unit mass of a particular substance. Its units of measurement are J/(kg·K). The amount of heat that is absorbed by the body in the process of changing its state of aggregation is associated not only with the initial and final state, but also with the method of transition.

Department
The heat capacity of gases is divided by the value determined at constant volume (Cv), constant pressure (Cр).
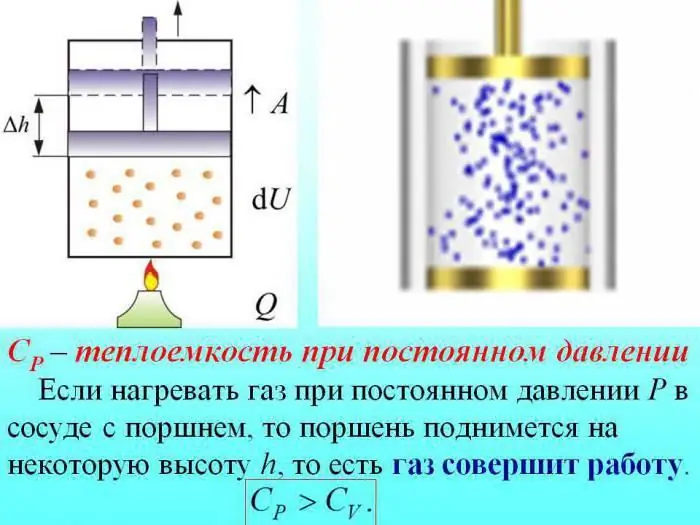
In the case of heating without changing the pressure, some heat is spent to produce the work of gas expansion, and part of the energy is spent to increase internal energy.
The heat capacity of gases at constant pressure is determined by the amount of heat that is spent on increasing internal energy.
Gas state: features, description
The heat capacity of an ideal gas is determined taking into account the fact that Сp-Сv=R. The latter quantity is called the universal gas constant. Its value corresponds to 8.314 J/(mol K).
When carrying out theoretical calculations of heat capacity, for example, describing the relationship with temperature, it is not enough to use only thermodynamic methods, it is important to arm yourself with elements of static physics.
The heat capacity of gases involves the calculation of the average value of the energy of the translational motion of some molecules. Such movement is summed up from the rotational and translational motion of the molecule, as well as from the internal vibrations of atoms.
In static physics, there is information that for each degree of freedom of rotational and translational motion, there is a quantity for a gas that is equal to half the universal gas constant.

Interesting facts
A particle of a monatomic gas is assumed to have three translational degrees of freedom, so the specific heat of a gas has three translational, two rotational, and one vibrational degrees of freedom. The law of their uniform distribution leads to equating the specific heat at a constant volume to R.
During the experiments, it was found that the heat capacity of a diatomic gas corresponds to the value R. Such a discrepancy between theory and practice is explained by the fact that the heat capacity of an ideal gas is associated with quantum effects, therefore, when making calculations, it is important to use statistics based on quantummechanics.
Based on the foundations of quantum mechanics, any system of particles that oscillate or rotate, including gas molecules, has only some discrete values of energy.
If the energy of thermal motion in the system is not enough to excite oscillations of a certain frequency, such motions do not contribute to the total heat capacity of the system.
As a result, a specific degree of freedom becomes "frozen", it is impossible to apply the law of equipartition to it.
The heat capacity of gases is an important characteristic of the state on which the functioning of the entire thermodynamic system depends.
The temperature at which the law of equipartition can be applied to the vibrational or rotational degree of freedom is characterized by quantum theory, connects the Planck constant with the Boltzmann constant.

Diatomic gases
The gaps between the rotational energy levels of such gases are a small number of degrees. The exception is hydrogen, in which the temperature value is determined by hundreds of degrees.
That is why the heat capacity of a gas at constant pressure is difficult to describe by the law of uniform distribution. In quantum statistics, when determining the heat capacity, it is taken into account that its oscillatory part, in the case of a decrease in temperature, quickly decreases and reaches zero.
This phenomenon explains the fact that at room temperature there is practically no vibrational part of the heat capacity, fordiatomic gas, it corresponds to the constant R.
The heat capacity of a gas at constant volume in the case of low temperature indicators is determined using quantum statistics. There is the Nernst principle, which is called the third law of thermodynamics. Based on its formulation, the molar heat capacity of a gas will decrease with decreasing temperature, tending to zero.

Features of solids
If the heat capacity of a mixture of gases can be explained using quantum statistics, then for a solid state of aggregation, thermal motion is characterized by slight fluctuations of particles near the equilibrium position.
Each atom has three vibrational degrees of freedom, therefore, in accordance with the equipartition law, the molar heat capacity of a solid can be calculated as 3nR, with n being the number of atoms in a molecule.
In practice, this number is the limit that the heat capacity of a solid body tends to at high temperatures.
Maximum can be obtained at ordinary temperatures for some elements, including metals. For n=1, the Dulong and Petit law is fulfilled, but for complex substances it is rather difficult to reach such a limit. Since the limit cannot be obtained in reality, decomposition or melting of the solid occurs.
History of quantum theory
The founders of quantum theory are Einstein and Debye at the beginning of the twentieth century. It is based on the quantization of oscillatory motions of atoms in a certaincrystal. In the case of low temperature indicators, the heat capacity of a solid body turns out to be directly proportional to the absolute value taken cubed. This relationship has been called Debye's law. As a criterion that allows you to distinguish between low and high temperature indicators, their comparison with the Debye temperature is taken.
This value is determined by the spectrum of vibrations of an atom in the body, therefore it seriously depends on the features of its crystal structure.
QD is a value that has a few hundred K, but, for example, in diamond it is much higher.
The conduction electrons make a significant contribution to the heat capacity of metals. To calculate it, the Fermi quantum statistics are used. The electronic conductivity for metal atoms is directly proportional to the absolute temperature. Since it is an insignificant value, it is taken into account only at temperatures tending to absolute zero.
Methods for determining heat capacity
The main experimental method is calorimetry. To carry out a theoretical calculation of heat capacity, statistical thermodynamics is used. It is valid for an ideal gas, as well as for crystalline bodies, is carried out on the basis of experimental data on the structure of matter.
Empirical methods for calculating the heat capacity of an ideal gas are based on the idea of the chemical structure, the contribution of individual groups of atoms to Ср.
For liquids, methods are also used that are based on the use of thermodynamiccycles that make it possible to pass from the heat capacity of an ideal gas to a liquid through the derivative of the temperature of the enthalpy of the evaporation process.
In the case of a solution, the calculation of the heat capacity as an additive function is not allowed, since the excess value of the heat capacity of the solution is basically significant.
To evaluate it, we need the molecular-statistical theory of solutions. The most difficult is the identification of the heat capacity of heterogeneous systems in thermodynamic analysis.

Conclusion
The study of heat capacity allows you to calculate the energy balance of processes occurring in chemical reactors, as well as in other chemical production apparatuses. In addition, this value is necessary for the selection of optimal types of coolants.
At present, the experimental determination of the heat capacity of substances for various temperature intervals - from low values to high values - is the main option for determining the thermodynamic characteristics of a substance. When calculating the entropy and enthalpy of a substance, heat capacity integrals are used. Information about the heat capacity of chemical reagents in a certain temperature range allows you to calculate the thermal effect of the process. Information on the heat capacity of solutions makes it possible to calculate their thermodynamic parameters at any temperature values within the analyzed interval.
For example, a liquid is characterized by the expenditure of part of the heat to change the value of potential energyreacting molecules. This value is called the "configuration" heat capacity, used to describe solutions.
It is difficult to conduct full-fledged mathematical calculations without taking into account the thermodynamic characteristics of a substance, its state of aggregation. That is why for liquids, gases, solids, such a characteristic as specific heat capacity is used, which makes it possible to characterize the energy parameters of a substance.






