It should be reminded from the very beginning, so as not to get confused later: there are numbers - there are 10 of them. From 0 to 9. There are numbers, and they consist of numbers. There are infinitely many numbers. Definitely more than the stars in the sky.
A mathematical expression is an instruction written using mathematical symbols, what actions need to be performed with numbers in order to get a result. Not to “reach” the desired result, as in statistics, but to find out exactly how many of them there were. But what happened and when - is no longer within the scope of interests of arithmetic. At the same time, it is important not to make a mistake in the sequence of actions, which is first - addition or multiplication? An expression in school is sometimes called an "example".

Addition and subtraction
What actions can be performed with numbers? There are two basic ones. This is addition and subtraction. All other actions are built on these two.
The simplest human action: take two piles of stones and mix them into one. This is addition. In order to get the result of such an action, you may not even know what addition is. It is enough just to take a bunch of stones from Petya and a bunch of stones from Vasya. Put it all together, count everything again. The new result of the sequential counting of stones from the new pile is the sum.
In the same way, you can not know what subtraction is, just take and divide a pile of stones into two parts or take a certain number of stones from a pile. So what is called the difference will remain in the heap. You can only take what is in the pile. Credit and other economic terms are not considered in this article.
In order not to count the stones every time, because it happens that there are a lot of them and they are heavy, they came up with mathematical operations: addition and subtraction. And for these actions they came up with a calculation technique.

The sum of any two numbers is stupidly memorized without any technique. 2 plus 5 equals seven. You can count on counting sticks, stones, fish heads - the result is the same. Put 2 sticks first, then 5, and then count everything together. There is no other way.
Those who are smarter, usually cashiers and students, memorize more, not only the sum of two digits, but also the sum of numbers. But most importantly, they can add numbers in their mind using different techniques. This is called the skill of mental counting.
To add numbers consisting of tens, hundreds, thousands and even larger digits, usespecial techniques - column addition or calculator. With a calculator, you can not even add numbers, and you don’t need to read further.
Column addition is a method that allows you to add large (multi-digit) numbers by learning only the results of adding digits. When adding a column, the corresponding decimal digits of two numbers are sequentially added (that is, actually two digits), if the result of adding two digits exceeds 10, then only the last digit of this sum is taken into account - units of the number, and 1.
is added to the sum of the following digits
Multiplication
Mathematicians like to group similar actions together to make calculations easier. So the operation of multiplication is a grouping of identical actions - addition of identical numbers. Any product N x M − is N operations of addition of numbers M. This is just a form of writing the addition of identical terms.
To calculate the product, the same method is used - first, the table of multiplication of digits against each other is stupidly memorized, and then the bitwise multiplication method is applied, which is called "in a column".

Which comes first, multiplication or addition?
Any mathematical expression is actually a record of the accountant "from the field" about the results of any actions. Let's say harvesting tomatoes:
- 5 adult workers picked 500 tomatoes each and met the quota.
- 2 schoolchildren did not go to math classes and helped adults: they picked 50 tomatoes each, did not meet the norm, ate 30 tomatoes, took a bite andspoiled another 60 tomatoes, 70 tomatoes were taken from the pockets of assistants. Why they took them with them into the field is unclear.
All the tomatoes were handed over to the accountant, he stacked them in piles.
Write the result of "harvesting" as an expression:
- 500 + 500 + 500 + 500 + 500 are bunches of adult workers;
- 50 + 50 are bunches of underage workers;
- 70 - taken from the pockets of schoolchildren (spoiled and bitten does not count towards the result).
Get an example for the school, a record of the performance record:
500 + 500 +500 +500 +500 + 50 +50 + 70=?;
Here you can apply grouping: 5 heaps of 500 tomatoes - this can be written through the multiplication operation: 5 ∙ 500.
Two piles of 50 - this can also be written through multiplication.
And one bunch of 70 tomatoes.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70=?
And what to do in the example first - multiplication or addition? So, you can only add tomatoes. You can't put 500 tomatoes and 2 piles together. They don't stack. Therefore, at first it is always necessary to bring all records to the basic addition operations, that is, first of all, to calculate all the grouping-multiplication operations. In very simple words, multiplication is performed first, and addition only then. If you multiply 5 piles of 500 tomatoes each, you get 2500 tomatoes. And then they can already be stacked with tomatoes from other piles.
2500 + 100 + 70=2 670
When a child learns mathematics, it is necessary to convey to him that this is a tool used in everyday life. Mathematical expressions are, in fact (in the simplest version of elementary school), warehouse records about the amount of goods, money (very easily perceived by schoolchildren), and other items.
Accordingly, any work is the sum of the contents of a certain number of identical containers, boxes, piles containing the same number of items. And that first multiplication, and then addition, that is, first began to calculate the total number of items, and then add them together.
Division
The division operation is not considered separately, it is the inverse of multiplication. It is necessary to distribute something among the boxes, so that all boxes have the same given number of items. The most direct analogue in life is packaging.

Parentheses
Brackets are of great importance in solving examples. Parentheses in arithmetic - a mathematical sign used to regulate the sequence of calculations in an expression (example).
Multiplication and division take precedence over addition and subtraction. And parentheses take precedence over multiplication and division.
Whatever is in parentheses is evaluated first. If the brackets are nested, then the expression in the inner brackets is evaluated first. And this is an immutable rule. As soon as the expression in the brackets is evaluated, the brackets disappear and a number appears in their place. Options for expanding brackets with unknowns are not considered here. This is done until all of them disappear from the expression.
((25-5): 5 + 2): 3=?
- It's like candy boxes in a big bag. First you need to open all the boxes and pour them into a large bag: (25 - 5) u003d 20. Five candies from the box were immediately sent to the excellent student Lyuda, who was sick and did not participate in the holiday. The rest of the candy is in the bag!
- Then tie the candies into bundles of 5 pieces: 20: 5=4.
- Then add 2 more bunches of sweets to the bag so that you can divide it into three children without a fight. The signs of division by 3 are not considered in this article.
(20: 5 + 2): 3=(4 +2): 3=6: 3=2
Total: three children each with two bundles of sweets (one bundle per hand), 5 sweets per bundle.
If you calculate the first parentheses in the expression and rewrite everything again, the example will become shorter. The method is not fast, with a lot of paper consumption, but surprisingly effective. At the same time trains mindfulness when rewriting. The example is brought to a view when there is only one question left, first multiplication or addition without parentheses. That is, to such a form, when there are no longer brackets. But the answer to this question is already there, and there is no point in discussing which comes first - multiplication or addition.
Cherry on the cake
And finally. The rules of the Russian language do not apply to a mathematical expression - read and execute from left to right:
5 - 8 + 4=1;
This simple example can bring a child to hysterics or spoil his mother's evening. Because she will have to explain to the second grader that there are negative numbers. Or destroy the authority of “MaryaVanovna”, who said that: “You need to go from left to right and in order.”
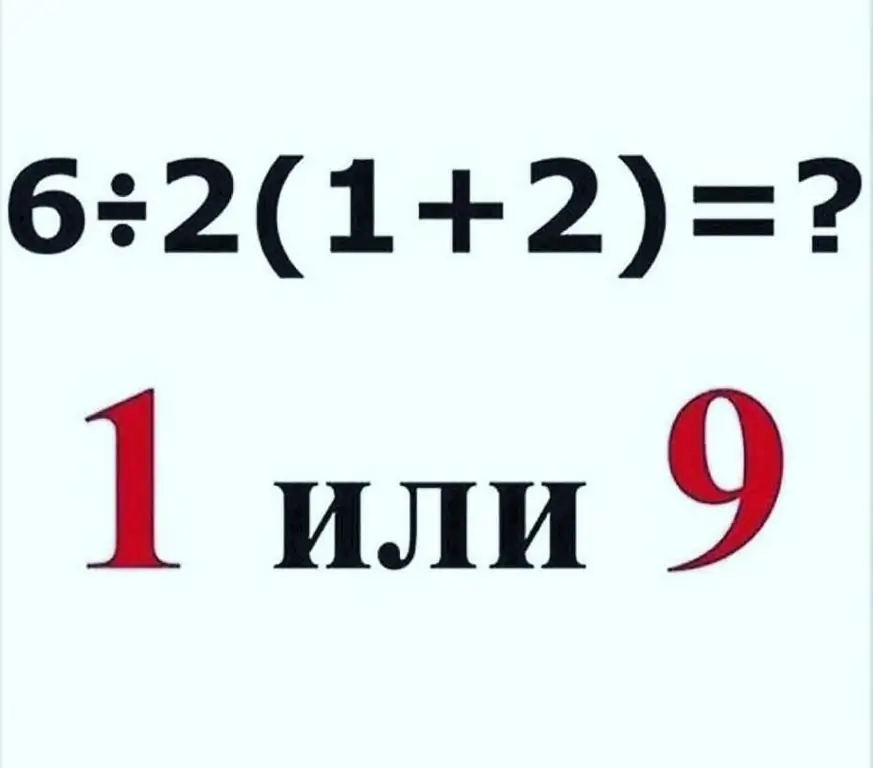
Quite cherry
An example is circulating on the Web that causes difficulties for adult uncles and aunts. It's not quite on the topic at hand, what comes first - multiplication or addition. It seems to be about the fact that you first perform the action in brackets.
The sum does not change from the rearrangement of the terms, nor from the rearrangement of the factors. You just need to write the expression in such a way that it would not be painfully embarrassing later.
6: 2 ∙ (1+2)=6 ∙ ½ ∙ (1+2)=6 ∙ ½ ∙ 3=3 ∙ 3=9
That's all for sure now!






