Every high school student knows about such spatial figures as a ball, cylinder, cone, pyramid and prism. From this article you will learn about what a triangular prism is and what properties it is characterized by.
Which figure will we consider in the article?
The triangular prism is the simplest representative of the class of prisms, which has fewer sides, vertices and edges than any other similar spatial figure. This prism is formed by two triangles, which can have an arbitrary shape, but which must necessarily be equal to each other and be in parallel planes in space, and three parallelograms, which are not equal to each other in the general case. For clarity, the described figure is shown below.

How can I get a triangular prism? It's very simple: you should take a triangle and transfer it to some vector in space. Then connect the identical vertices of the two triangles with segments. So we get the frame of the figure. If we now imagine that this frame limits the solid sides, then we getdepicted three-dimensional figure.
What elements does the prism under study consist of?
A triangular prism is a polyhedron, that is, it is formed by several intersecting faces or sides. It was indicated above that it has five such sides (two triangular and three quadrangular). Triangular sides are called bases, while parallelograms are side faces.
Like any polyhedron, the studied prism has vertices. Unlike a pyramid, the vertices of any prism are equal. The triangular figure has six of them. All of them belong to both bases. Two base edges and one side edge intersect at each vertex.
If we add the number of vertices to the number of sides of the figure, and then subtract the number 2 from the resulting value, then we will get the answer to the question of how many edges the prism under consideration has. There are nine of them: six limit the bases, and the remaining three separate the parallelograms from each other.
Shape types
The sufficiently detailed description of a triangular prism given in the previous paragraphs corresponds to several types of figures. Consider their classification.
The studied prism can be inclined and straight. The difference between them lies in the type of side faces. In a straight prism they are rectangles, and in an oblique prism they are general parallelograms. Shown below are two prisms with triangular bases, one straight and one oblique.

Unlike an inclined prism, a straight prism has all dihedral angles between the bases andsides are 90°. What does the last fact mean? That the height of a triangular prism, that is, the distance between its bases, in a straight figure is equal to the length of any side edge. For an oblique figure, the height is always less than the length of any of its side edges.
Prism with a triangular base can be irregular and correct. If its bases are triangles with equal sides, and the figure itself is straight, then it is called regular. A regular prism has a fairly high symmetry, including reflection planes and axes of rotation. For a regular prism, formulas for calculating its volume and surface area of the faces will be given below. So, in order.
Area of a triangular prism
Before proceeding to obtain the corresponding formula, we present the sweep of the correct prism.
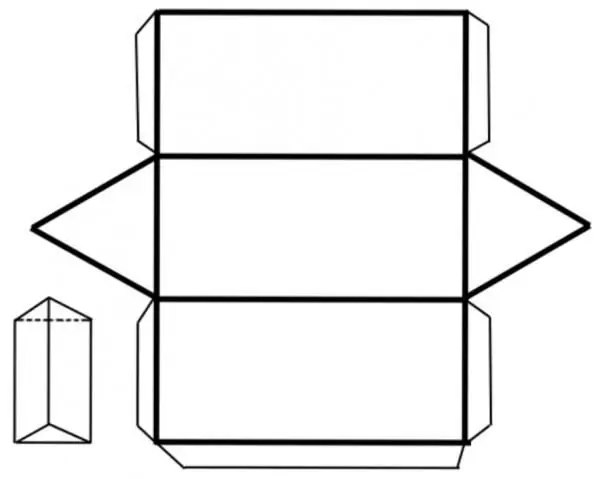
It is clear that the area of a figure can be calculated by adding three areas of identical rectangles and two areas of equal triangles with the same sides. Let's denote the height of the prism by the letter h, and the side of its triangular base - by the letter a. Then for the area of triangle S3 we have:
S3=√3/4a2
This expression is obtained by multiplying the height of a triangle by its base and then dividing the result by 2.
For the area of the rectangle S4we get:
S4=ah
Adding the areas of all sides, we get the total surface area of the figure:
S=2 S3+ 3S4=√3/2a2+ 3ah
Here the first term reflects the area of the bases, and the second is the area of the lateral surface of the triangular prism.
Recall that this formula is valid only for a regular figure. In the case of an incorrect inclined prism, the calculation of the area should be carried out in stages: first determine the areas of the bases, and then the lateral surface. The latter will be equal to the product of the side edge and the perimeter of the cut perpendicular to the side faces.
The volume of the figure

The volume of a triangular prism can be calculated using the formula common to all figures of this class. It looks like:
V=So h
In the case of a regular triangular prism, this formula will take the following specific form:
V=√3/4a2 h
If the prism is irregular, but straight, then instead of the area of the base, you should substitute the corresponding area for the triangle. If the prism is inclined, then, in addition to determining the area of \u200b\u200bthe base, its height should also be calculated. As a rule, trigonometric formulas are used for this, if the dihedral angles between the sides and the bases are known.






