The pentagonal prism in solving problems in geometry is much less common than such prisms as triangular, quadrangular or hexagonal. Nevertheless, it is useful to review the basic properties of this shape, as well as learn how to draw it.
What is a pentagonal prism?
This is a three-dimensional figure, the bases of which are pentagons, and the sides are parallelograms. If each of these parallelograms is perpendicular to the parallel bases, then such a prism is called rectangular. The lateral surface of a rectangular pentagonal prism is composed of five rectangles. Moreover, the side adjacent to the base of each of them is equal to the corresponding length of the side of the pentagon.

If the pentagon is regular, that is, all its sides and angles are equal to each other, then such a rectangular prism is called regular. Further in the article we will consider the properties of this particular figure.
Prism elements
For her, as for any prism,the following elements are characteristic:
- faces or sides are parts of planes that bound a figure in space;
- tops - points of intersection of three sides;
- ribs - segments of the intersection of two sides of the figure.
The numbers of all named elements are related to each other by the following equality:
Number of edges=number of vertices + number of faces - 2
This expression is called the Euler formula for the polyhedron.
In a pentagonal prism, the number of sides is seven (two bases + five rectangles). The number of peaks is 10 (five for each base). The number of edges in this case will be:
Number of ribs=10 + 7 - 2=15
Ten edges belong to the bases of the prism, and five edges are formed by rectangles.
How to draw a pentagonal prism?
The answer to this question depends on the specific task. If it is necessary to draw an arbitrary prism, then any pentagon should be drawn. After that, draw five parallel segments of equal length from each vertex of the pentagon. Then, connect the upper ends of the segments. The result is a pentagonal arbitrary prism.
If it is necessary to draw a regular prism, then the whole complexity of the task comes down to obtaining a regular pentagon. There are several ways to draw this polygon. Here we will consider only two ways.

The first way is to draw a circle with a compass. Then an arbitrary diameter is drawncircle and five angles are counted from it using a protractor at 72o(572o=360o). When counting each angle, a notch is made on the circle. To build a rectangle, it remains to connect the marked notches with straight segments.
The second method involves using only a compass and a ruler. It is somewhat complex in comparison with the previous one. Below is a video that explains in detail each step of this build.

Note that it is easy to draw a pentagon if you connect the ends of the star. If it is not necessary to draw an exactly regular pentagon, then you can use the hand-drawn star method.
As soon as the pentagon is drawn, it is necessary to draw five identical parallel segments from each of its vertices and connect their vertices. The result is a pentagonal prism.
Shape area
Now consider how to find the area of a pentagonal prism. The figure below shows its development. It can be seen that the required area is formed by two identical pentagons and five rectangles equal to each other.
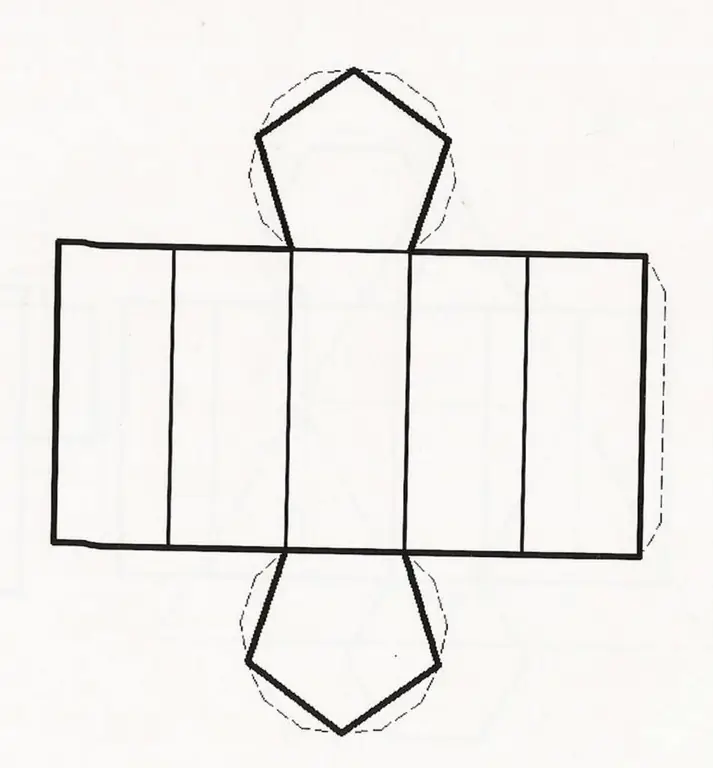
The area of the entire surface of the figure is expressed by the formula:
S=2So+ 5Sp
Here the indices o and p mean the base and the rectangle, respectively. Let's denote the length of the side of the pentagon as a, and the height of the figure as h. Then for the rectangle we write:
Sp=ah
To calculate the area of a pentagon,use the universal formula:
S=n/4a2ctg(pi/n)
Where n is the number of sides of the polygon. Substituting n=5, we get:
S5=5/4a2ctg(pi/5) ≈ 1, 72a 2
The accuracy of the resulting equality is 3 decimal places, which is quite enough to solve any problems.
Now it remains to find the sum of the obtained areas of the base and the side surface. We have:
S=21, 72a2 + 5ah=3, 44a2 + 5a h
It should be remembered that the resulting formula is valid only for a rectangular prism. In the case of an oblique figure, the area of its lateral surface is found based on the knowledge of the perimeter of the cut, which must be perpendicular to all parallelograms.

The volume of the figure
The formula for calculating the volume of a pentagonal prism is no different from a similar expression for any other prism or cylinder. The volume of a figure is equal to the product of its height and the area of the base:
V=Soh
If the prism in question is rectangular, then its height is the length of the edge formed by the rectangles. The area of a regular pentagon has been calculated above with high accuracy. Substitute this value into the formula for volume and get the necessary expression for a regular pentagonal prism:
V=1, 72a2h
Thus, calculating volume and surface areaa pentagonal regular prism is possible if the side of the base and the height of the figure are known.






