Quantum mechanics deals with the objects of the microworld, with the most elementary constituents of matter. Their behavior is determined by probabilistic laws, manifested in the form of corpuscular-wave duality - dualism. In addition, an important role in their description is played by such a fundamental quantity as the physical action. The natural unit that sets the quantization scale for this quantity is Planck's constant. It also governs one of the fundamental physical principles - the uncertainty relation. This seemingly simple inequality reflects the natural limit to which nature can answer some of our questions simultaneously.
Prerequisites for deriving the uncertainty relation
The probabilistic interpretation of the wave nature of particles, introduced into science by M. Born in 1926, clearly indicated that classical ideas about motion are inapplicable to phenomena on the scales of atoms and electrons. At the same time, some aspects of the matrixmechanics, created by W. Heisenberg as a method of mathematical description of quantum objects, required the elucidation of their physical meaning. So, this method operates with discrete sets of observables, represented as special tables - matrices, and their multiplication has the property of non-commutativity, in other words, A×B ≠ B×A.

As applied to the world of microparticles, this can be interpreted as follows: the result of operations to measure parameters A and B depends on the order in which they are performed. In addition, inequality means that these parameters cannot be measured simultaneously. Heisenberg investigated the question of the relationship between measurement and the state of a microobject, setting up a thought experiment to achieve the limit of accuracy of simultaneously measuring such particle parameters as momentum and position (such variables are called canonically conjugate).
Formulation of the uncertainty principle
The result of Heisenberg's efforts was the conclusion in 1927 of the following limitation on the applicability of classical concepts to quantum objects: with increasing accuracy in determining the coordinate, the accuracy with which momentum can be known decreases. The reverse is also true. Mathematically, this limitation was expressed in the uncertainty relation: Δx∙Δp ≈ h. Here x is the coordinate, p is the momentum, and h is Planck's constant. Heisenberg later refined the relationship: Δx∙Δp ≧ h. The product of "deltas" - spreads in the value of coordinate and momentum - having the dimension of action cannot be less than the "smallestportion" of this quantity is Planck's constant. As a rule, the reduced Planck constant ħ=h/2π is used in formulas.
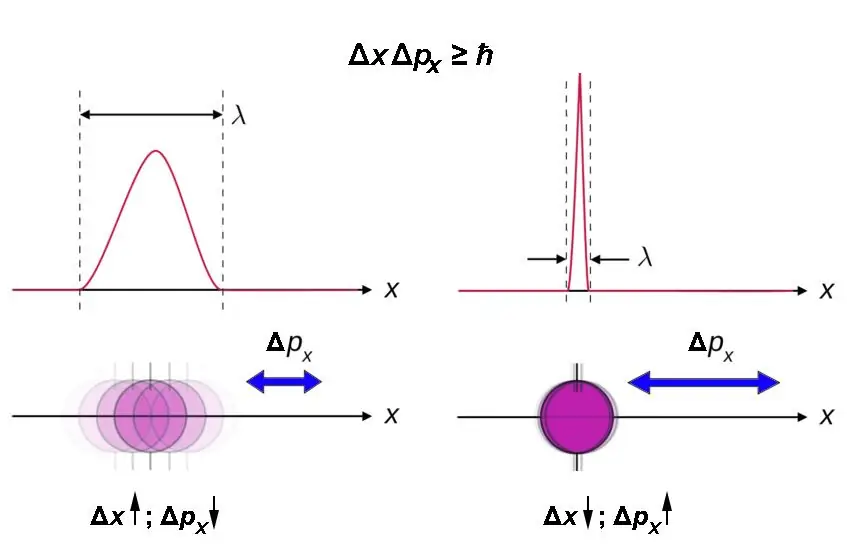
The above ratio is generalized. It must be taken into account that it is valid only for each pair of coordinate - component (projection) of the impulse on the corresponding axis:
- Δx∙Δpx ≧ ħ.
- Δy∙Δpy ≧ ħ.
- Δz∙Δpz ≧ ħ.
The Heisenberg uncertainty relation can be briefly expressed as follows: the smaller the region of space in which a particle moves, the more uncertain is its momentum.
Thought experiment with gamma microscope
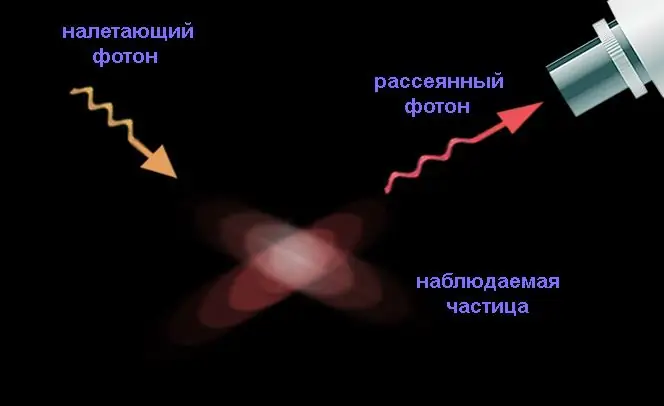
As an illustration of the principle he discovered, Heisenberg considered an imaginary device that allows you to measure the position and speed (and through it the momentum) of an electron arbitrarily accurately by scattering a photon on it: after all, any measurement is reduced to an act of particle interaction, without this a particle not detectable at all.
To increase the accuracy of measuring the coordinates, a shorter-wavelength photon is needed, which means that it will have a large momentum, a significant part of which will be transferred to the electron during scattering. This part cannot be determined, since the photon is scattered on the particle in a random way (despite the fact that the momentum is a vector quantity). If the photon is characterized by a small momentum, then it has a large wavelength, therefore, the electron coordinate will be measured with a significant error.
The fundamental nature of the uncertainty relation
In quantum mechanics, Planck's constant, as noted above, plays a special role. This fundamental constant is included in almost all equations of this branch of physics. Its presence in the Heisenberg uncertainty ratio formula, firstly, indicates the extent to which these uncertainties manifest themselves, and, secondly, it indicates that this phenomenon is not associated with the imperfection of the means and methods of measurement, but with the properties of matter itself and is universal.
It may seem that in reality the particle still has specific values of speed and coordinate at the same time, and the act of measurement introduces irremovable interference in their establishment. However, it is not. The motion of a quantum particle is associated with the propagation of a wave, the amplitude of which (more precisely, the square of its absolute value) indicates the probability of being at a particular point. This means that a quantum object has no trajectory in the classical sense. We can say that it has a set of trajectories, and all of them, according to their probabilities, are carried out when moving (this is confirmed, for example, by experiments on electron wave interference).

The absence of a classical trajectory is equivalent to the absence of such states in a particle in which the momentum and coordinates would be characterized by exact values simultaneously. Indeed, it is meaningless to speak of the lengthwave at some point”, and since the momentum is related to the wavelength by the de Broglie relation p=h / λ, a particle with a certain momentum does not have a certain coordinate. Accordingly, if the micro-object has an exact coordinate, the momentum becomes completely indefinite.
Uncertainty and action in micro and macro worlds
The physical action of a particle is expressed in terms of the phase of the probability wave with the coefficient ħ=h/2π. Consequently, the action, as a phase that controls the amplitude of the wave, is associated with all possible trajectories, and the probabilistic uncertainty in relation to the parameters that form the trajectory is fundamentally irremovable.
Action is proportional to position and momentum. This value can also be represented as the difference between the kinetic and potential energy, integrated over time. In short, action is a measure of how the motion of a particle changes over time, and it depends, in part, on its mass.
If the action significantly exceeds Planck's constant, the most probable is the trajectory determined by such a probability amplitude, which corresponds to the smallest action. The Heisenberg uncertainty relation briefly expresses the same thing if it is modified to take into account that the momentum is equal to the product of the mass m and the velocity v: Δx∙Δvx ≧ ħ/m. It immediately becomes clear that with an increase in the mass of the object, the uncertainties become less and less, and when describing the motion of macroscopic bodies, classical mechanics is quite applicable.

Energy and time
The uncertainty principle is also valid for other conjugate quantities representing the dynamic characteristics of particles. These, in particular, are energy and time. They also, as already noted, determine the action.
The energy-time uncertainty relation has the form ΔE∙Δt ≧ ħ and shows how the accuracy of the particle energy value ΔE and the time interval Δt over which this energy must be estimated are related. Thus, it cannot be argued that a particle can have a strictly defined energy at some exact moment in time. The shorter the period Δt we consider, the larger the particle energy will fluctuate.
An electron in an atom
It is possible to estimate, using the uncertainty relation, the width of the energy level, for example, of a hydrogen atom, that is, the spread of the electron energy values in it. In the ground state, when the electron is at the lowest level, the atom can exist indefinitely, in other words, Δt→∞ and, accordingly, ΔE takes on a zero value. In the excited state, the atom stays only for some finite time of the order of 10-8 s, which means that it has an energy uncertainty ΔE=ħ/Δt ≈ (1, 05∙10- 34 J∙s)/(10-8 s) ≈ 10-26 J, which is about 7∙10 -8 eV. The consequence of this is the uncertainty of the frequency of the emitted photon Δν=ΔE/ħ, which manifests itself as the presence of some spectral linesblur and the so-called natural width.
We can also by simple calculations, using the uncertainty relation, estimate both the width of the dispersion of the coordinates of an electron passing through a hole in an obstacle, and the minimum dimensions of an atom, and the value of its lowest energy level. The ratio derived by W. Heisenberg helps in solving many problems.

Philosophical understanding of the uncertainty principle
The presence of uncertainties is often erroneously interpreted as evidence of complete chaos allegedly reigning in the microcosm. But their ratio tells us something completely different: always speaking in pairs, they seem to impose a completely natural restriction on each other.
The ratio, mutually linking the uncertainties of dynamic parameters, is a natural consequence of the dual - corpuscular-wave - nature of matter. Therefore, it served as the basis for the idea put forward by N. Bohr with the aim of interpreting the formalism of quantum mechanics - the complementarity principle. We can obtain all information about the behavior of quantum objects only through macroscopic instruments, and we are inevitably forced to use the conceptual apparatus developed within the framework of classical physics. Thus, we have the opportunity to investigate either the wave properties of such objects, or the corpuscular ones, but never both at the same time. By virtue of this circumstance, we must consider them not as contradictory, but as complementary to each other. A simple formula for the uncertainty relationpoints us to the boundaries near which it is necessary to include the principle of complementarity for an adequate description of quantum mechanical reality.






