In practice, tasks often arise that require the ability to build sections of geometric shapes of various shapes and find the area of sections. In this article, we will look at how important sections of a prism, pyramid, cone and cylinder are built, and how to calculate their areas.
3D figures
From stereometry it is known that a three-dimensional figure of absolutely any type is limited by a number of surfaces. For example, for such polyhedra as a prism and a pyramid, these surfaces are the polygonal sides. For a cylinder and a cone, we are talking about surfaces of revolution of cylindrical and conical figures.
If we take a plane and arbitrarily intersect the surface of a three-dimensional figure, we will get a section. Its area is equal to the area of the part of the plane that will be inside the volume of the figure. The minimum value of this area is zero, which is realized when the plane touches the shape. For example, a section that is formed by a single point is obtained if the plane passes through the top of a pyramid or cone. The maximum value of the cross-sectional area depends onthe relative position of the figure and the plane, as well as the shape and size of the figure.
Below, we will consider how to calculate the area of formed sections for two figures of revolution (cylinder and cone) and two polyhedra (pyramid and prism).
Cylinder
Circular cylinder is a figure of rotation of a rectangle around any of its sides. The cylinder is characterized by two linear parameters: base radius r and height h. Below is a schematic representation of what a circular straight cylinder looks like.
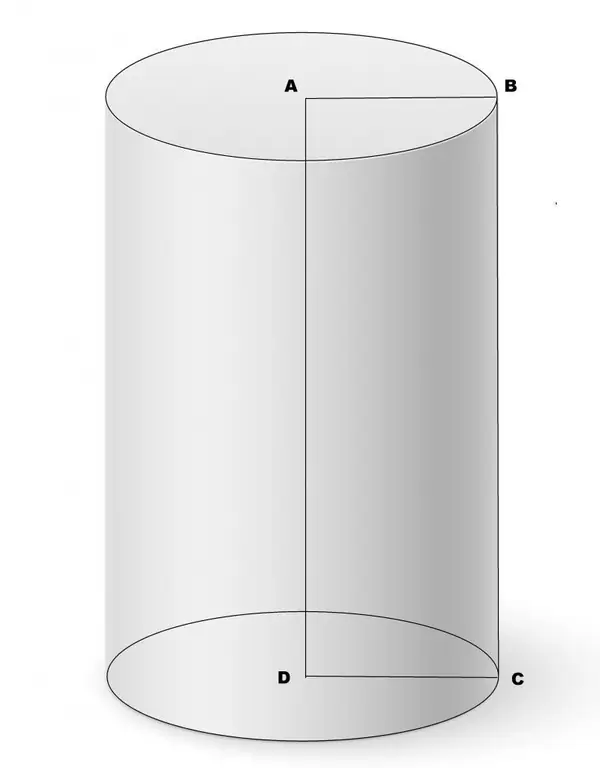
There are three important section types for this figure:
- round;
- rectangular;
- elliptical.
Elliptical is formed as a result of the plane intersecting the side surface of the figure at some angle to its base. Round is the result of the intersection of the cutting plane of the side surface parallel to the base of the cylinder. Finally, a rectangular one is obtained if the cutting plane is parallel to the axis of the cylinder.
Circular area is calculated by the formula:
S1=pir2
The area of the axial section, i.e. rectangular, which passes through the axis of the cylinder, is defined as follows:
S2=2rh
Cone sections
A cone is a figure of rotation of a right triangle around one of the legs. The cone has one top and a round base. Its parameters are also radius r and height h. An example of a paper cone is shown below.

There are several types of conic sections. Let's list them:
- round;
- elliptical;
- parabolic;
- hyperbolic;
- triangular.
They replace each other if you increase the angle of inclination of the secant plane relative to the round base. The easiest way is to write down the formulas for the cross-sectional area of \u200b\u200bcircular and triangular.
A circular section is formed as a result of the intersection of a conical surface with a plane that is parallel to the base. For its area, the following formula is valid:
S1=pir2z2/h 2
Here z is the distance from the top of the figure to the formed section. It can be seen that if z=0, then the plane passes only through the vertex, so the area S1 will be equal to zero. Since z < h, the area of the section under study will always be less than its value for the base.
Triangular is obtained when the plane intersects the figure along its axis of rotation. The shape of the resulting section will be an isosceles triangle, the sides of which are the diameter of the base and two generators of the cone. How to find the cross-sectional area of a triangular? The answer to this question will be the following formula:
S2=rh
This equality is obtained by applying the formula for the area of an arbitrary triangle through the length of its base and height.
Prism sections
Prism is a large class of figures that are characterized by the presence of two identical polygonal bases parallel to each other,connected by parallelograms. Any section of a prism is a polygon. In view of the diversity of the figures under consideration (oblique, straight, n-gonal, regular, concave prisms), the variety of their sections is also great. Below, we consider only some special cases.
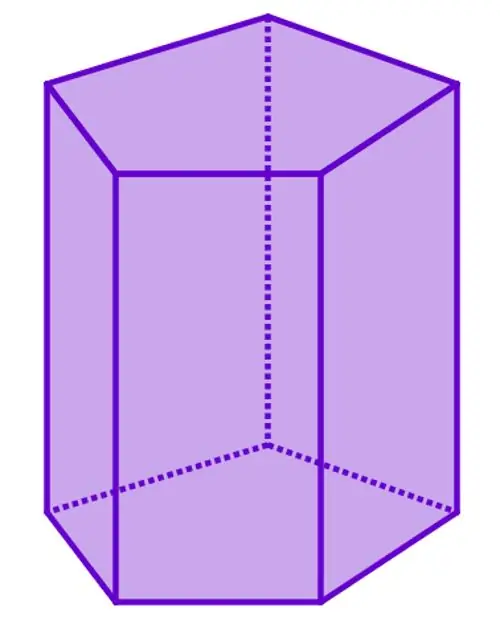
If the cutting plane is parallel to the base, then the cross-sectional area of the prism will be equal to the area of this base.
If the plane passes through the geometric centers of the two bases, that is, it is parallel to the side edges of the figure, then a parallelogram is formed in the section. In the case of straight and regular prisms, the considered section view will be a rectangle.
Pyramid
Pyramid is another polyhedron that consists of an n-gon and n triangles. An example of a triangular pyramid is shown below.

If the section is drawn by a plane parallel to the n-gonal base, then its shape will be exactly equal to the shape of the base. The area of such a section is calculated by the formula:
S1=So(h-z)2/h 2
Where z is the distance from the base to the section plane, So is the area of the base.
If the cutting plane contains the top of the pyramid and intersects its base, then we get a triangular section. To calculate its area, you must refer to the use of the appropriate formula for a triangle.






