Pyramid together with a prism is a perfect polyhedron in three-dimensional space, their geometric characteristics are studied in high school. In this article, we will consider what pyramids are, what elements they consist of, and also briefly characterize the correct pyramids.
Geometric figure pyramid
From the point of view of geometry, the pyramid is a spatial figure, consisting of one polygon and several triangles. Getting this figure is quite simple. To do this, take a polygon with n sides, then choose an arbitrary point in space that will not lie in the plane of the polygon, and connect each vertex of the polygon to this point. Obviously, the figure thus formed will have n triangles connected to each other at one vertex.
To visualize the geometric shape of the described figure, let's take a picture.

This shows a quadrangular pyramid, the base of which isquadrilateral, and the side surface is formed by four triangles that have a common vertex.
Pyramid elements
Like any polyhedron, the pyramid is formed by three types of elements:
- edges;
- tops;
- ribs.
Faces are parts of planes that separate the internal volume of a figure from the surrounding space. If the base of the pyramid contains an n-gon, then the number of its faces is always n+1. Of these, n sides are triangular and one side is the mentioned n-gonal base.
Vertices are points where three or more faces of a figure intersect. The base region contains n vertices, each of which is formed by two triangular faces and a base. The point where n triangular sides meet is called the top of the pyramid. Thus, the figure under consideration consists of n+1 vertices.
Edges are straight lines that appear when two faces intersect. Each edge is bounded by two vertices at its ends. Any pyramid with an n-gon base contains 2n edges. Half of this number, that is, n, is formed solely by the intersection of side triangles.
Possible types of figures
The name of the figure under consideration is uniquely determined by the type of polygon at the base. For example, if it has three corners and three sides, then the pyramid will be triangular, if four - quadrangular, and so on.
Polygon can be convex and concave, as well as regular and general type. All this also determines the appearance of the pyramid.
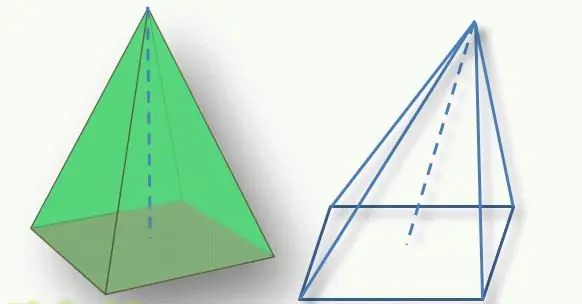
An important point in determining the type of figure is the position of the top of the pyramid relative to its base. The perpendicular segment drawn from the top to the polygonal base is called the height of the figure. If this segment intersects the base at its geometric center (for a triangle, this is the intersection of medians, for a quadrilateral, the intersection of diagonals), then the figure is called a straight line. Otherwise, they speak of an inclined pyramid.
If the n-gon of the base is regular (equilateral triangle, square, etc.), and the figure is straight, then it is called a regular pyramid.
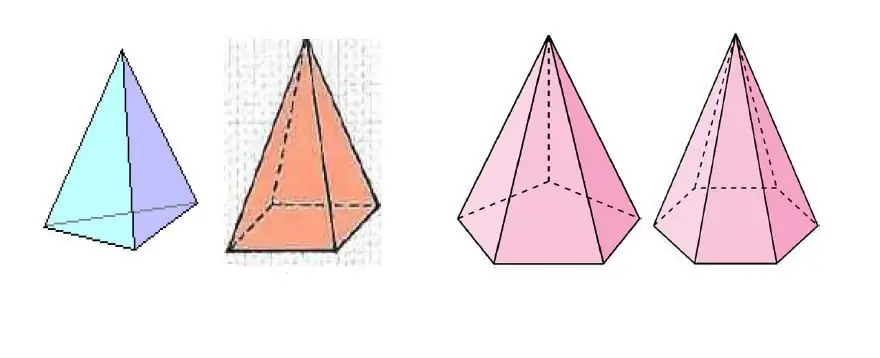
The picture above shows several pyramids, which differ in the number of sides of the polygon at the base.
Properties of regular pyramids
These pyramids differ from other figures of this class by a high degree of symmetry. In this regard, it is convenient to carry out various geometric calculations with them, for example, volume or surface area.
A regular pyramid contains an n-gon at the base, the area of which is uniquely determined from the knowledge of the length of its side. The lateral surface of the figure is formed by n identical triangles, which are equilateral. The edges of a regular pyramid located on the lateral surface are equal to each other. The value of the length of this edge is often used when calculating the apothem of a figure and determining the surface area.
The height of a regular pyramid is the second important characteristic of the figure (the first is the length of the edgegrounds). Height is used when calculating volume.
Any plane parallel to the base, which intersects the side faces of the pyramid, leads to the formation of a polygonal section. It is homothetic with respect to the base polygon. The described slice operation leads to the formation of a whole class of new figures - truncated regular pyramids.
The most famous pyramids

Of course, these are the regular quadrangular pyramids of the Egyptian pharaohs. In a place called Giza, there are more than 100 of these stone monuments, the perfection of design and the accuracy of the geometric parameters of which continue to amaze scientists to this day. The largest of them is the Pyramid of Cheops, which is about 146 meters high and about 230 meters long.
What exactly these pyramids served for, as well as by what mechanisms and when they were built, no one knows to this day.






