Kinematics is a part of physics that considers the laws of motion of bodies. Its difference from dynamics is that it does not consider the forces acting on a moving body. This article is devoted to the question of the kinematics of rotational motion.
Rotational motion and its difference from forward motion

If you pay attention to the surrounding moving objects, you can see that they either move in a straight line (the car is driving on the road, the plane is flying in the sky), or in a circle (the same car entering the turn, the rotation of the wheel). More complex types of object movement can be reduced as a first approximation to a combination of the two types noted.
Progressive movement involves changing the spatial coordinates of the body. In this case, it is often considered as a material point (geometric dimensions are not taken into account).
Rotational movement is a type of movement in whichthe system moves in a circle around some axis. Moreover, the object in this case is rarely considered as a material point, most often another approximation is used - an absolutely rigid body. The latter means that the elastic forces acting between the atoms of the body are neglected and it is assumed that the geometric dimensions of the system do not change during rotation. The simplest case is a fixed axle.
Kinematics of translational and rotational motion obeys the same laws of Newton. Similar physical quantities are used to describe both types of movement.
What quantities describe motion in physics?

Kinematics of rotational and translational motion uses three basic quantities:
- The path travelled. We will denote it by the letter L for translational and θ - for rotational motion.
- Speed. For a linear case, it is usually written with the Latin letter v, for movement along a circular path - with the Greek letter ω.
- Acceleration. For a linear and circular path, the symbols a and α are used, respectively.
The concept of a trajectory is also often used. But for the types of movement of objects under consideration, this concept becomes trivial, since the translational movement is characterized by a linear trajectory, and rotational - by a circle.
Linear and angular speeds
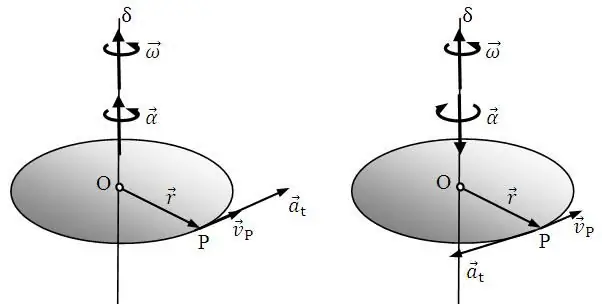
Let's start the kinematics of the rotational motion of a material pointviewed from the concept of speed. It is known that for the translational movement of bodies, this value describes which path will be overcome per unit of time, that is:
v=L / t
V is measured in meters per second. For rotation, it is inconvenient to consider this linear speed, since it depends on the distance to the axis of rotation. A slightly different characteristic is introduced:
ω=θ / t
This is one of the main formulas of the kinematics of rotational motion. It shows at what angle θ the whole system will turn around a fixed axis in time t.
Both of the above formulas reflect the same physical process of moving speed. Only for the linear case, the distance is important, and for the circular case, the angle of rotation.
Both formulas interact with each other. Let's get this connection. If we express θ in radians, then a material point rotating at a distance R from the axis, having made one revolution, will travel the path L=2piR. The expression for the linear velocity will take the form:
v=L / t=2piR / t
But the ratio of 2pi radians to time t is nothing but angular velocity. Then we get:
v=ωR
From here it can be seen that the greater the linear velocity v and the smaller the radius of rotation R, the greater the angular velocity ω.
Linear and angular acceleration
Another important characteristic in the kinematics of the rotational motion of a material point is the angular acceleration. Before we get to know him, let'sformula for a similar linear value:
1) a=dv / dt
2) a=Δv / Δt
The first expression reflects the instantaneous acceleration (dt ->0), while the second formula is appropriate if the speed changes uniformly over time Δt. The acceleration obtained in the second variant is called average.
Given the similarity of quantities that describe linear and rotational motion, for angular acceleration we can write:
1) α=dω / dt
2) α=Δω / Δt
The interpretation of these formulas is exactly the same as for the linear case. The only difference is that a shows how many meters per second the speed changes per unit of time, and α shows how many radians per second the angular speed changes over the same period of time.
Let's find the connection between these accelerations. Substituting the value for v, expressed in terms of ω, into either of the two equalities for α, we get:
α=Δω / Δt=Δv / Δt1 / R=a / R
It follows that the smaller the radius of rotation and the greater the linear acceleration, the greater the value of α.
Distance traveled and angle of turn
It remains to give formulas for the last of the three basic quantities in the kinematics of rotational motion around a fixed axis - for the angle of rotation. As in the previous paragraphs, we first write down the formula for uniformly accelerated rectilinear movement, we have:
L=v0 t + a t2 / 2
Full analogy with rotational movement leads to the following formula for it:
θ=ω0 t + αt2 / 2
The last expression allows you to get the rotation angle for any time t. Note that the circumference is 2pi radians (≈ 6.3 radians). If, as a result of solving the problem, the value of θ is greater than the specified value, then the body has made more than one revolution around the axis.
The formula for the relationship between L and θ is obtained by substituting the corresponding values for ω0and α through linear characteristics:
θ=v0 t / R + at2 / (2R)=L /R
The resulting expression reflects the meaning of the angle θ itself in radians. If θ=1 rad, then L=R, that is, an angle of one radian rests on an arc of length one radius.
Example of problem solving
Let's solve the following problem of rotational kinematics: we know that the car is moving at a speed of 70 km/h. Knowing that the diameter of its wheel is D=0.4 meters, it is necessary to determine the value of ω for it, as well as the number of revolutions that it will make when the car travels a distance of 1 kilometer.

To find the angular velocity, it is enough to substitute the known data into the formula for relating it to the linear velocity, we get:
ω=v / R=7104 / 3600 / 0, 2=97, 222 rad/s.
Similarly for the angle θ to which the wheel will turn after passing1 km, we get:
θ=L / R=1000 / 0, 2=5000 rad.
Given that one revolution is 6.2832 radians, we get the number of revolutions of the wheel that corresponds to this angle:
n=θ / 6, 2832=5000 / 6, 2832=795, 77 turns.
We answered the questions using the formulas in the article. It was also possible to solve the problem in a different way: calculate the time for which the car will travel 1 km, and substitute it into the formula for the angle of rotation, from which we can obtain the angular velocity ω. Answer found.






