The use of simple mechanisms in physics allows you to study various natural processes and laws. One of these mechanisms is the Atwood machine. Let's consider in the article what it is, what it is used for, and what formulas describe the principle of its operation.
What is Atwood's machine?
The named machine is a simple mechanism consisting of two weights, which are connected by a thread (rope) thrown over a fixed block. There are several points to be made in this definition. First, the masses of the loads are generally different, which ensures that they have acceleration under the action of gravity. Secondly, the thread connecting the loads is considered to be weightless and inextensible. These assumptions greatly facilitate subsequent calculations of the equations of motion. Finally, thirdly, the immovable block through which the thread is thrown is also considered to be weightless. In addition, during its rotation, the friction force is neglected. The schematic diagram below shows this machine.

Atwood's machine was inventedEnglish physicist George Atwood at the end of the 18th century. It serves to study the laws of translational motion, accurately determine the acceleration of free fall and experimentally verify Newton's second law.
Dynamics equations
Every schoolchild knows that bodies accelerate only if they are acted upon by external forces. This fact was established by Isaac Newton in the 17th century. The scientist put it in the following mathematical form:
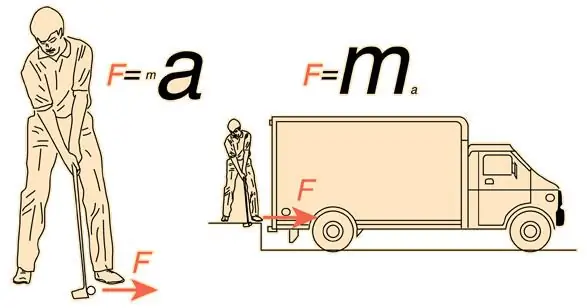
F=ma.
Where m is the inertial mass of the body, a is the acceleration.
Studying the laws of translational motion on the Atwood machine requires knowledge of the corresponding equations of dynamics for it. Suppose that the masses of two weights are m1and m2, where m1>m 2. In this case, the first weight will move down under the force of gravity, and the second weight will move up under the tension of the thread.
Let's consider what forces act on the first load. There are two of them: gravity F1 and thread tension force T. The forces are directed in different directions. Taking into account the sign of acceleration a, with which the load moves, we obtain the following equation of motion for it:
F1- T=m1a.
As for the second load, it is affected by forces of the same nature as the first. Since the second load moves with an upward acceleration a, the dynamics equation for it takes the form:
T - F2=m2a.
Thus, we have written two equations that contain two unknown quantities (a and T). This means that the system has a unique solution, which will be obtained later in the article.

Calculation of equations of dynamics for uniformly accelerated motion
As we have seen from the above equations, the resultant force acting on each load remains unchanged during the entire movement. The mass of each load also does not change. This means that the acceleration a will be constant. Such movement is called uniformly accelerated.
The study of uniformly accelerated motion on the Atwood machine is to determine this acceleration. Let's write down the system of dynamic equations again:
F1- T=m1a;
T - F2=m2a.
To express the value of the acceleration a, we add both equalities, we get:
F1- F2=a(m1+ m 2)=>
a=(F1 - F2)/(m1 + m 2).
Substituting the explicit value of gravity for each load, we get the final formula for determining the acceleration:
a=g(m1- m2)/(m1 + m2).
The ratio of the mass difference to their sum is called Atwood's number. Denote it na, then we get:
a=nag.
Checking the solution of dynamics equations

Above we defined the formula for the acceleration of the carAtwood. It is valid only if Newton's law itself is valid. You can check this fact in practice if you carry out laboratory work to measure some quantities.
Lab work with Atwood's machine is quite simple. Its essence is as follows: as soon as the loads that are at the same level from the surface are released, it is necessary to detect the time of movement of the goods with a stopwatch, and then measure the distance that any of the loads has moved. Assume that the corresponding time and distance are t and h. Then you can write down the kinematic equation of uniformly accelerated motion:
h=at2/2.
Where acceleration is uniquely determined:
a=2h/t2.
Note that in order to increase the accuracy of determining the value of a, several experiments should be carried out to measure hi and ti, where i is measurement number. After calculating the values ai, you should calculate the average value acpfrom the expression:
acp=∑i=1mai /m.
Where m is the number of measurements.
Equivalent to this equality and the one obtained earlier, we arrive at the following expression:
acp=nag.
If this expression turns out to be true, then so will Newton's second law.
Gravity calculation
Above, we assumed that the value of the free fall acceleration g is known to us. However, using the Atwood machine, the determination of forcegravity is also possible. To do this, instead of the acceleration a from the equations of dynamics, the value g should be expressed, we have:
g=a/na.
To find g, you should know what the translational acceleration is. In the paragraph above, we have already shown how to find it experimentally from the kinematics equation. Substituting the formula for a into the equality for g, we have:
g=2h/(t2na).
Calculating the value of g, it is easy to determine the force of gravity. For example, for the first load, its value will be:
F1=2hm1/(t2n a).
Determining the thread tension
The force T of the thread tension is one of the unknown parameters of the system of dynamic equations. Let's write these equations again:
F1- T=m1a;
T - F2=m2a.
If we express a in each equality, and equate both expressions, then we get:
(F1- T)/m1 =(T - F2)/ m2=>
T=(m2F1+ m1F 2)/(m1 + m2).
Substituting the explicit values of the gravity forces of the loads, we arrive at the final formula for the thread tension force T:
T=2m1m2g/(m1 + m2).
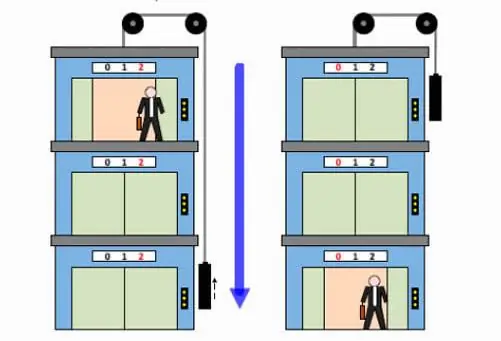
Atwood's machine has more than just theoretical utility. So, the lift (elevator) uses a counterweight in its work in order tolifting to the height of the payload. This design greatly facilitates the operation of the engine.






