What is Pearson's distribution law? The answer to this broad question cannot be simple and concise. The Pearson system was originally designed to model visible distorted observations. At the time, it was well known how to tune a theoretical model to match the first two cumulants or moments of observed data: any probability distribution can be directly expanded to form a group of location scales.
Pearson's hypothesis about the normal distribution of criteria
Except in pathological cases, the location scale can be made to match the observed mean (first cumulant) and variance (second cumulant) in an arbitrary manner. However, it was not known how to construct probability distributions in which skewness (standardized third cumulant) and kurtosis (standardized fourth cumulant) could be controlled equally freely. This need became apparent when trying to fit known theoretical models to observed data,who showed asymmetry.
In the video below you can see the analysis of Pearson's chi-distribution.

History
In his original work, Pearson identified four types of distributions (numbered I through IV) in addition to the normal distribution (which was originally known as type V). The classification depends on whether the distributions are supported over a limited interval, on a semi-axis, or on the entire real line, and whether they were potentially skewed or necessarily symmetrical.
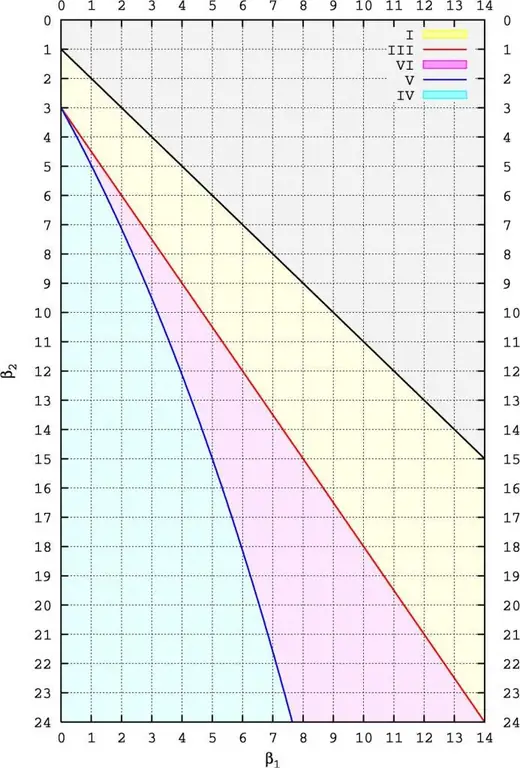
Two omissions were corrected in the second paper: he redefined the type V distribution (originally it was only the normal distribution, but now with inverse gamma) and introduced the type VI distribution. Together, the first two articles cover the five main types of the Pearson system (I, III, IV, V, and VI). In the third paper, Pearson (1916) introduced additional subtypes.

Improve the concept
Rind invented a simple way to visualize the parameter space of the Pearson system (or the distribution of criteria), which he later adopted. Today, many mathematicians and statisticians use this method. The types of Pearson distributions are characterized by two quantities, usually called β1 and β2. The first is the square of asymmetry. The second is the traditional kurtosis, or the fourth standardized moment: β2=γ2 + 3.
Modern mathematical methods define the kurtosis γ2 as cumulants instead of moments, so for a normaldistribution we have γ2=0 and β2=3. Here it is worth following the historical precedent and using β2. The diagram on the right shows which type a particular Pearson distribution is (denoted by the dot (β1, β2).
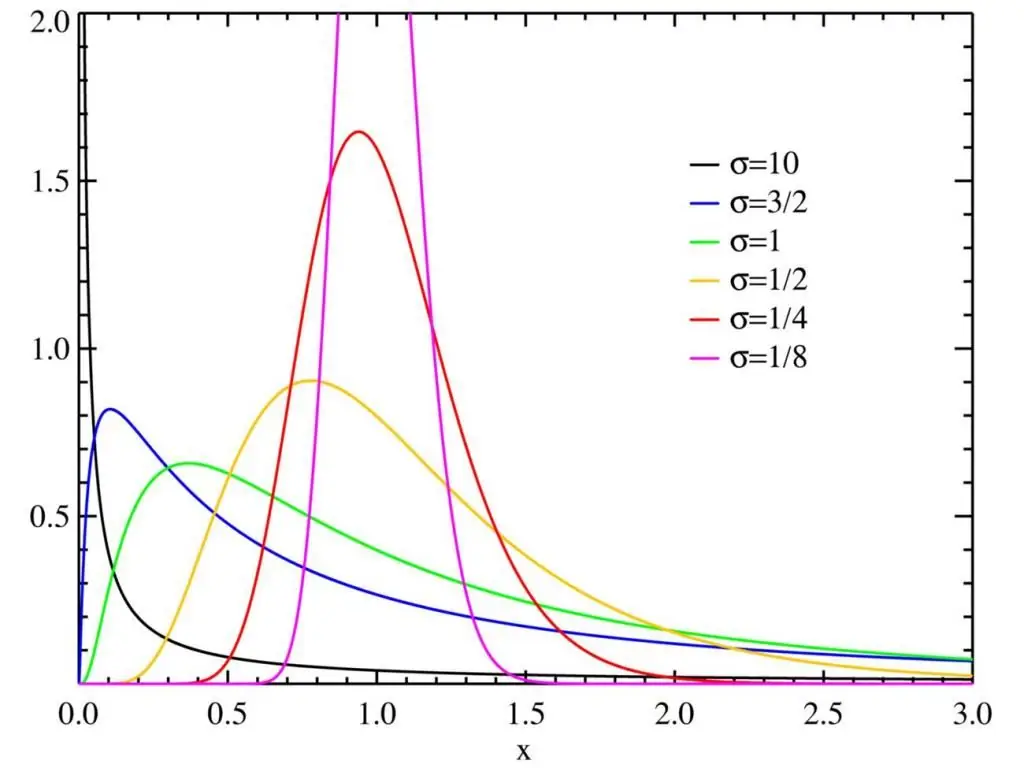
Many of the skewed and/or non-mesokurtic distributions we know today were not yet known in the early 1890s. What is now known as the beta distribution was used by Thomas Bayes as the posterior parameter of the Bernoulli distribution in his 1763 paper on inverse probability.
The beta distribution rose to prominence due to its presence in the Pearson system and was known until the 1940s as the Pearson type I distribution. The Type II distribution is a special case of Type I, but it's usually no longer singled out.
The Gamma distribution originated from his own work and was known as the Pearson Type III Normal Distribution before it acquired its modern name in the 1930s and 1940s. An 1895 paper by a scientist presented the Type IV distribution, which contains Student's t-distribution, as a special case, predating William Seely Gosset's subsequent use by several years. His 1901 paper presented a distribution with inverse gamma (type V) and beta primes (type VI).
Another opinion
According to Ord, Pearson developed the basic form of equation (1) based on the formula for the derivative of the logarithm of the normal distribution density function (which gives a linear division by the quadraticstructure). Many specialists are still engaged in testing the hypothesis about the distribution of the Pearson criteria. And it proves its effectiveness.
Who was Karl Pearson
Karl Pearson was an English mathematician and biostatistician. He is credited with creating the discipline of mathematical statistics. In 1911 he founded the world's first department of statistics at University College London and made significant contributions to the fields of biometrics and meteorology. Pearson was also a supporter of social Darwinism and eugenics. He was Sir Francis G alton's protégé and biographer.
Biometrics
Karl Pearson was instrumental in creating the school of biometrics, which was a competing theory for describing the evolution and inheritance of populations at the turn of the 20th century. His series of eighteen papers "Mathematical Contributions to the Theory of Evolution" established him as the founder of the biometric school of inheritance. In fact Pearson devoted much of his time during 1893-1904 to development of statistical methods for biometrics. These methods, which are widely used today for statistical analysis, include the chi-square test, standard deviation, correlation and regression coefficients.
The question of heredity
Pearson's law of heredity stated that the germ plasm consists of elements inherited from parents, as well as from more distant ancestors, the proportion of which varied according to various characteristics. Karl Pearson was a follower of G alton, and although theirworks differed in some respects, Pearson used a significant amount of his teacher's statistical concepts in formulating a biometric school for inheritance, such as the law of regression.
School Features
The biometric school, unlike the Mendelians, was not focused on providing a mechanism for inheritance, but on providing a mathematical description that was not causal in nature. While G alton proposed a discontinuous theory of evolution in which species would change in large leaps rather than small changes that accumulated over time, Pearson pointed out flaws in this argument and actually used his ideas to develop a continuous theory of evolution. The Mendelians preferred the discontinuous theory of evolution.
While G alton focused mainly on the application of statistical methods to the study of heredity, Pearson and his colleague Weldon expanded their reasoning in this area, variation, correlations of natural and sexual selection.
A look at evolution
For Pearson, the theory of evolution was not intended to identify the biological mechanism that explains the patterns of inheritance, while the Mendelian approach declared the gene to be the mechanism of inheritance.
Pearson criticized Bateson and other biologists for not adopting biometric methods in their study of evolution. He condemned scientists who did not focus onstatistical validity of their theories, stating:
"Before we can accept [any cause of progressive change] as a factor, we must not only show its plausibility, but, if possible, demonstrate its quantitative ability."
Biologists have succumbed to "almost metaphysical speculations about the causes of heredity" that have replaced the process of collecting experimental data, which may actually allow scientists to narrow down potential theories.
Laws of nature
For Pearson, the laws of nature were useful for making accurate predictions and for summarizing trends in observed data. The reason was the experience “that a certain sequence happened and repeated in the past.”
Thus, identifying a particular mechanism of genetics has not been a worthy endeavor for biologists, who should instead focus on mathematical descriptions of the empirical data. This partly led to a bitter dispute between biometrists and Mendelians, including Bateson.
After the latter rejected one of Pearson's manuscripts describing a new theory of progeny variation or homotypy, Pearson and Weldon founded the Biometrika company in 1902. Although the biometric approach to inheritance eventually lost its Mendelian perspective, the methods they developed at the time are vital to the study of biology and evolution today.






