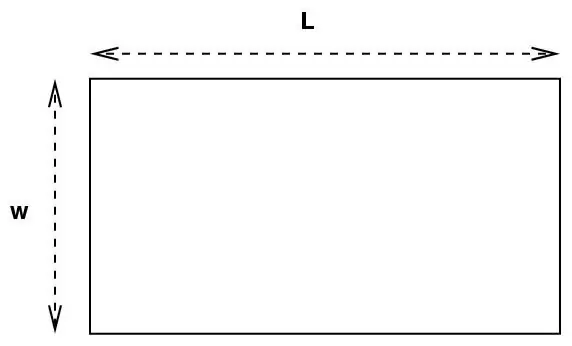
One of the first formulas learned in mathematics is how to calculate the area of a rectangle. It is also the most commonly used. Rectangular surfaces are all around us, so we often need to know their area. At least to find out if the available paint is enough to paint the floors.
What units of area are there?
If we talk about the one that is accepted as international, then it will be a square meter. It is convenient to use when calculating the areas of walls, ceilings or floors. They indicate the area of housing.
When it comes to smaller objects, then square decimeters, centimeters or millimeters are introduced. The latter are needed if the figure is no larger than a fingernail.
When measuring the area of a city or country, square kilometers are the most appropriate. But there are also units that are used to indicate the size of the area: ares and hectares. The first of them is also called a hundred.

What if the sides of the rectangle are given?
This is the easiest way to calculate the area of a rectangle. It is enough just to multiply both known values: length and width. The formula looks like this: S=ab. Here, the letters a and b denote the length and width.
Similarly, the area of a square, which is a special case of a rectangle, is calculated. Since all its sides are equal, the product becomes the square of the letter a.
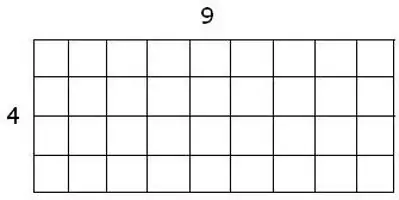
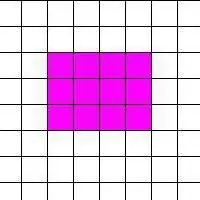
What if the figure is depicted on checkered paper?
In this situation, you need to rely on the number of cells inside the shape. By their number, it can be easy to calculate the area of \u200b\u200ba rectangle. But this can be done when the sides of the rectangle coincide with the cell lines.
Often there is such a position of the rectangle, in which its sides are inclined with respect to the paper line. Then it is difficult to determine the number of cells, so the calculation of the area of the rectangle becomes more complicated.
You first need to know the area of the rectangle, which can be drawn by cells exactly around the given one. It's simple: multiply height and width. Then subtract from the resulting value the area of all right-angled triangles. And there are four of them. By the way, they are calculated as half the product of the legs.
The final result will give the area of the given rectangle.
What to do if the sides are unknown, but its diagonal is givenand the angle between the diagonals?
Before finding the area of a rectangle, in this situation, you need to calculate its sides in order to use the already familiar formula. First you need to remember the property of its diagonals. They are equal and bisect the point of intersection. You can see in the drawing that the diagonals divide the rectangle into four isosceles triangles, which are equal in pairs to each other.
The equal sides of these triangles are defined as half of the diagonal, which is known. That is, in each triangle there are two sides and an angle between them, which are given in the problem. You can use the cosine theorem.
One side of the rectangle will be calculated using a formula that uses the equal sides of the triangle and the cosine of the given angle. To calculate the second value, the cosine will have to be taken from an angle equal to the difference of 180 and a known angle.
Now the problem of how to calculate the area of a rectangle comes down to a simple multiplication of the two obtained sides.
What to do if the perimeter is given in the problem?
Usually, the condition also indicates the ratio of length and width. The question of how to calculate the area of a rectangle, in this case, is easier with a specific example.
Assume that in the problem the perimeter of a certain rectangle is 40 cm. It is also known that its length is one and a half times greater than its width. You need to know its area.
The solution of the problem begins with writing the perimeter formula. It is more convenient to write it as the sum of the length and width, each of which is multiplied bytwo separately. This will be the first equation in the system to be solved.
The second is related to the aspect ratio known by condition. The first side, that is, the length, is equal to the product of the second (width) and the number 1, 5. This equality must be substituted into the formula for the perimeter.
It turns out that it is equal to the sum of two monomials. The first is the product of 2 and an unknown width, the second is the product of the numbers 2 and 1, 5 and the same width. In this equation, there is only one unknown - this is the width. You need to count it, and then use the second equality to calculate the length. All that remains is to multiply these two numbers to find out the area of the rectangle.
Calculations give the following values: width - 8 cm, length - 12 cm, and area - 96 cm2. The last number is the answer of the considered problem.






