If the linear movement of bodies is described in classical mechanics using Newton's laws, then the characteristics of the movement of mechanical systems along circular trajectories are calculated using a special expression, which is called the equation of moments. What moments are we talking about and what is the meaning of this equation? These and other questions are revealed in the article.
Moment of force
Everyone is well aware of the Newtonian force, which, acting on the body, leads to the imparting of acceleration to it. When such a force is applied to an object that is fixed on a certain axis of rotation, then this characteristic is usually called the moment of force. The moment of force equation can be written as follows:
M¯=L¯F¯
The picture explaining this expression is shown below.
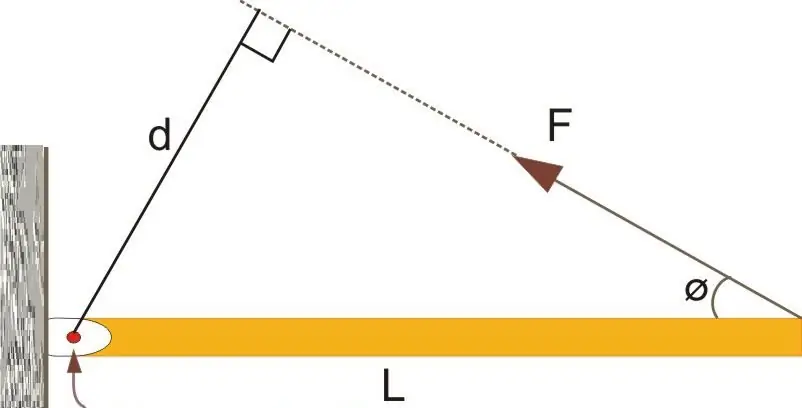
Here you can see that the force F¯ is directed to the vector L¯ at an angle Φ. The vector L¯ itself is assumed to be directed from the axis of rotation (indicated by the arrow) to the point of applicationF¯.
The formula above is a product of two vectors, so M¯ is also directional. Where will the moment of force M¯ be turned? This can be determined by the right hand rule (four fingers are directed along the trajectory from the end of the vector L¯ to the end of F¯, and the left thumb indicates the direction of M¯).
In the figure above, the expression for the moment of force in scalar form will take the form:
M=LFsin(Φ)
If you look closely at the figure, you can see that Lsin(Φ)=d, then we have the formula:
M=dF
The value of d is an important characteristic in calculating the moment of force, as it reflects the effectiveness of the applied F to the system. This value is called the lever of force.
The physical meaning of M lies in the ability of the force to rotate the system. Everyone can feel this ability if they open the door by the handle, pushing it near the hinges, or if they try to unscrew the nut with a short and long key.
Equilibrium of the system
The concept of moment of force is very useful when considering the equilibrium of a system that is acted upon by multiple forces and has an axis or point of rotation. In such cases, apply the formula:
∑iMi¯=0
That is, the system will be in equilibrium if the sum of all moments of forces applied to it is zero. Note that this formula contains the sign of the vector over the moment, that is, when solving, one should not forget to take into account the sign of thisquantities. The generally accepted rule is that the acting force that rotates the system counterclockwise creates a positive Mi¯.

A striking example of problems of this type are problems with the balance of Archimedes' levers.
Moment of momentum
This is another important characteristic of circular motion. In physics, it is described as the product of the momentum and the lever. The momentum equation looks like this:
T¯=r¯p¯
Here p¯ is the momentum vector, r¯ is the vector connecting the rotating material point with the axis.
The figure below illustrates this expression.
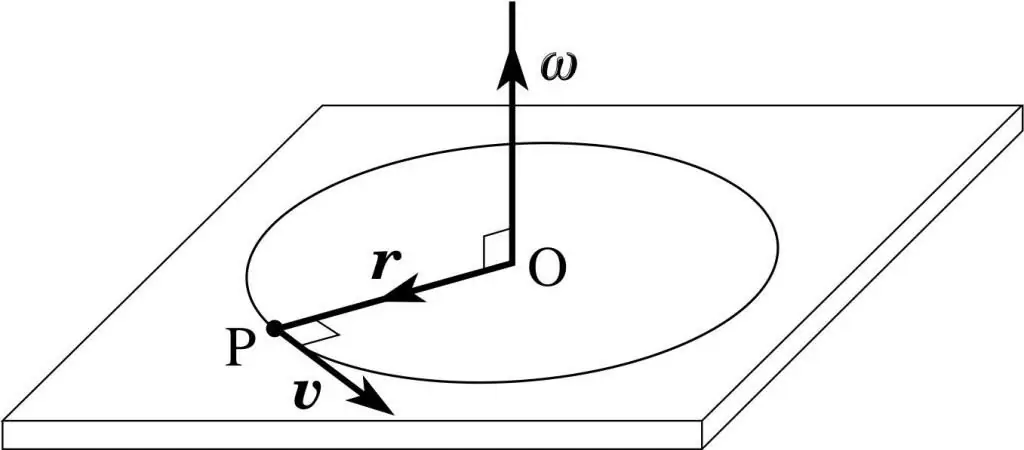
Here ω is the angular velocity, which will appear further in the moment equation. Note that the direction of the vector T¯ is found by the same rule as M¯. In the figure above, T¯ in direction will coincide with the angular velocity vector ω¯.
The physical meaning of T¯ is the same as the characteristics of p¯ in the case of linear motion, i.e. angular momentum describes the amount of rotational motion (stored kinetic energy).
Moment of inertia
The third important characteristic, without which it is impossible to formulate the equation of motion of a rotating object, is the moment of inertia. It appears in physics as a result of mathematical transformations of the formula for the angular momentum of a material point. Let's show you how it's done.
Let's imagine the valueT¯ as follows:
T¯=r¯mv¯, where p¯=mv¯
Using the relationship between angular and linear velocities, we can rewrite this expression as follows:
T¯=r¯mr¯ω¯, where v¯=r¯ω¯
Write the last expression as follows:
T¯=r2mω¯
The value r2m is the moment of inertia I for a point of mass m that makes a circular motion around an axis at a distance r from it. This special case allows us to introduce the general equation of the moment of inertia for a body of arbitrary shape:
I=∫m (r2dm)
I is an additive quantity, the meaning of which lies in the inertia of the rotating system. The larger I, the more difficult it is to spin the body, and it takes considerable effort to stop it.

Moment equation
We have considered three quantities, the name of which begins with the word "moment". This was done intentionally, since they are all connected in one expression, called the 3-moment equation. Let's get it out.
Consider the expression for the angular momentum T¯:
T¯=Iω¯
Find how the value of T¯ changes in time, we have:
dT¯/dt=Idω¯/dt
Given that the derivative of the angular velocity is equal to that of the linear velocity divided by r, and expanding the value of I, we arrive at the expression:
dT¯/dt=mr21/rdv¯/dt=rma¯, where a¯=dv¯/dt is linear acceleration.
Note that the product of mass and acceleration is nothing but the acting external force F¯. As a result, we get:
dT¯/dt=rF¯=M¯
We came to an interesting conclusion: the change in the angular momentum is equal to the moment of the acting external force. This expression is usually written in a slightly different form:
M¯=Iα¯, where α¯=dω¯/dt - angular acceleration.
This equality is called the equation of moments. It allows you to calculate any characteristic of a rotating body, knowing the parameters of the system and the magnitude of the external impact on it.
Conservation law T¯
The conclusion obtained in the previous paragraph indicates that if the external moment of forces is equal to zero, then the angular momentum will not change. In this case, we write the expression:
T¯=const. or I1ω1¯=I2ω2 ¯
This formula is called the law of conservation of T¯. That is, any changes within the system do not change the total angular momentum.
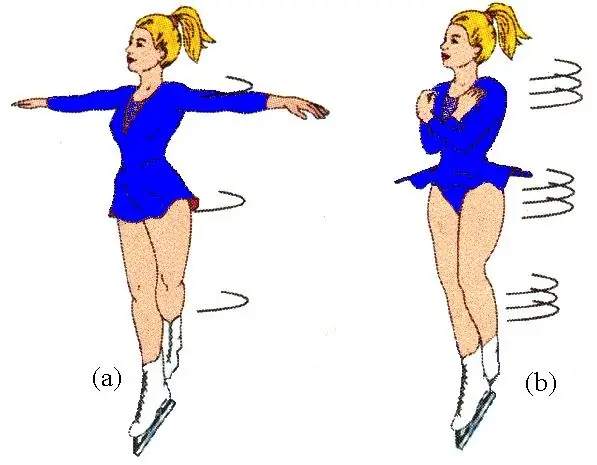
This fact is used by figure skaters and ballerinas during their performances. It is also used if it is necessary to rotate an artificial satellite moving in space around its axis.






