Specific Impulse (SP) is a measure of how efficiently a rocket or engine uses fuel. By definition, this is the total surge delivered per unit of power consumed, and is equivalent in size to the thrust generated divided by the mass flow. If kilograms are used as the unit of propellant, then specific impulse is measured in terms of velocity. If a weight in newtons or pounds-force is used instead, then the specific value is expressed in terms of time, most commonly in seconds.
Multiplying the flow velocity by the standard gravity converts the GI to mass.
Tsiolkovsky equation
The specific impulse of a higher mass engine is more efficiently used to generate forward thrust. And in the case when a rocket is used, less fuel is required. It is he who is needed for this delta-v. According to the equationTsiolkovsky, in the specific impulse of a rocket engine, the motor is more efficient in climbing, distance and speed. This performance is less important in reactive models. Which use wings and outside air for combustion. And carry a payload that is much heavier than fuel.
Specific impulse includes motion generated by outside air used for combustion and depleted by spent fuel. Jet engines use the outside atmosphere for this. And therefore they have a much higher UI than rocket engines. This concept, from the point of view of the consumed mass of fuel, has units of measurement of distance over time. Which are an artificial value called "effective exhaust gas velocity". This is higher than the actual exhaust velocity. Because the mass of air for combustion is not taken into account. Actual and effective exhaust velocity are the same in rocket engines that do not use air or, for example, water.
General considerations
The amount of fuel is usually measured in units of mass. If it is used, then the specific impulse is the impulse per EM, which, as shown by the size analysis, has units of velocity. And so UI is often measured in meters per second. And often referred to as the effective speed of the exhaust. However, if mass is used, the specific impulse of the fuel divided by the force turns out to be a unit of time. And so specific pushes are measured in seconds.
It is this rule that is the main one in the modern world, widely used withcoefficient r0 (constant of gravitational acceleration on the Earth's surface).
It is worth noting that the rate of change of the rocket's impulse (including its fuel) per unit of time is equal to the specific thrust impulse.
Specifics
The higher the push, the less fuel is required to generate a given thrust for a certain amount of time. In this regard, the liquid is more effective, the greater its UI. However, this should not be confused with energy efficiency, which can decrease with increasing thrust, since the specific impulse of the engine, which gives high results, requires a lot of energy to do this.
Also, it is important to distinguish and not confuse a pull with a specific push. UI is created per unit of fuel consumed. And thrust is the instantaneous or peak force that is generated by a particular device. In many cases, very high specific impulse propulsion systems - some ion installations reach 10,000 seconds - produce low thrust.
When calculating the push, only the fuel that is carried with the vehicle before use is taken into account. Therefore, for a rocket chemist, the mass will include both the propellant and the oxidizer. For air-breathed engines, only the amount of liquid is taken into account, not the mass of air passing through the engine.
Atmospheric drag and the plant's inability to maintain high specific impulse at high burn rates is precisely the reason why all the fuel is not being used as quickly as possible.
Heaviera motor with good MI may not be as effective in climbing, distance or speed as a light instrument with poor performance
If it wasn't for air resistance and reduced fuel consumption during flight, MI would be a direct measure of an engine's efficiency in converting mass into forward propulsion.
Specific impulse in seconds
The most common unit for a particular push is Hs. Both in the context of the SI and in cases where imperial or conventional values are used. The advantage of seconds is that the unit and numeric value are the same for all systems and are essentially universal. Almost all manufacturers list their engine performance in seconds. And such a device is also useful for determining the specifics of an aircraft device.
Using meters per second to find the effective exhaust velocity is also fairly common. This block is intuitive when describing rocket engines, although the effective exhaust velocity of the devices may differ significantly from the actual one. This is most likely due to the fuel and oxidizer being dumped overboard after the turbopumps are turned on. For air-breathing jet engines, the effective exhaust velocity has no physical meaning. Although it may be used for comparison purposes.
Units
Values expressed in Ns (in kilograms) are not uncommon and numerically equal to the effective exhaust velocity in m / s (from Newton's second law and hisdefinitions).
Another equivalent unit is specific fuel consumption. It has units of measure such as g (kN s) or lb/hr. Any of these units is inversely proportional to specific impulse. And fuel consumption is widely used to describe the performance of jet engines.
General definition
For all vehicles, the specific impulse (push per unit weight of fuel on Earth) in seconds can be determined by the following equation.
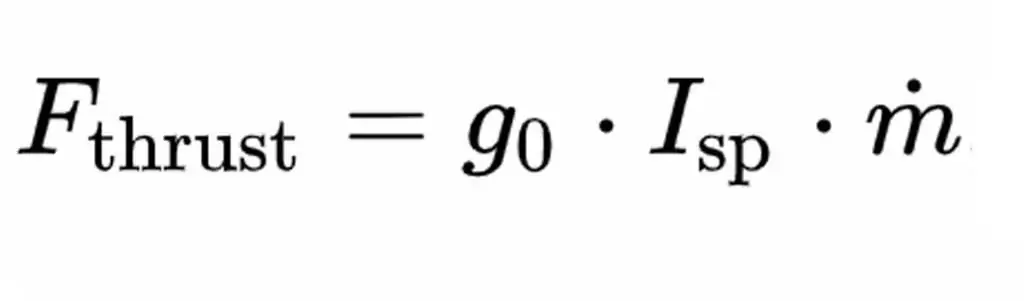
To clarify the situation, it is important to clarify that:
- F is the standard force of gravity, which is nominally stated as the power on the Earth's surface, in m/s2 (or ft/s squared).
- g is the mass flow rate in kg/s, which appears negative with respect to the rate of change of the vehicle's mass over time (as fuel is pushed out).
Measurement
The English unit, the pound, is more commonly used than other units. And also when applying this value per second for the flow rate, when converting, the constant r 0 becomes unnecessary. As it becomes dimensionally equivalent to pounds divided by g 0.
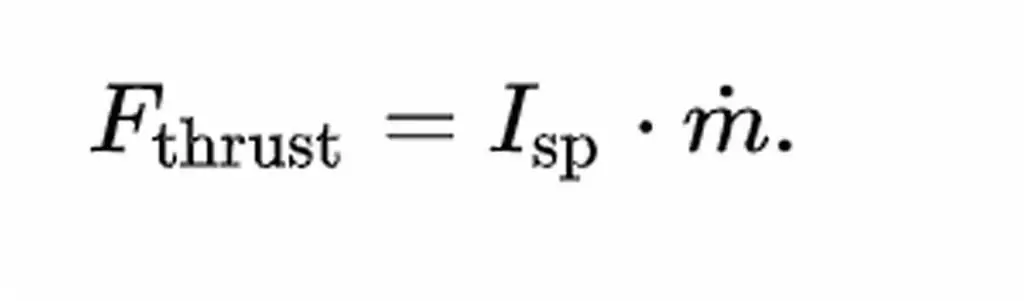
I sp in seconds is the time for which the device can generate a specific impulse of thrust of a rocket engine, given an amount of propellant whose weight is equal to thrust.
The advantage of this wording is that it can be used torockets, where the entire reaction mass is transported on board, as well as for aircraft, where most of the reaction mass is taken from the atmosphere. Also, it gives a result that is independent of the units used.
Specific impulse as velocity (effective exhaust velocity)
Because of the geocentric factor g 0 in the equation, many prefer to define rocket thrust (in particular) in terms of thrust per unit mass of fuel flow. This is an equally valid (and in some ways somewhat simpler) way to determine the specific impulse efficiency of a propellant. If we consider other options, the situation will be almost everywhere the same. Rockets of a certain specific impulse are simply the effective exhaust velocity relative to the device. The two attributes of a particular push are proportional to each other and are related as follows.
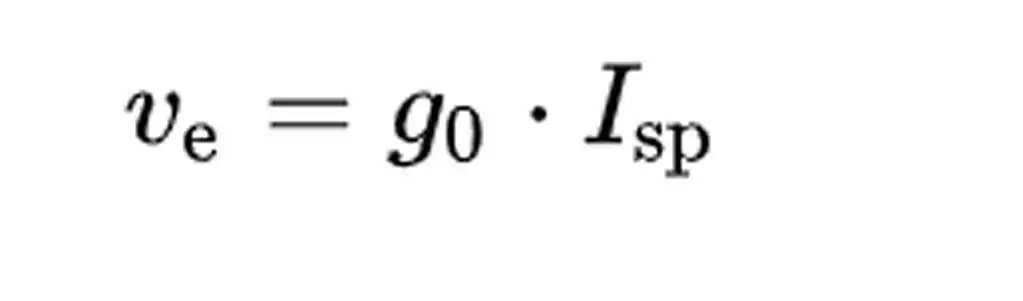
To use the formula, you need to understand that:
- I - specific impulse in seconds.
- v - push, measured in m/s. Which is equal to the effective exhaust velocity measured in m/s (or ft/s, depending on the value of g).
- g is the standard of gravity, 9.80665 m/s 2. In Imperial units 32.174 ft/s 2.
This equation also applies to jet engines, but is rarely used in practice.
Note that sometimes different characters are used. For example, c is also considered for exhaust velocity. While the symbolsp can logically be used for UI in units of N s/kg. To avoid confusion, it is desirable to reserve it for a specific value, measured in seconds before the start of the description.
This is related to the thrust or the force of movement of the specific impulse of the rocket engine, the formula.
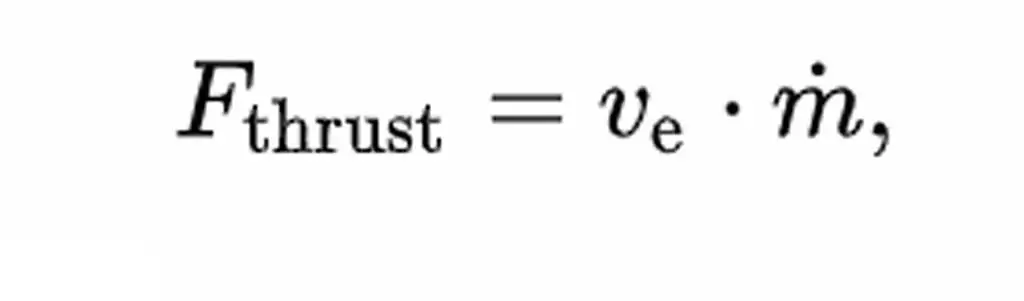
Here m is the mass fuel consumption, which is the rate of decrease in the magnitude of the vehicle.
Minimization
The rocket must carry all of its propellant. Therefore, the mass of unburned food must be accelerated along with the device itself. Minimizing the amount of fuel needed to achieve a given thrust is critical to building efficient rockets.
Tsiolkovsky's specific impulse formula shows that for a rocket with a given empty mass and a certain amount of fuel, the total change in velocity can be achieved in proportion to the effective speed of the exhaust.
A spacecraft without a propeller moves in an orbit determined by its trajectory and any gravitational field. Deviations from the corresponding velocity pattern (called Δv) are achieved by pushing the exhaust gas mass in the opposite direction of the desired change.
Actual speed versus effective speed

Here it is worth noting that these two concepts can differ significantly. For example, when a rocket is launched in the atmosphere, the air pressure outside the engine causesbraking force. Which reduces the specific impulse and the effective exhaust velocity is reduced, while the actual swiftness remains practically unchanged. In addition, sometimes rocket engines have a separate nozzle for turbine gas. The calculation of the effective exhaust velocity then requires averaging the two mass flows as well as taking into account any atmospheric pressure.
Increase efficiency
For air-breathed jet engines, in particular turbofans, the actual exhaust speed and effective speed differ by several orders of magnitude. This is due to the fact that when using air as the reaction mass, a significant additional momentum is achieved. This allows for a better match between airspeed and exhaust velocity, which saves energy and fuel. And significantly increases the effective component while reducing the actual swiftness.
Energy Efficiency
For rockets and rocket-like engines such as ion models, sp implies lower energy efficiency.
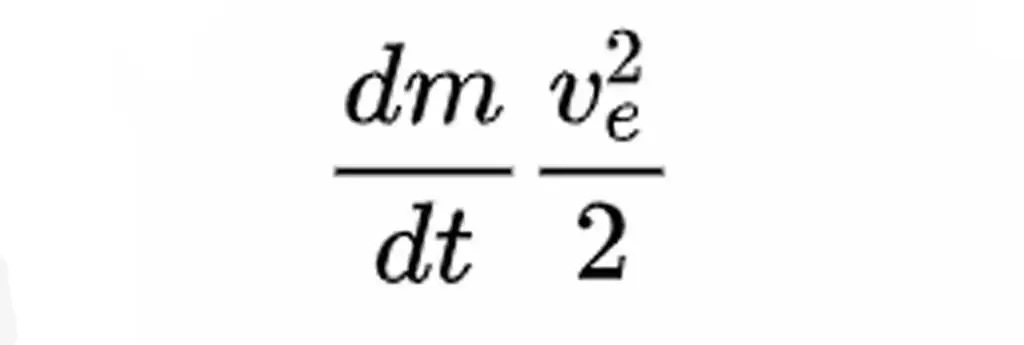
In this formula, v e is the actual jet velocity.
Hence the required force is proportional to each exhaust velocity. At higher speeds, much more power is required for the same thrust, resulting in less energy efficiency by one unit.
However, the total energy for a mission depends on the total fuel usage as well as how much energy is required per unit. For low exhaust speedregarding the delta-v mission, huge amounts of reaction mass are needed. In fact, for this reason, a very low exhaust velocity is not energy efficient. But it turns out that no type has the highest scores.
Variable
Theoretically, for a given delta-v, in space, among all fixed exhaust velocity values, ve=0.6275 is the most energy efficient for a given final mass. To learn more, you can view the energy in the propulsion apparatus of the spacecraft.
However, variable exhaust rates can be even more energy efficient. For example, if a rocket is accelerated at some positive initial velocity using an exhaust velocity that is equal to the product velocity, no energy is lost as a kinetic component of the reaction mass. As it becomes stationary.






