In the early 20th century, a young scientist named Albert Einstein looked at the properties of light and mass and how they relate to each other. The result of his reflections was the theory of relativity. His work changed modern physics and astronomy in a way that is still felt today. Each student studies their famous E=MC2 equation to understand how mass and energy are related. This is one of the fundamental facts of the existence of the cosmos.
What is the cosmological constant?
As deep as Einstein's equations for general relativity were, they presented a problem. He sought to explain how mass and light exist in the universe, how their interaction can lead to a static (that is, not expanding) universe. Unfortunately, his equations predicted that it would either contract or expand, and would continue to do so forever, but would eventually reach a point where it would contract.
It didn't feel right to him, so Einstein had to explain a way to hold gravity,to explain the static universe. After all, most physicists and astronomers of his time simply assumed that this was the case. So Einstein invented the Fudge factor, called the "cosmological constant," which gave order to the equations and resulted in a universe that neither expands nor contracts. He came up with the sign "lambda" (Greek letter), denoting the energy density in the vacuum of space. It controls the expansion, and its lack stops this process. Now a factor was needed to explain the cosmological theory.
How to calculate?

Albert Einstein presented the first version of the general theory of relativity (GR) to the public on November 25, 1915. Einstein's original equations looked like this:
In the modern world, the cosmological constant is:
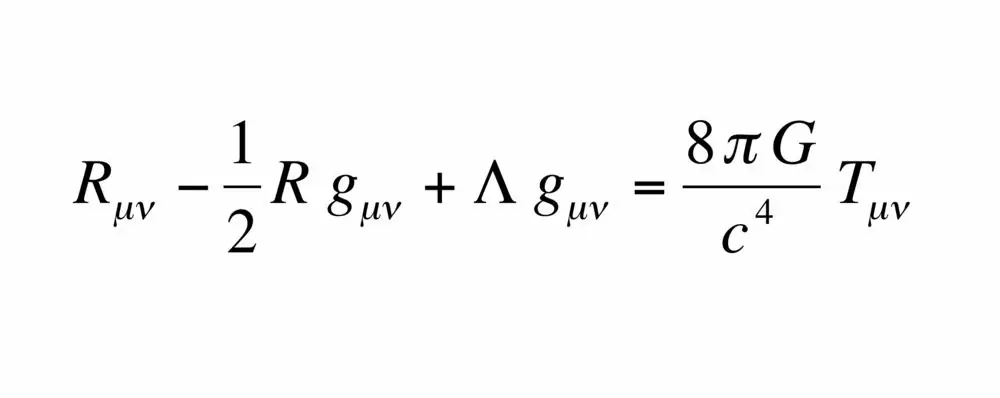
This equation describes the theory of relativity. Also, a constant is also called a lambda member.
Galaxies and the expanding universe
The cosmological constant didn't fix things the way he expected. Actually, it worked, but only for a while. The problem of the cosmological constant has not been solved.

This continued until another young scientist, Edwin Hubble, made a deep observation of variable stars in distant galaxies. Their flicker revealed the distances to these cosmic structures and more.
Hubble's work has demonstratednot only that the universe included many other galaxies, but as it turned out, it was expanding, and now we know that the rate of this process changes over time. This largely reduced Einstein's cosmological constant to zero, and the great scientist had to revise his assumptions. Researchers have not abandoned it completely. However, Einstein later called adding his constant to general relativity the biggest mistake of his life. But is it?
New cosmological constant
In 1998, a team of scientists working with the Hubble Space Telescope, studying distant supernovae, noticed something completely unexpected: the expansion of the universe is accelerating. Moreover, the pace of the process is not what they expected and has been in the past.
Given that the universe is filled with mass, it seems logical that the expansion should slow down, even if it were so small. Thus, this discovery seemed to contradict what the equations and Einstein's cosmological constant predicted. Astronomers did not understand how to explain the apparent acceleration of expansion. Why, how is this happening?
Answers to questions
To explain the acceleration and the cosmological notions about it, scientists have returned to the idea of the original theory.
Their latest speculation does not rule out the existence of something called dark energy. It is something that cannot be seen or felt, but its effects can be measured. It's the same as darkmatter: its effect can be determined by how it affects light and visible matter.
Astronomers may not yet know what this dark energy is. However, they know that it affects the expansion of the universe. To understand these processes, more time is needed for observation and analysis. Maybe the cosmological theory isn't such a bad idea after all? After all, it can be explained by assuming that dark energy does exist. Apparently, this is true and scientists need to look for further explanations.
What happened at the beginning?
Einstein's original cosmological model was a static homogeneous model with a spherical geometry. The gravitational effect of matter caused an acceleration in this structure, which Einstein could not explain, since at that time it was not known that the universe was expanding. Therefore, the scientist introduced the cosmological constant into his equations of general relativity. This constant is applied to counteract the gravitational pull of matter, and so it has been described as the anti-gravity effect.
Omega Lambda
Instead of the cosmological constant itself, researchers often refer to the relationship between the energy density due to it and the critical density of the universe. This value is usually denoted as follows: ΩΛ. In a flat universe, ΩΛ corresponds to a fraction of its energy density, which is also explained by the cosmological constant.
Note that this definition is related to the critical density of the current epoch. It changes over time, but the densityenergy, due to the cosmological constant, remains unchanged throughout the history of the universe.
Let's consider further how modern scientists develop this theory.
Cosmological proof
The current study of the accelerating universe is now very active, with many different experiments covering vastly different time scales, length scales and physical processes. A cosmological CDM model has been created, in which the Universe is flat and has the following characteristics:
- energy density, which is about 4% of baryonic matter;
- 23% dark matter;
- 73% of the cosmological constant.
The critical observational result that brought the cosmological constant to its current significance was the discovery that distant Type Ia (0<z<1) supernovae used as standard candles were weaker than expected in a slowing universe. Since then, many groups have confirmed this result with more supernovae and a wider range of redshifts.

Let's explain in more detail. Of particular importance in current cosmological thinking are the observations that extremely high redshift (z>1) supernovae are brighter than expected, which is a signature that is expected from the deceleration time leading up to our current acceleration period. Prior to the release of supernova results in 1998, there were already several lines of evidence that paved the way for relatively rapidacceptance of the theory of acceleration of the Universe with the help of supernovae. In particular, three of them:
- The universe turned out to be younger than the oldest stars. Their evolution has been well studied, and observations of them in globular clusters and elsewhere show that the oldest formations are over 13 billion years old. We can compare this to the age of the universe by measuring its expansion rate today and tracing back to the time of the Big Bang. If the universe slowed down to its current speed, then the age would be less than if it accelerated to its current rate. A flat, matter-only universe would be about 9 billion years old, a major problem considering it is several billion years younger than the oldest stars. On the other hand, a flat universe with 74% of the cosmological constant would be about 13.7 billion years old. So seeing that she is currently accelerating solved the age paradox.
- Too many distant galaxies. Their number has already been widely used in attempts to estimate the deceleration of the expansion of the Universe. The amount of space between two redshifts differs depending on the expansion history (for a given solid angle). Using the number of galaxies between two redshifts as a measure of the volume of space, observers have determined that distant objects appear too large compared to predictions of a slowing universe. Either the luminosity of galaxies or their number per unit volume evolved over time in unexpected ways, or the volumes we calculated were wrong. The accelerating matter couldwould explain the observations without triggering any strange theory of galaxy evolution.
- The observable flatness of the universe (despite incomplete evidence). Using measurements of temperature fluctuations in the cosmic microwave background (CMB), since the time when the universe was about 380,000 years old, it can be concluded that it is spatially flat to within a few percent. By combining these data with an accurate measurement of the density of matter in the universe, it becomes clear that it has only about 23% of the critical density. One way to explain the missing energy density is to apply the cosmological constant. As it turned out, a certain amount of it is simply necessary to explain the acceleration observed in the supernova data. This was just the factor needed to make the universe flat. Therefore, the cosmological constant resolved the apparent contradiction between observations of matter density and CMB.
What is the point?
To answer the questions that arise, consider the following. Let's try to explain the physical meaning of the cosmological constant.
We take the GR equation-1917 and put the metric tensor gab out of brackets. Therefore, inside the brackets we will have the expression (R / 2 - Λ). The value of R is represented without indices - this is the usual, scalar curvature. If you explain on the fingers - this is the reciprocal of the radius of the circle / sphere. Flat space corresponds to R=0.
In this interpretation, a non-zero value of Λ means that our Universe is curvedby itself, including in the absence of any gravity. However, most physicists do not believe this and believe that the observed curvature must have some internal cause.
Dark matter

This term is used for hypothetical matter in the universe. It is designed to explain a lot of problems with the standard Big Bang cosmological model. Astronomers estimate that about 25% of the universe is made up of dark matter (perhaps assembled from nonstandard particles such as neutrinos, axions, or Weakly Interacting Massive Particles [WIMPs]). And 70% of the Universe in their models consists of even more obscure dark energy, leaving only 5% for ordinary matter.
Creationist cosmology
In 1915, Einstein solved the problem of publishing his general theory of relativity. She showed that the anomalous precession is a consequence of how gravity distorts space and time and controls the motions of the planets when they are especially close to massive bodies, where the curvature of space is most pronounced.
Newtonian gravity is not a very accurate description of planetary motion. Especially when the curvature of space moves away from the Euclidean flatness. And general relativity explains the observed behavior almost exactly. Thus, neither dark matter, which some have suggested was in an invisible ring of matter around the Sun, nor the planet Vulcan itself, were needed to explain the anomaly.
Conclusions
In the early daysthe cosmological constant would be negligible. At later times, the density of matter will be essentially zero, and the universe will be empty. We live in that short cosmological epoch when both matter and vacuum are of comparable magnitude.
Within the matter component, apparently, there are contributions from both baryons and a non-baryon source, both of them are comparable (at least, their ratio does not depend on time). This theory wobbles under the weight of its unnaturalness, but nevertheless crosses the finish line way ahead of the competition, so well does it fit with the data.
In addition to confirming (or refuting) this scenario, the main challenge for cosmologists and physicists in the coming years will be to understand whether these seemingly unpleasant aspects of our universe are simply amazing coincidences or actually reflect basic structure that we don't yet understand.
If we are lucky, everything that seems unnatural now will serve as the key to a deeper understanding of fundamental physics.






