Plane in space. Location of planes in space

2024 Author: Angel Austin | [email protected]. Last modified: 2024-01-02 17:39

A plane is a geometric object whose properties are used when constructing projections of points and lines, as well as when calculating distances and dihedral angles between elements of three-dimensional figures. Let's consider in this article what equations can be used to study the location of planes in space.

Plane definition

Everyone intuitively imagines what object will be discussed. From a geometric point of view, a plane is a collection of points, any vectors between which must be perpendicular to some one vector. For example, if there are m different points in space, then m(m-1) / 2 different vectors can be made from them, connecting the points in pairs. If all vectors are perpendicular to some one direction, then this is a sufficient condition that all points m belong to the same plane.

General equation

In spatial geometry, a plane is described using equations that generally contain three unknown coordinates corresponding to the x, y and z axes. Toget the general equation in plane coordinates in space, suppose there is a vector n¯(A; B; C) and a point M(x₀; y₀; z_{0). Using these two objects, the plane can be uniquely defined.}

Indeed, suppose there is some second point P(x; y; z) whose coordinates are unknown. According to the definition given above, the vector MP¯ must be perpendicular to n¯, that is, the scalar product for them is equal to zero. Then we can write the following expression:

(n¯MP¯)=0 or

A(x-x₀) + B(y-y₀) + C(z-z₀₎₌₀

Opening the brackets and introducing a new coefficient D, we get the expression:

Ax + By + Cz + D=0 where D=-1(Ax₀+ By ₀+ Cz₀₎

This expression is called the general equation for the plane. It is important to remember that the coefficients in front of x, y and z form the coordinates of the vector n¯(A; B; C) perpendicular to the plane. It coincides with the normal and is a guide for the plane. To determine the general equation, it does not matter where this vector is directed. That is, the planes built on the vectors n¯ and -n¯ will be the same.

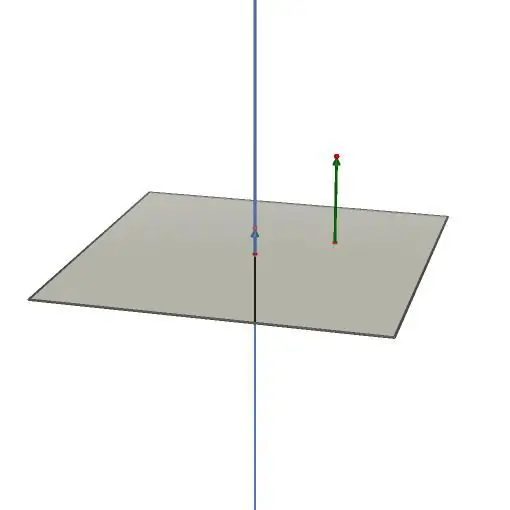
The figure above shows a plane, a vector normal to it, and a line perpendicular to the plane.

Segments cut off by the plane on the axes and the corresponding equation

The general equation allows using simple mathematical operations to determine, inat what points the plane will intersect the coordinate axes. It is important to know this information in order to have an idea about the position in space of the plane, as well as when depicting it in the drawings.

To determine the named intersection points, an equation in segments is used. It is so called because it explicitly contains the values of the lengths of the segments cut off by the plane on the coordinate axes, when counting from the point (0; 0; 0). Let's get this equation.

Write the general expression for the plane as follows:

Ax + By + Cz=-D

The left and right parts can be divided by -D without violating equality. We have:

A/(-D)x + B/(-D)y + C/(-D)z=1 or

x/(-D/A) + y/(-D/B) + z/(-D/C)=1

Design the denominators of each term with a new symbol, we get:

p=-D/A; q=-D/B; r=-D/C then

x/p + y/q + z/r=1

This is the equation mentioned above in segments. It follows from it that the value of the denominator of each term indicates the coordinate of the intersection with the corresponding axis of the plane. For example, it intersects the y-axis at the point (0; q; 0). This is easy to understand if you substitute the zero x and z coordinates into the equation.

Note that if there is no variable in the equation in the segments, this means that the plane does not intersect the corresponding axis. For example, given the expression:

x/p + y/q=1

This means that the plane will cut off the segments p and q on the x and y axes, respectively, but it will be parallel to the z axis.

Conclusion about the behavior of the plane whenthe absence of some variable in her equation is also true for an expression of a general type, as shown in the figure below.

Vector parametric equation

There is a third kind of equation that allows describing a plane in space. It is called a parametric vector because it is given by two vectors lying in the plane and two parameters that can take arbitrary independent values. Let's show how this equation can be obtained.

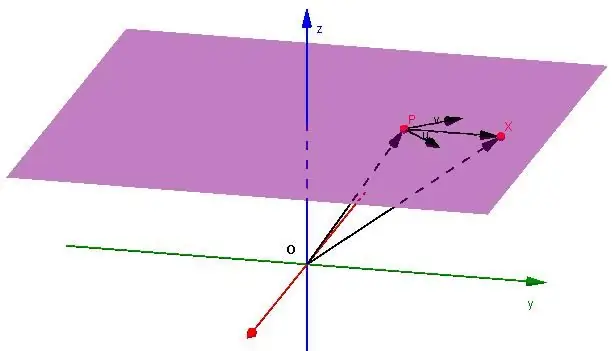
Suppose there are a couple of known vectors u ¯(a₁; b₁; c₁) and v¯(a₂; b₂; c₂). If they are not parallel, then they can be used to set a specific plane by fixing the beginning of one of these vectors at a known point M(x₀; y₀; z_{0). If an arbitrary vector MP¯ can be represented as a combination of linear vectors u¯ and v¯, then this means that the point P(x; y; z) belongs to the same plane as u¯, v¯. Thus, we can write the equality:}

MP¯=αu¯ + βv¯

Or writing this equality in terms of coordinates, we get:

(x; y; z)=(x₀; y₀; z₀) + α(a₁; b₁; c₁) + β(a ₂; b₂; c₂₎

The presented equality is a parametric vector equation for the plane. ATvector space in the plane u¯ and v¯ are called generators.

Next, when solving the problem, it will be shown how this equation can be reduced to a general form for a plane.

Angle between planes in space

Intuitively, planes in 3D space can either intersect or not. In the first case, it is of interest to find the angle between them. The calculation of this angle is more difficult than the angle between lines, since we are talking about a dihedral geometric object. However, the already mentioned guide vector for the plane comes to the rescue.

It is geometrically established that the dihedral angle between two intersecting planes is exactly equal to the angle between their guide vectors. Let's denote these vectors as n₁¯(a₁; b₁; c_{1) and n}2_¯(a2_{; b}2_{; c}2 _{). The cosine of the angle between them is determined from the scalar product. That is, the angle itself in the space between the planes can be calculated by the formula:}

φ=arccos(|(n₁¯n₂¯)|/(|n₁ ¯||n_2¯|))

Here the modulus in the denominator is used to discard the value of the obtuse angle (between intersecting planes it is always less than or equal to 90o).

In coordinate form, this expression can be rewritten as follows:

φ=arccos(|a₁a₂ + b₁b ₂ +c₁c₂|/(√(a₁² + b₁² + c₁²)√(a₂² + b₂² + c ₂²⁾⁾⁾

Planes perpendicular and parallel

If the planes intersect and the dihedral angle formed by them is 90o, then they will be perpendicular. An example of such planes is a rectangular prism or a cube. These figures are formed by six planes. At each vertex of the named figures there are three planes perpendicular to each other.

To find out whether the considered planes are perpendicular, it is enough to calculate the scalar product of their normal vectors. A sufficient condition for perpendicularity in the space of planes is the zero value of this product.

Parallel are called non-intersecting planes. Sometimes it is also said that parallel planes intersect at infinity. The condition of parallelism in the space of planes coincides with that condition for the direction vectors n₁¯ and n_{2¯. You can check it in two ways:}

Calculate the cosine of the dihedral angle (cos(φ)) using the scalar product. If the planes are parallel, then the value will be 1.

Try to represent one vector in terms of another by multiplying by some number, i.e. n₁¯=kn_{2¯. If this can be done, then the corresponding planes areparallel.}

The figure shows two parallel planes.

Now let's give examples of solving two interesting problems using the obtained mathematical knowledge.

How to get a general form from a vector equation?

This is a parametric vector expression for a plane. To make it easier to understand the flow of operations and the mathematical tricks used, consider a specific example:

(x; y; z)=(1; 2; 0) + α(2; -1; 1) + β(0; 1; 3)

Expand this expression and express the unknown parameters:

x=1 + 2α;

y=2 - α + β;

z=α + 3β

Then:

α=(x - 1)/2;

β=y - 2 + (x - 1)/2;

z=(x - 1)/2 + 3(y - 2 + (x - 1)/2)

Opening the brackets in the last expression, we get:

z=2x-2 + 3y - 6 or

2x + 3y - z - 8=0

We have obtained the general form of the equation for the plane specified in the problem statement in vector form

How to build a plane through three points?

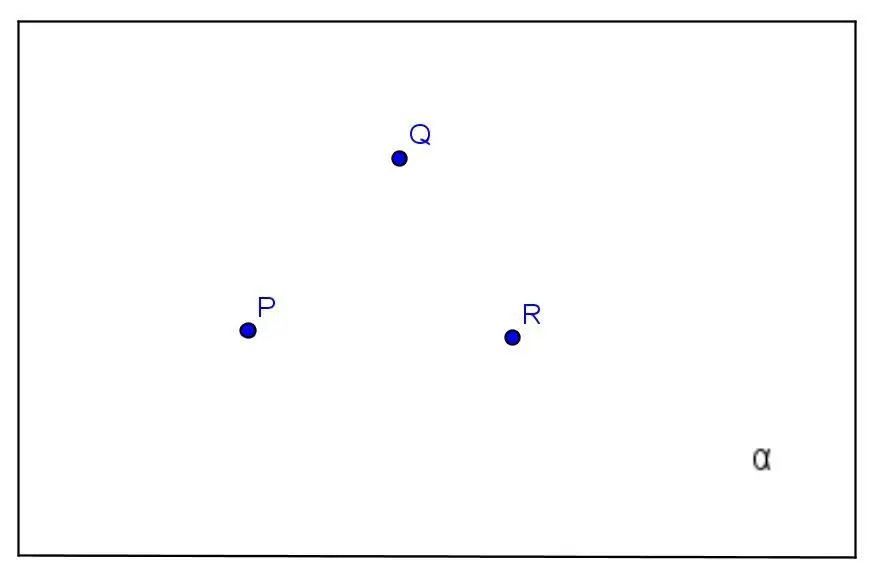
It is possible to draw a single plane through three points if these points do not belong to some single straight line. The algorithm for solving this problem consists in the following sequence of actions: