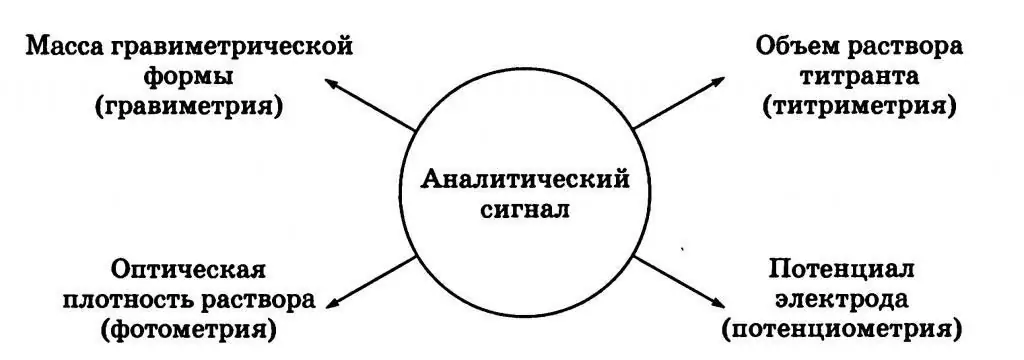
In mathematics and processing, the concept of an analytical signal (for short - C, AC) is a complex function that does not have negative frequency components. The real and imaginary parts of this phenomenon are real functions related to each other by the Hilbert transform. An analytical signal is a fairly common phenomenon in chemistry, the essence of which is similar to the mathematical definition of this concept.

Performances
Analytic representation of a real function is an analytic signal containing the original function and its Hilbert transform. This representation facilitates many mathematical manipulations. The main idea is that the negative frequency components of the Fourier transform (or spectrum) of a real function are redundant due to the Hermitian symmetry of such a spectrum. These negative frequency components can be discarded withoutloss of information, provided that you want to deal with a complex function instead. This makes certain feature attributes more accessible and makes it easier to derive modulation and demodulation techniques such as SSB.
Negative components
As long as the function being manipulated has no negative frequency components (ie it is still analytic), converting from complex back to real is simply a matter of discarding the imaginary part. The analytic representation is a generalization of the concept of a vector: while a vector is limited to a time-invariant amplitude, phase, and frequency, a qualitative analysis of an analytic signal allows for time-varying parameters.
Instantaneous amplitude, instantaneous phase and frequency are used in some applications to measure and detect local features of C. Another application of the analytical representation relates to the demodulation of modulated signals. Polar coordinates conveniently separate the effects of AM and phase (or frequency) modulation and effectively demodulate certain kinds.
Then a simple low-pass filter with real coefficients can cut off the part of interest. Another motive is to lower the maximum frequency, which lowers the minimum frequency for non-alias sampling. The frequency shift does not undermine the mathematical usefulness of the representation. So in this sense, downconverted is still analytic. However, the restoration of the real representationis no longer a simple matter of simply extracting the real component. Upconversion may be required, and if the signal is sampled (discrete time), interpolation (upsampling) may also be required to avoid aliasing.
Variables
The concept is well defined for single variable phenomena, which is usually temporary. This temporality confuses many beginning mathematicians. For two or more variables, analytic C can be defined in different ways, and two approaches are presented below.
The real and imaginary parts of this phenomenon correspond to two elements of a vector-valued monogenic signal, as defined for similar phenomena with one variable. However, monogenic can be extended to an arbitrary number of variables in a simple way, creating an (n + 1)-dimensional vector function for the case of n-variable signals.

Signal conversion
You can convert a real signal to an analytic one by adding an imaginary (Q) component, which is the Hilbert transform of the real component.
By the way, this is not new to its digital processing. One of the traditional ways to generate single sideband (SSB) AM, the phasing method, involves creating signals by generating a Hilbert transform of an audio signal in an analog resistor-capacitor network. Since it only has positive frequencies, it is easy to convert it to a modulated RF signal with only one sideband.

Definition formulas
Analytic signal expression is a holomorphic complex function defined on the boundary of the upper complex half-plane. The boundary of the upper half-plane coincides with the random, so C is given by the mapping fa: R → C. Since the middle of the last century, when Denis Gabor proposed in 1946 to use this phenomenon to study constant amplitude and phase, the signal has found many applications. The peculiarity of this phenomenon was emphasized [Vak96], where it was shown that only a qualitative analysis of the analytical signal corresponds to the physical conditions for amplitude, phase and frequency.
Latest achievements
During the last few decades there has been an interest in the study of the signal in many dimensions, motivated by problems arising in fields ranging from image / video processing to multidimensional oscillatory processes in physics, such as seismic, electromagnetic and gravitational waves. It has generally been accepted that, in order to correctly generalize analytic C (qualitative analysis) to the case of several dimensions, one must rely on an algebraic construction that extends the ordinary complex numbers in a convenient way. Such constructions are usually called hypercomplex numbers [SKE].
Finally, it should be possible to construct a hypercomplex analytic signal fh: Rd → S, where some general hypercomplex algebraic system is represented, which naturally extends all the required properties to obtain an instantaneous amplitude andphase.
Study
A number of papers are devoted to various issues related to the correct choice of the hypercomplex number system, the definition of the hypercomplex Fourier transform and fractional Hilbert transforms for studying the instantaneous amplitude and phase. Most of this work was based on properties of various spaces such as Cd, quaternions, Clearon algebras and Cayley-Dixon constructions.
Next, we will list only some of the works devoted to the study of the signal in many dimensions. As far as we know, the first works on the multivariate method were obtained in the early 1990s. These include Ell's work [Ell92] on hypercomplex transformations; Bulow's work on the generalization of the method of analytical reaction (analytical signal) to many measurements [BS01] and the work of Felsberg and Sommer on monogenic signals.

Further prospects
The hypercomplex signal is expected to extend all the useful properties we have in the 1D case. First of all, we must be able to extract and generalize the instantaneous amplitude and phase to the measurements. Second, the Fourier spectrum of a complex analytic signal is maintained only at positive frequencies, so we expect the hypercomplex Fourier transform to have its own hypervalued spectrum, which will only be maintained in some positive quadrant of the hypercomplex space. Because it is very important.
Third, conjugate parts of a complex conceptof the analytic signal are related to the Hilbert transform, and we can expect that the conjugate components in the hypercomplex space must also be related to some combination of the Hilbert transforms. And finally, indeed, a hypercomplex signal must be defined as an extension of some hypercomplex holomorphic function of several hypercomplex variables defined on the boundary of some form in a hypercomplex space.
We are addressing these issues in sequential order. First of all, we start by looking at the Fourier integral formula and show that the Hilbert transform to 1-D is related to the modified Fourier integral formula. This fact allows us to define the instantaneous amplitude, phase and frequency without any reference to hypercomplex number systems and holomorphic functions.
Modification of integrals
We continue by extending the modified Fourier integral formula to several dimensions, and determine all the necessary phase-shifted components that we can collect into instantaneous amplitude and phase. Second, we turn to the question of the existence of holomorphic functions of several hypercomplex variables. After [Sch93] it turns out that the commutative and associative hypercomplex algebra generated by a set of elliptic (e2i=−1) generators is a suitable space for a hypercomplex analytic signal to live, we call such a hypercomplex algebra the Schaefers space and denote itSd.
Therefore, the hypercomplex of analytic signals is defined as a holomorphic function on the boundary of the polydisk / upper half of the plane in some hypercomplex space, which we call the general Schaefers space, and denoted by Sd. We then observe the validity of the Cauchy integral formula for the functions Sd → Sd, which are computed over a hypersurface inside a polydisk in Sd and derive the corresponding fractional Hilbert transforms that relate the hypercomplex conjugate components. Finally, it turns out that the Fourier transform with values in Schaefers space is supported only at non-negative frequencies. Thanks to this article, you have learned what is an analytical signal.






