Primary school teachers are well aware that multiplication and division of multi-digit numbers in the 4th grade is difficult for children, because the basics of higher-order mathematical algorithms are being studied. Old methods are recognized as ineffective in teaching. This is due to the fact that the class rarely pays attention to dry facts, preferring to cope with the help of a calculator. The methodology described below will help to spark interest in children, distracting from the complex sequence of actions in parts.
Teaching Tips
Adults, for whom the calculation process seems elementary, do not always understand that this is new information for a child. Be patient and follow these guidelines to keep your environment friendly while exploring:
- Start learning math facts for a limited amount of time at a time. There is a big difference between finding the right answer and memorizing facts. If students are given a disproportionate amount of material, they are more likely to forgetthe most important information. Dividing multi-digit numbers in grade 4 involves bringing to automation using the multiplication table.
- Add more interesting facts after mastering. Children absorb new material almost instantly, just push their interest. Add fresh data when you notice that the old ones have taken hold. The learning process will succeed if you provide two or three things to analyze in a whole ocean of incomprehensible material.
- Cumulative practice is important. The solution of examples should be structured in such a way that facts previously considered learned continue to appear along with 2-3 new ones that are learned.
- Use the word chain as you practice so that you remember the multi-digit division sequence better. Ultimately, students will see 8×7 and say the answer themselves.
- Automatic mastery. With a gradual introduction of material with regular repetitions, children will very soon begin to give positive results without hesitation.
- Set your daily workout routine. The practical application of theoretical knowledge is effective only when it does not overload the human mind. Stretch material throughout the year. The study of facts is only a small part of the mathematical program, so bring the child's skill to the solution in the minimum amount of time. A standard daily routine is required to achieve this goal.
- Correct and correct mistakes. Whenever children hesitate or give a wrong answer,take a closer look at the situation. Make up a test, review the basics, ask questions about what was difficult and make sure that the repeated task will not cause difficulties. It is very important that the adjustment takes place as soon as possible, until the child forgets the technique.
- Classes should be short. It is a known fact that students cannot concentrate on training for more than 2-4 minutes. The practice can be done several times during the day, but should not last long.
Don't forget to motivate children, play interactive games or encourage them to inspire confidence in action. Support is the key to everything.
Mathematical terminology
Before moving on to dividing a multi-digit number by a single-digit number, you need to learn a few simple rules and terms:
- Every number other than zero is either negative or positive. If the sign is not displayed, then we automatically assign a plus in front.
- Each number in the problem has its own definition. For example, 6/2=3 - the first is divisible. This means that the number is broken into parts when applying mathematical basics. Next, 2 is the divisor and 3 is the product.
- If you are going through fractions, then emphasize that they are not the same thing, since there is a numerator and a denominator.
Some other rules:
- When you divide 0 by another number, the answer is always 0. For example: 0/2=0. This means that 0 candies are distributed equally among 2 children - each of them gets 0sweets.
- When you divide a number by 0, you cannot use this math solution. 2/0 is impossible. You have 2 cakes but no friends to share the sweet. Accordingly, there is no solution.
- When you divide by 1, the answer is the second number in the system. For example, 2/1=2. Two packets of marmalade will go to one boy.
- When you divide by 2, you halve the number. 2/2=1. So, the sweet will fall into the hands of both participants in the event. This rule also applies to other problems with similar numbers: 20/20=1. Twenty children get one candy.
- Divide in the correct order. 10/2=5, while 2/10=0.2. Agree that 10 gummies are much easier to distribute between two children than 2 for 10. The result is quite different.
But in order to master the division of a multi-digit number into a single-digit number in grade 4, it is not enough just to know the set of rules and move on to fixing the material, you need to repeat the opposite system of the function.
The principle of multiplying two numbers
Knowing the basics saves you from further problems with algebra. That is why you should pay attention to the previous lessons. In mathematics, the division of multi-digit numbers occurs on the basis of the study of the multiplication table.
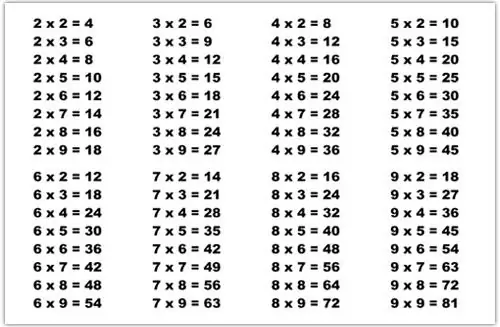
Thus, a structured plate will prompt the answer for basic operations with any number. It will come in handy not only in elementary school, but also when faced with higher mathematics. In other words, it must be fixed at the conscious level of the child in such a way thatto become as natural a process as eating and sleeping.
So, if you ask students to multiply 3×5, they can easily decompose the example into adding three fives. Instead of further suffering with large numbers, it is enough to remember the indicators of the plate.
The simplest multiplication method is to visualize numbers into objects. Suppose we need to know the answer in the case of 4×3. The first number can be represented as toy cars, and 3 as the number of groups we want to add to the collection.
Frequent multiplication practice in the future greatly facilitates the process of dividing multi-digit numbers. Pretty soon, the basics will take hold if you persevere and repeat the material regularly. It is recommended to create a line chart from 1 to 12 as shown in the picture:
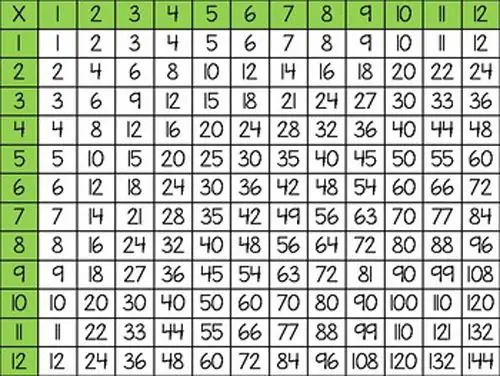
Using it is quite simple: slide your finger along the line from the desired number to the value of another. The chart can also be included in daily activities. Thanks to her, the child will be able to quickly orient himself and quickly consolidate the material.
First step: how to present
Now that you have begun the methods for dividing a multi-digit number by a single-digit number, you should clearly indicate the mathematical operation. The fact is that children are prone to elementary mistakes due to the fact that the material is new to them. Often they can divide by zero or confuse plus with minus. Be patient, because you did not immediately start with differentials. Explain that objects are divided into several groupsof the same number.
Once a simple understanding is established, move on to a gradual introduction to worksheets. Emphasize the importance of opposite functions. Division and multiplication are closely related, therefore solving examples of higher mathematics is impossible without the use of two computing techniques. Alternate the numbers in a logical sequence, swap them:
5×3=15, 3×5=15, 15/3=5, 15/5=3.
When the child goes through the theoretical lesson of dividing multi-digit numbers by a number, he will comprehend the whole concept, tracing the full structure. After that, proceed to the practical part. Demonstrate what signs indicate examples, listen to questions.
Start by practicing dividing multi-digit numbers by 1, 2, and 3, then work your way up to 9. Stock up on drafts for detailed analysis. As soon as the basic scheme of the solution becomes clear, the children will be connected to more difficult tasks.
Examples with the same sign
Now that we've covered all the details, it's important to look at the first dividing problem. Quite often, children get confused in the signs located in front of the numbers. How to represent 15/3? Both numbers are positive and will give the corresponding total. Answer: 5 or +5. It is not necessary to put a plus, since it is not customary to designate it.
But what to do if the examples of dividing multi-digit numbers have become with a minus? Just pay attention to its location.
So, -15/3=5 or +5.
Why did the sign turn out to bepositive? The point is that every division problem can be expressed as a multiplication. It follows that 2×3=6 is written as dividing 6/3=2. The sign alternation rule in the multiplication system tells us that 5×-3=-15. One way to label this as a dividing problem is -15/-3=5, which is the same as -15/-3.
Thus, it is advisable to highlight a new rule - the quotient of two negative numbers is positive.
Note that in both cases, the only difference from the arithmetic problem is that the child must predict the sign in advance, and then proceed to the calculation process. This method is effective and is used everywhere.
Another important rule is that a quotient with two identical signs will always give a positive value. Using this knowledge, children will quickly get used to the tasks.
Interactive games
To increase the speed of fixing the material, division of multi-digit numbers with cards in grade 4 is used. Talk to your child and emphasize that you should use the inverse multiplication function when calculating.
Use the flashcards below to help kids memorize and practice division facts, or create your own in a similar fashion.

Also, be sure to work out the values for 6 and 9, which are given to children with the greatest difficulty.
Recommendations for creating multi-digit division cards:
- Prepare tabular examples for all types of numbers by printing them onprinter.
- Cut the pages in half.
- Fold each card along the fold line.
- Stir and work with baby.
To achieve greater effect, you can print a similar stack, but to work out the multiplication technique.
Examples with remainders
Children who are first introduced to division will sooner or later make a mistake or divide a random number in such a way that the answer seems wrong to them. The remainder is used in more complex examples when it is impossible to do without it. Sometimes the product can consist of 0 integer and long digits behind a comma. It is important to explain to the child that such a written division of multi-digit numbers is normal.

Some problems cannot be solved without cuts, but that's another topic. The main thing in this case is to focus on the fact that sometimes the solution is real only with a remainder.
Division of large numbers: practice
Modern children quite often resort to mathematical solutions with the help of technology. When they learn to count correctly, they no longer need to worry about complex functions, especially if in the process of life they regularly repeat tabular values \u200b\u200band deftly use them. Divide sums can seem intimidating. In fact, like almost everything in mathematics, they will be logical. Let's consider one of the problems of dividing a multi-digit number by a single one in Grade 4.
Let's imagine that Tolya's car needs new tires. All four drive wheels and onespare should be replaced. The driver looked at a profitable option for a replacement costing 480 rubles, which also included fitting and disposal. How much will each tire cost?
The task before us is to calculate how much is 480/5. In other words, it's the same as saying how much 5 goes into 480.
We start by dividing 5 by 4 and immediately run into a problem because the first number is much higher than the second. Since we are only interested in whole numbers, we mentally set zero and highlight the numbers greater than 5 with an arc. At the moment it is 48.
The next step is to use the numerical value that would be included 5 times in 48. To answer this question, we turn to the multiplication table and look for the number in the column.
9×5=45 and 10×5=50.
The number is between the two given values. We are interested in 45, since it is less than 48 and it is realistic to subtract it without a negative result. So, 5 is included in 45 9 times, but not quite the way we wanted, because here the remainder is formed - 3.
Write 9 in the right column and solve 48-45=3. So 5×9=45, +3 to get 48.
Let the zero down so that 3 becomes 30. Now we need to divide 30 by 5, or find out how many times 5 goes into 30. Thanks to the table values, it's easy to find the answer - 6. Because 5 × 6=30. This allows share without a remainder. A more detailed solution technique is shown in the figure below.
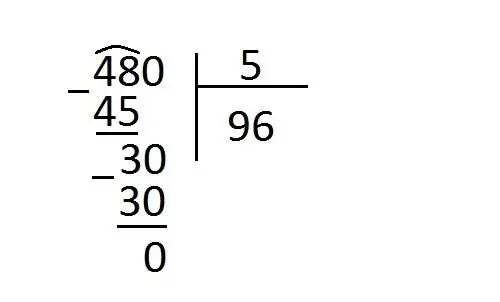
Since there is nothing else to share, we got 96 in the answer. Let's check in reverse.
480/5=96 and 96×5=480
Each new tire will cost Tolya 96 rubles.
How to teach division: tips for parents
Children aged 9-11 connect mathematical facts several times faster. For example, they understand that multiplication and division of multi-valued numbers closely intersect with each other, as 36/4 and 18 × 2 have the same calculus structure.

It will not be difficult for a child to determine the integrity of the solution, list multiples and explain the formation of the remainder. However, automation takes time, so we provide you with educational games to help you consolidate the material:
- Equal pouring. Fill the jug with water and let the children fill identical small cups by themselves until the jar is empty.
- Tell your child to cut the ribbon so they are the same length when wrapping gifts.
- Drawing. Creative games are a great way to reinforce the division of multi-digit numbers. Take a pencil and draw many lines on a piece of paper. Imagine that they are the legs of small monsters, having discussed their number in advance. The main task of the student is to divide them into an equal number.
- Distribution technique. Use plasticine or a sketch to create animals and pens and distribute them in equal numbers. This method helps with the concept of the features of division and crushing.
- Connect food. Sweets are always a strong motivator in childhood. Slicing the cake for the daybirthday, let the children count the number of people at home and tell them how many pieces you will need so that everyone has an equal share.
- Help around the house. Pretend that you need the participation of the child in everyday life. Ask them to hang up the laundry, indicating in advance that, regardless of the type of clothes, it takes 2 clothespins, and you have 20 in total. Give them a chance to guess how many items will fit and change the conditions each time.
- Dice game. Take three dice (or number cards) and roll two of them. Multiply the rolled dice to get the product, then divide by the remaining number. Discuss the presence of leftovers during the decision.
- Life situations. The child is old enough to go to the nearest store on his own, so give him pocket money regularly. Seriously talk about the fact that everyone sometimes meets with crises, where it is necessary to divide 100 rubles between two people. In this method, it is advisable to come up with a problem for the products. For example, chickens laid 50 eggs and the farmer needs to correctly divide their number into trays that can fit only 5 eggs. How many boxes will you need?
Conclusion
By understanding the basics of mathematical operations, children will stop worrying that they are not succeeding. The basics are laid in us from childhood, so do not be too lazy to pay attention to counting and division, because in the future algebra will only be more difficult and it will become impossible to master some equations without in-depth knowledge.






