Matrix is a special object in mathematics. It is depicted in the form of a rectangular or square table, composed of a certain number of rows and columns. In mathematics, there is a wide variety of types of matrices, differing in size or content. The numbers of its rows and columns are called orders. These objects are used in mathematics to organize the writing of systems of linear equations and conveniently search for their results. Equations using a matrix are solved using the method of Carl Gauss, Gabriel Cramer, minors and algebraic additions, as well as in many other ways. The basic skill when working with matrices is to bring them to a standard form. However, first, let's figure out what types of matrices are distinguished by mathematicians.
Null type
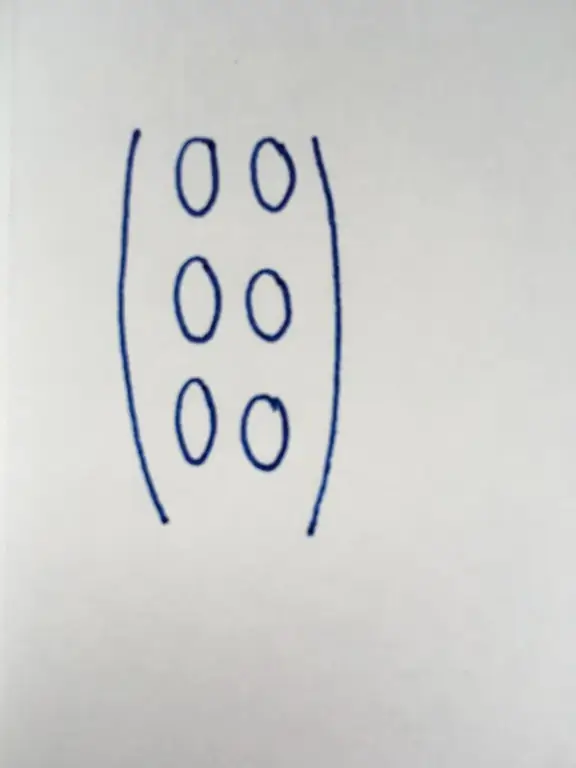
All components of this kind of matrix are zeros. Meanwhile, the number of its rows and columns is completely different.
Square type
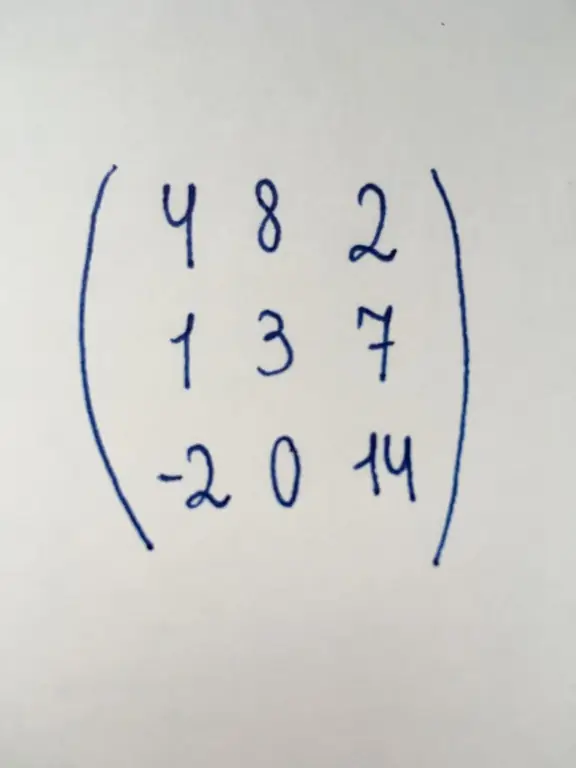
The number of columns and rows of this type of matrix is the same. In other words, it is a "square" shape table. The number of its columns (or rows) is called the order. Special cases are the existence of a matrix of the second order (matrix 2x2), fourth order (4x4), tenth (10x10), seventeenth (17x17) and so on.
Column vector
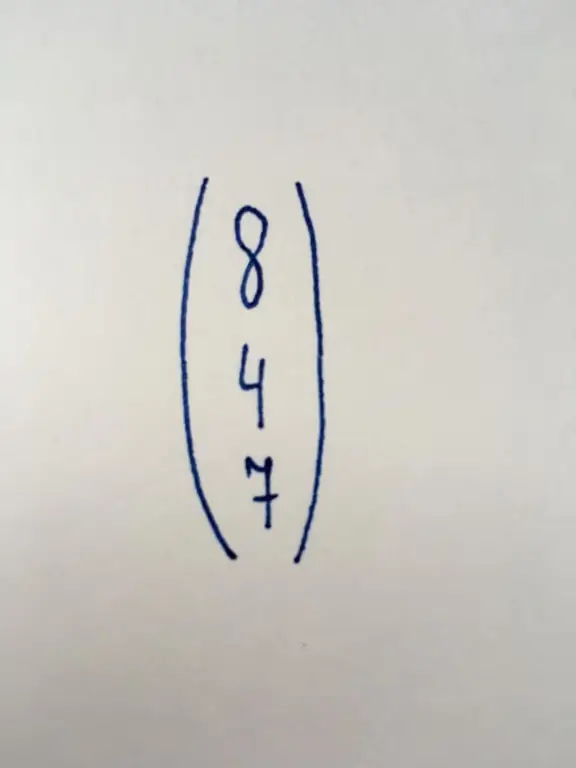
This is one of the simplest types of matrices, containing only one column, which includes three numerical values. It represents a series of free terms (numbers independent of variables) in systems of linear equations.
Row vector
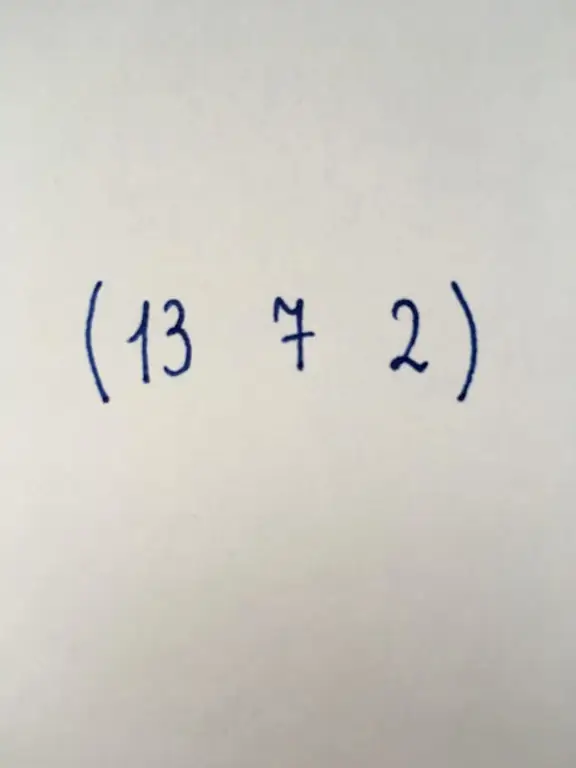
View similar to the previous one. Consists of three numerical elements, in turn organized in one line.
Diagonal type
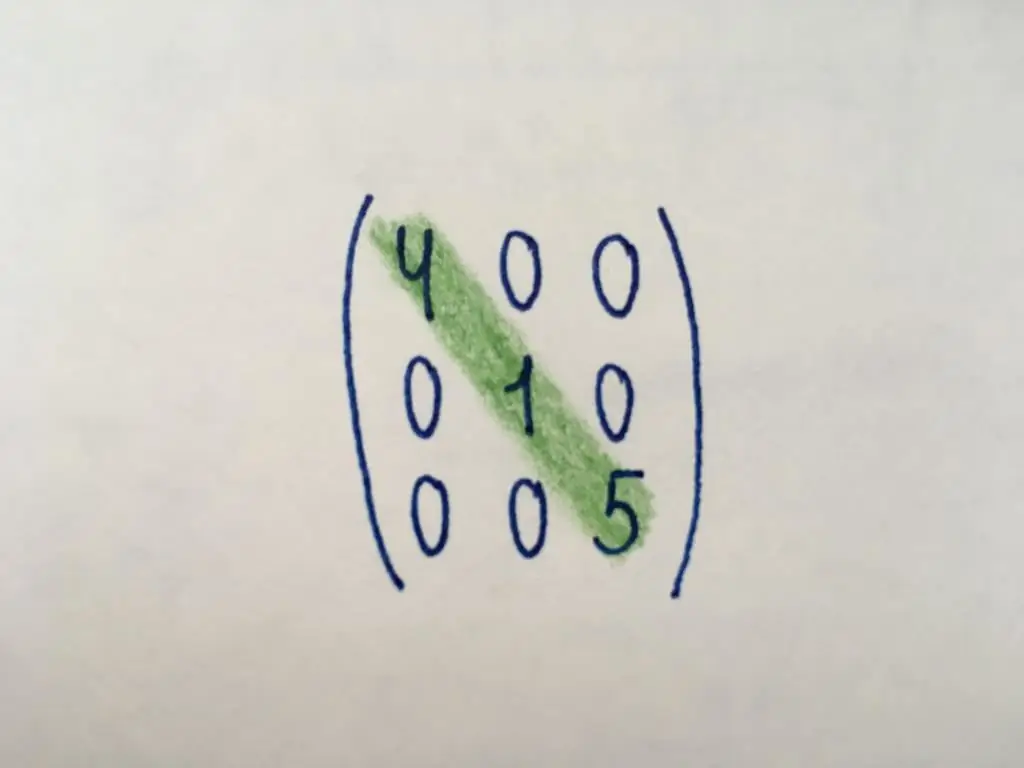
Only components of the main diagonal (highlighted in green) take numeric values in the diagonal form of the matrix. The main diagonal starts with the element in the upper left corner and ends with the element in the lower right, respectively. The rest of the components are zero. The diagonal type is only a square matrix of some order. Among matrices of the diagonal form, one can single out a scalar one. All its components take the same values.
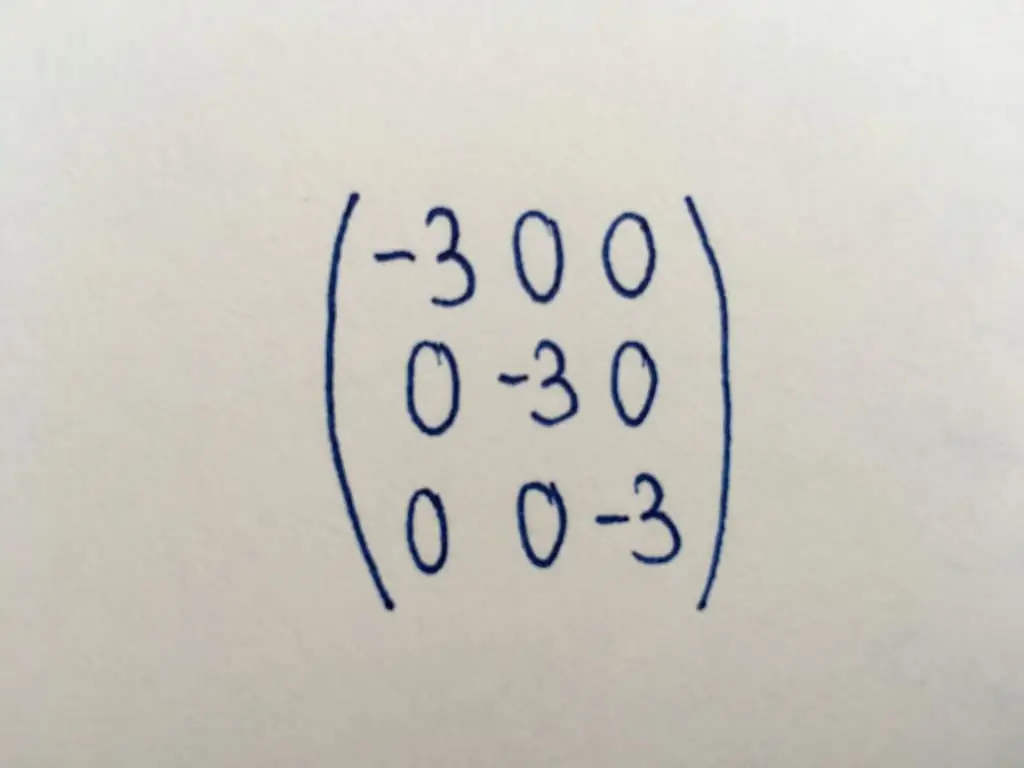
Identity matrix

A subspecies of the diagonal matrix. All its numerical values are units. Using a single type of matrix tables, perform its basic transformations or find a matrix inverse to the original one.
Canonical type
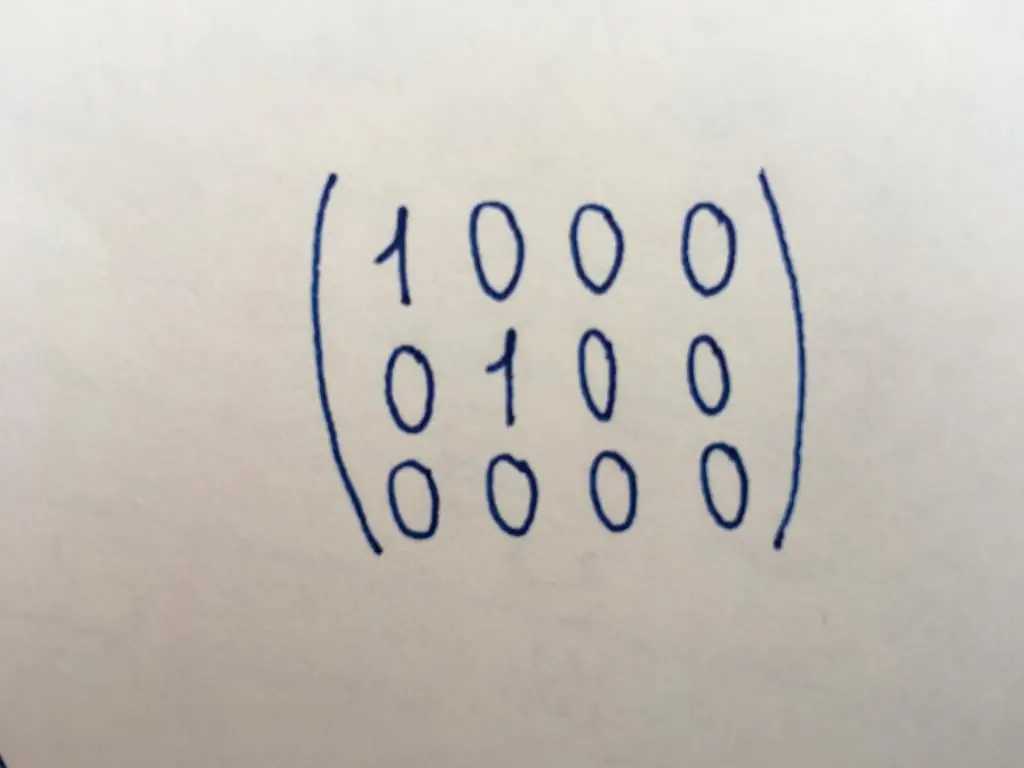
The canonical form of a matrix is considered one of the main ones; casting to it is often needed to work. The number of rows and columns in the canonical matrix is different, it does not necessarily belong to the square type. It is somewhat similar to the identity matrix, however, in its case, not all components of the main diagonal take on a value equal to one. There can be two or four main diagonal units (it all depends on the length and width of the matrix). Or there may be no units at all (then it is considered zero). The remaining components of the canonical type, as well as the elements of the diagonal and identity, are equal to zero.
Triangle type
One of the most important types of matrix, used when searching for its determinant and when performing simple operations. The triangular type comes from the diagonal type, so the matrix is also square. The triangular view of the matrix is divided into upper triangular and lower triangular.

In the upper triangular matrix (Fig. 1), only elements that are above the main diagonal take on a value equal to zero. The components of the diagonal itself and the part of the matrix below it contain numerical values.
In the lower triangular matrix (Fig. 2), on the contrary, the elements located in the lower part of the matrix are equal to zero.
Step Matrix

The view is necessary for finding the rank of a matrix, as well as for elementary operations on them (along with the triangular type). The step matrix is so named because it contains characteristic "steps" of zeros (as shown in the figure). In the stepped type, a diagonal of zeros is formed (not necessarily the main one), and all elements under this diagonal also have values equal to zero. A prerequisite is the following: if there is a zero row in the step matrix, then the remaining rows below it also do not contain numeric values.
Thus, we have considered the most important types of matrices needed to work with them. Now let's deal with the task of converting a matrix into the required form.
Reduce to triangular form
How to bring the matrix to a triangular form? Most often, in assignments, you need to convert a matrix into a triangular form in order to find its determinant, otherwise called the determinant. When performing this procedure, it is extremely important to "preserve" the main diagonal of the matrix, because the determinant of a triangular matrix is exactly the product of the components of its main diagonal. Let me also remind you of alternative methods for finding the determinant. The square-type determinant is found using special formulas. For example, you can use the triangle method. For other matrices, the method of decomposition by row, column, or their elements is used. You can also apply the method of minors and algebraic complements of the matrix.
DetailsLet's analyze the process of bringing a matrix to a triangular form using examples of some tasks.
Task 1
It is necessary to find the determinant of the presented matrix using the method of bringing it to a triangular form.

The matrix given to us is a square matrix of the third order. Therefore, to transform it into a triangular form, we need to nullify two components of the first column and one component of the second.
To bring it to a triangular form, start the transformation from the lower left corner of the matrix - from the number 6. To turn it to zero, multiply the first row by three and subtract it from the last row.
Important! The top line does not change, but remains the same as in the original matrix. You do not need to write a string four times the original one. But the values of the strings whose components need to be nullified are constantly changing.
Next, let's deal with the next value - the element of the second row of the first column, number 8. Multiply the first row by four and subtract it from the second row. We get zero.
Only the last value remains - the element of the third row of the second column. This is the number (-1). To turn it to zero, subtract the second from the first line.
Let's check:
detA=2 x (-1) x 11=-22.
So the answer to the task is -22.
Task 2
We need to find the determinant of the matrix by bringing it to a triangular form.

Represented matrixbelongs to the square type and is a matrix of the fourth order. This means that three components of the first column, two components of the second column, and one component of the third column must be zeroed.
Let's start its reduction from the element located in the lower left corner - from the number 4. We need to turn this number to zero. The easiest way to do this is to multiply the top row by four and then subtract it from the fourth row. Let's write down the result of the first stage of the transformation.
So, the component of the fourth line is set to zero. Let's move on to the first element of the third line, to the number 3. We perform a similar operation. Multiply by three the first line, subtract it from the third line and write the result.
Next, we see the number 2 in the second line. We repeat the operation: multiply the top row by two and subtract it from the second one.
We managed to set to zero all the components of the first column of this square matrix, except for the number 1, the element of the main diagonal that does not require transformation. Now it is important to save the resulting zeros, so we will perform transformations with rows, not columns. Let's move on to the second column of the presented matrix.
Let's start from the bottom again - from the element of the second column of the last row. This is the number (-7). However, in this case it is more convenient to start with the number (-1) - the element of the second column of the third row. To turn it to zero, subtract the second row from the third row. Then we multiply the second row by seven and subtract it from the fourth. We got zero instead of the element located in the fourth row of the second column. Now let's move on to the thirdcolumn.
In this column, we need to turn to zero only one number - 4. It's easy to do: just add the third to the last line and see the zero we need.
After all the transformations, we brought the proposed matrix to a triangular form. Now, to find its determinant, you only need to multiply the resulting elements of the main diagonal. We get: detA=1 x (-1) x (-4) x 40=160. Therefore, the solution is the number 160.
So, now the question of bringing the matrix to a triangular form will not make it difficult for you.
Reduction to stepped form
In elementary operations on matrices, the stepped form is less "demanded" than the triangular one. It is most commonly used to find the rank of a matrix (i.e., the number of its non-zero rows) or to determine linearly dependent and independent rows. However, the stepped matrix view is more versatile, as it is suitable not only for the square type, but for all others.
To reduce a matrix to a stepped form, you first need to find its determinant. For this, the above methods are suitable. The purpose of finding the determinant is to find out if it can be converted into a step matrix. If the determinant is greater or less than zero, then you can safely proceed to the task. If it is equal to zero, it will not work to reduce the matrix to a stepped form. In this case, you need to check if there are any errors in the record or in the matrix transformations. If there are no such inaccuracies, the task cannot be solved.
Let's see howbring the matrix to a stepped form using examples of several tasks.
Task 1. Find the rank of the given matrix table.

Before us is a square matrix of the third order (3x3). We know that in order to find the rank, it is necessary to reduce it to a stepped form. Therefore, we first need to find the determinant of the matrix. Using the triangle method: detA=(1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x 3 x 0) - (6 x 5 x 2)=12.
Determinant=12. It is greater than zero, which means that the matrix can be reduced to a stepped form. Let's start its transformations.
Let's start with the element of the left column of the third row - the number 2. Multiply the top row by two and subtract it from the third one. Thanks to this operation, both the element we need and the number 4 - the element of the second column of the third row - turned into zero.
Next, turn to zero the element of the second row of the first column - the number 3. To do this, multiply the top row by three and subtract it from the second one.
We see that the reduction resulted in a triangular matrix. In our case, the transformation cannot be continued, since the remaining components cannot be turned to zero.
So, we conclude that the number of rows containing numeric values in this matrix (or its rank) is 3. Answer to the task: 3.
Task 2. Determine the number of linearly independent rows of this matrix.
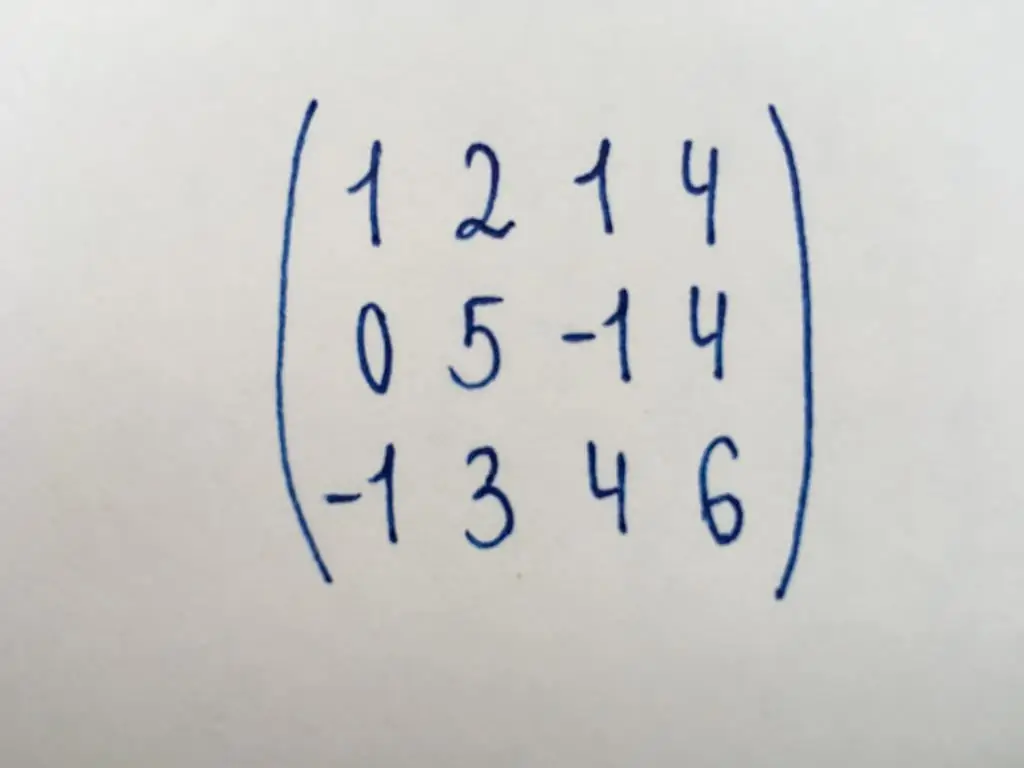
We need to find strings that cannot be reversed by any transformationsto zero. In fact, we need to find the number of non-zero rows, or the rank of the represented matrix. To do this, let's simplify it.
We see a matrix that does not belong to the square type. It has dimensions 3x4. Let's also start the cast from the element of the lower left corner - the number (-1).
Add the first line to the third one. Next, subtract the second from it to turn the number 5 to zero.
Further transformations are impossible. So, we conclude that the number of linearly independent lines in it and the answer to the task is 3.
Now bringing the matrix to a stepped form is not an impossible task for you.
On the examples of these tasks, we analyzed the reduction of a matrix to a triangular form and a stepped form. In order to nullify the desired values of matrix tables, in some cases it is required to show imagination and correctly transform their columns or rows. Good luck in math and working with matrices!






