Movement around the axis of rotation is one of the most common types of movement of objects in nature. In this article, we will consider this type of movement from the point of view of dynamics and kinematics. We also give formulas relating the main physical quantities.
Which movement are we talking about?

In the literal sense, we will talk about moving bodies around a circle, that is, about their rotation. A striking example of such movement is the rotation of the wheel of a car or bicycle while the vehicle is moving. Rotation around its axis of a figure skater performing complex pirouettes on ice. Or the rotation of our planet around the Sun and around its own axis inclined to the plane of the ecliptic.
As you can see, an important element of the considered type of movement is the axis of rotation. Each point of an arbitrary-shaped body makes circular motions around it. The distance from the point to the axis is called the radius of rotation. Many properties of the entire mechanical system depend on its value, for example, the moment of inertia, linear speed andothers.
Rotation dynamics

If the reason for the linear translational movement of bodies in space is the external force acting on them, then the reason for the movement around the axis of rotation is the external moment of force. This value is described as the vector product of the applied force F¯ and the distance vector from the point of its application to the axis r¯, that is:
M¯=[r¯F¯]
The action of the moment M¯ leads to the appearance of angular acceleration α¯ in the system. Both quantities are related to each other through some coefficient I by the following equality:
M¯=Iα¯
The value I is called the moment of inertia. It depends both on the shape of the body and on the distribution of mass inside it and on the distance to the axis of rotation. For a material point, it is calculated by the formula:
I=mr2
If the external moment of force is equal to zero, then the system retains its angular momentum L¯. This is another vector quantity, which, according to the definition, is equal to:
L¯=[r¯p¯]
Here p¯ is a linear momentum.
The law of conservation of moment L¯ is usually written as follows:
Iω=const
Where ω is the angular velocity. She will be discussed further in the article.
Rotation kinematics
Unlike dynamics, this branch of physics considers exclusively practical important quantities related to the change in time of the position of bodies inspace. That is, the objects of study of the kinematics of rotation are velocities, accelerations and angles of rotation.
First, let's introduce the angular velocity. It is understood as the angle through which the body makes a turn per unit of time. The formula for the instantaneous angular velocity is:
ω=dθ/dt
If the body rotates through equal angles for the same time intervals, then the rotation is called uniform. For him, the formula for the average angular velocity is valid:
ω=Δθ/Δt
Measured ω in radians per second, which in the SI system corresponds to reciprocal seconds (c-1).
In the case of non-uniform rotation, the concept of angular acceleration α is used. It determines the rate of change in time of the value ω, that is:
α=dω/dt=d2θ/dt2
Measured α in radians per square second (in SI - c-2).
If the body initially rotated uniformly at a speed ω0, and then began to increase its speed with a constant acceleration α, then such a movement can be described by the following formula:
θ=ω0t + αt2/2
This equality is obtained by integrating the angular velocity equations over time. The formula for θ allows you to calculate the number of revolutions that the system will make around the axis of rotation in time t.
Linear and angular speeds
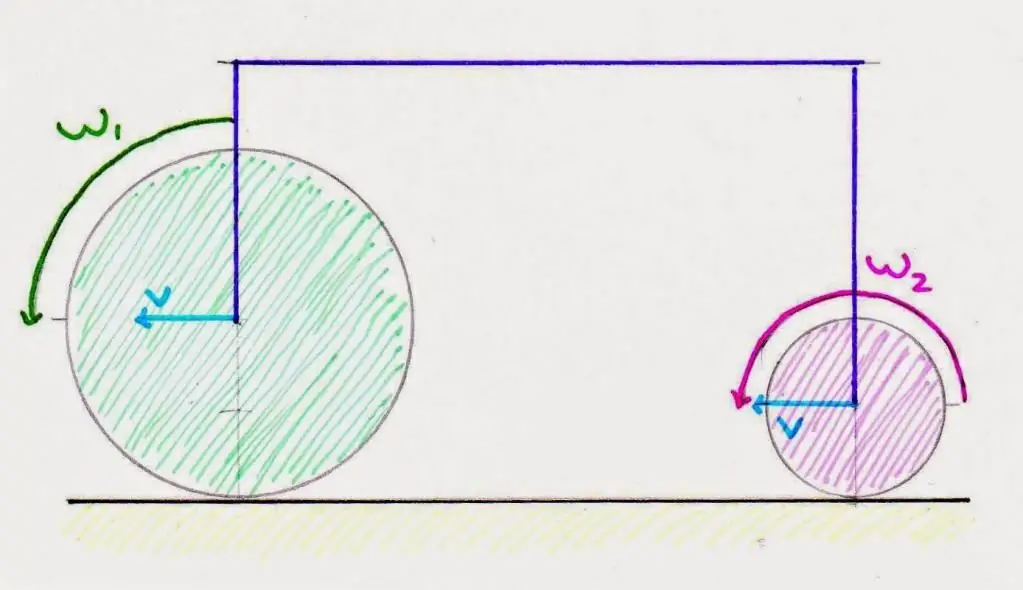
Both speeds with each otherconnected to another. When talking about the speed of rotation around an axis, they can mean both linear and angular characteristics.
Assume that some material point rotates around an axis at a distance r with a speed ω. Then its linear velocity v will be equal to:
v=ωr
The difference between linear and angular speed is significant. Thus, ω does not depend on the distance to the axis during uniform rotation, while the value of v increases linearly with increasing r. The latter fact explains why, with an increase in the radius of rotation, it is more difficult to keep the body on a circular trajectory (its linear velocity and, as a result, inertial forces increase).
The task of calculating the speed of rotation around its axis of the Earth
Everyone knows that our planet in the solar system performs two types of rotational motion:
- around its axis;
- around the star.
Compute the speeds ω and v for the first one.
Angular velocity is not difficult to determine. To do this, remember that the planet makes a complete revolution, equal to 2pi radians, in 24 hours (the exact value is 23 hours 56 minutes 4.1 seconds). Then the value of ω will be:
ω=2pi/(243600)=7, 2710-5rad/s
The calculated value is small. Let us now show how much the absolute value of ω differs from that for v.
Calculate the linear velocity v for points lying on the surface of the planet, at the latitude of the equator. Insofar asThe earth is an oblate ball, the equatorial radius is slightly larger than the polar. It is 6378 km. Using the formula for the connection of two speeds, we get:
v=ωr=7, 2710-56378000 ≈ 464 m/s
The resulting speed is 1670 km/h, which is greater than the speed of sound in air (1235 km/h).
The rotation of the Earth around its axis leads to the appearance of the so-called Coriolis force, which should be taken into account when flying ballistic missiles. It is also the cause of many atmospheric phenomena, such as the deviation of the direction of the trade winds to the west.






