What are the basic concepts of kinematics? What is this science and what does it study? Today we will talk about what kinematics is, what basic concepts of kinematics take place in tasks and what they mean. In addition, let's talk about the quantities that we most often deal with.
Kinematics. Basic concepts and definitions

First, let's talk about what it is. One of the most studied sections of physics in the school course is mechanics. It is followed in an indefinite order by molecular physics, electricity, optics, and some other branches, such as, for example, nuclear and atomic physics. But let's take a closer look at the mechanics. This branch of physics deals with the study of the mechanical motion of bodies. It establishes some patterns and studies its methods.
Kinematics as part of mechanics
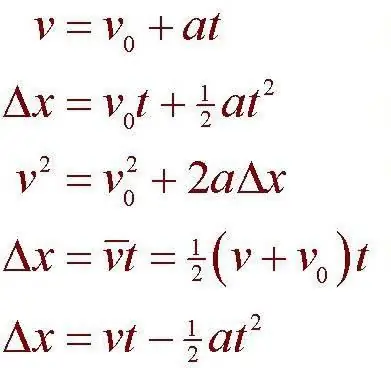
The latter is divided into three parts: kinematics, dynamics and statics. These three subsciences, if you can call them that, have some peculiarities. For example, statics studies the rules for the equilibrium of mechanical systems. An association with scales immediately comes to mind. Dynamics studies the laws of motion of bodies, but at the same time pays attention to the forces acting on them. But kinematics does the same, only forces are not taken into account. Consequently, the mass of those same bodies is not taken into account in the tasks.
Basic concepts of kinematics. Mechanical movement

The subject in this science is a material point. It is understood as a body, the dimensions of which, in comparison with a certain mechanical system, can be neglected. This so-called idealized body is akin to an ideal gas, which is considered in the section of molecular physics. In general, the concept of a material point, both in mechanics in general and in kinematics in particular, plays a rather important role. The most commonly considered so-called translational movement.
What does it mean and what could it be?
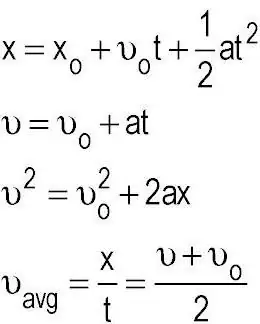
Usually movements are divided into rotational and translational. The basic concepts of the kinematics of translational motion are mainly related to the quantities used in the formulas. We will talk about them later, but for now let's return to the type of movement. It is clear that if we are talking about rotational, then the body is spinning. Accordingly, the translational movement will be called the movement of the body in a plane or linearly.
Theoretical basis for solving problems

Kinematics, the basic concepts and formulas of which we are considering now, has a huge number of tasks. This is achieved through the usual combinatorics. One method of diversity here is to change unknown conditions. One and the same problem can be presented in a different light by simply changing the purpose of its solution. It is required to find distance, speed, time, acceleration. As you can see, there are a whole lot of options. If we include the conditions of free fall here, the space becomes simply unimaginable.
Values and formulas
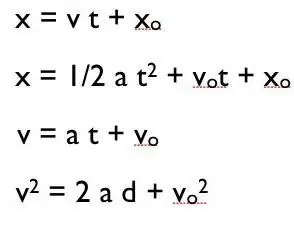
First of all, let's make one reservation. As is known, quantities can have a dual nature. On the one hand, a certain numerical value may correspond to a certain value. But on the other hand, it can also have a direction of distribution. For example, a wave. In optics, we are faced with such a concept as wavelength. But if there is a coherent light source (the same laser), then we are dealing with a beam of plane polarized waves. Thus, the wave will correspond not only to a numerical value indicating its length, but also to a given direction of propagation.
Classic example
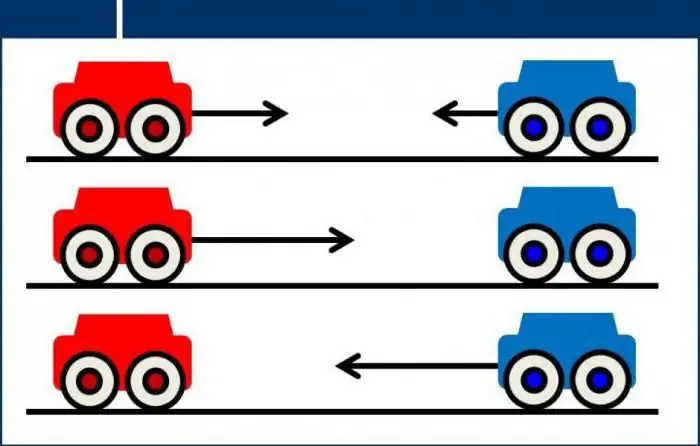
Such cases are an analogy in mechanics. Let's say a cart is rolling in front of us. Bythe nature of the movement, we can determine the vector characteristics of its speed and acceleration. It will be a little more difficult to do this when moving forward (for example, on a flat floor), so we will consider two cases: when the cart rolls up and when it rolls down.
So let's imagine that the cart is going up a slight incline. In this case, it will slow down if no external forces act on it. But in the reverse situation, namely, when the cart rolls down, it will accelerate. The speed in two cases is directed towards where the object is moving. This should be taken as a rule. But acceleration can change the vector. When decelerating, it is directed in the direction opposite to the velocity vector. This explains the slowdown. A similar logical chain can be applied to the second situation.
Other values
We just talked about the fact that in kinematics they operate not only with scalar quantities, but also with vector ones. Now let's take it one step further. In addition to speed and acceleration, when solving problems, such characteristics as distance and time are used. By the way, the speed is divided into initial and instantaneous. The first of them is a special case of the second. Instantaneous speed is the speed that can be found at any given time. And with the initial, probably, everything is clear.
Task
A large part of the theory was studied by us earlier in the previous paragraphs. Now it remains only to give the basic formulas. But we will do even better: we will not just consider the formulas, but also apply them when solving the problem in order tofinalize the acquired knowledge. Kinematics uses a whole set of formulas, combining which, you can achieve everything you need to solve. Here is a problem with two conditions to understand this completely.
A cyclist slows down after crossing the finish line. It took him five seconds to come to a complete stop. Find out with what acceleration he slowed down, as well as how much braking distance he managed to cover. The braking distance is considered linear, the final speed is taken equal to zero. At the moment of crossing the finish line, the speed was 4 meters per second.
In fact, the task is quite interesting and not as simple as it might seem at first glance. If we try to take the distance formula in kinematics (S=Vot + (-) (at ^ 2/2)), then nothing will come of it, since we will have an equation with two variables. How to proceed in such a case? We can go two ways: first calculate the acceleration by substituting the data into the formula V=Vo - at, or express the acceleration from there and substitute it into the distance formula. Let's use the first method.
So, the final velocity is zero. Initial - 4 meters per second. By transferring the corresponding quantities to the left and right sides of the equation, we achieve an expression for acceleration. Here it is: a=Vo/t. Thus, it will be equal to 0.8 meters per second squared and will have a braking character.
Go to the distance formula. We simply substitute data into it. We get the answer: the stopping distance is 10 meters.






