The topic of our today's article will be the kinematics of a material point. What is it all about? What concepts appear in it and what definition should be given to this term? We will try to answer these and many other questions today.
Definition and concept
Kinematics of a material point is nothing more than a subsection of physics called "mechanics". She, in turn, studies the patterns of motion of certain bodies. The kinematics of a material point also deals with this problem, but does not do it in a general way. In fact, this subsection studies methods that allow you to describe the movement of bodies. In this case, only the so-called idealized bodies are suitable for research. These include: a material point, an absolutely rigid body and an ideal gas. Let's consider the concepts in more detail. We all know from the school bench that it is customary to call a material point a body, the dimensions of which in a given situation can be neglected. By the way, the kinematics of the translational motion of a material point for the first time beginsappear in seventh grade physics textbooks. This is the simplest branch, so it is most convenient to start acquaintance with science with its help. A separate question is what are the elements of the kinematics of a material point. There are quite a lot of them, and conditionally they can be divided into several levels with different complexity for understanding. If we talk, for example, about the radius vector, then, in principle, there is nothing prohibitively complicated in its definition. However, you will agree that it will be much easier for a student to understand it than for a student of middle or high school. And to be honest, there is no need to explain the features of this term to high school students.
A brief history of the creation of kinematics
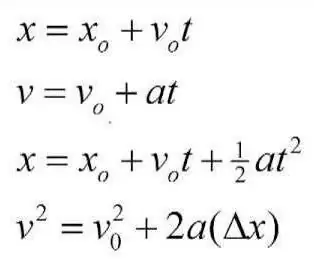
Many, many years ago, the great scientist Aristotle devoted the lion's share of his free time to the study and description of physics as a separate science. He also worked on kinematics, trying to present its main theses and concepts, one way or another used in attempts to solve practical and even everyday problems. Aristotle gave the initial ideas about what the elements of the kinematics of a material point are. His works and works are very valuable for all mankind. Nevertheless, in his conclusions, he made a considerable number of errors, and the reason for this were certain misconceptions and miscalculations. At one time, another scientist, Galileo Galilei, became interested in the works of Aristotle. One of the fundamental theses put forward by Aristotle was that the movement of a bodyoccurs only if it is acted upon by some force, determined by intensity and direction. Galileo proved that this was a mistake. The force will affect the movement speed parameter, but no more. The Italian showed that force is the cause of acceleration, and it can only arise mutually with it. Galileo Galilei also paid considerable attention to the study of the process of free fall, deriving the corresponding patterns. Probably everyone remembers his famous experiments, which he conducted on the Leaning Tower of Pisa. The physicist Ampère also used the basics of kinematic solutions in his works.
Initial concepts
As mentioned earlier, kinematics is the study of ways to describe the motion of idealized objects. In this case, the basics of mathematical analysis, ordinary algebra and geometry can be applied in practice. But what concepts (precisely concepts, and not definitions for parametric quantities) underlie this subsection of physics? First, everyone should clearly understand that the kinematics of the translational motion of a material point considers motion without taking into account force indicators. That is, to solve the corresponding problems, we do not need formulas related to force. It is not taken into account by kinematics, no matter how many of them there are - one, two, three, at least several hundred thousand. Nevertheless, the existence of acceleration is still provided. In a number of problems, the kinematics of the movement of a material point prescribes to determine the magnitude of the acceleration. However, the causes of this phenomenon (that is, the forces andtheir nature) are not considered but omitted.
Classification
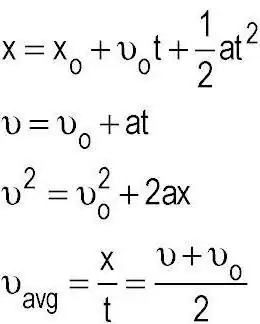
We found out that kinematics explores and applies methods for describing the movement of bodies without regard to the forces acting on them. By the way, another subsection of mechanics, which is called dynamics, deals with such a task. Already there, Newton's laws are applied, which allow in practice to determine quite a lot of parameters with a small amount of known initial data. The basic concepts of the kinematics of a material point are space and time. And in connection with the development of science both in general and in this area, the question arose about the appropriateness of using such a combination.
From the very beginning there was classical kinematics. We can say that it is characterized not only by the presence of both temporal and spatial gaps, but also their independence from the choice of one or another frame of reference. By the way, we will talk about this a little later. Now let's just explain what we are talking about. In this case, a segment will be considered a spatial interval, and a time interval will be considered a temporal interval. Everything seems to be clear. So, these gaps will be considered in classical kinematics as absolute, invariant, in other words, independent of the transition from one frame of reference to another. Whether business relativistic kinematics. In it, the gaps during the transition between reference systems can change. It would even be more correct to say that they cannot, but they must, probably. Because of this, the simultaneity of the tworandom events also becomes relative and subject to special consideration. That is why in relativistic kinematics two concepts - space and time - are combined into one.
Kinematics of a material point: speed, acceleration and other quantities
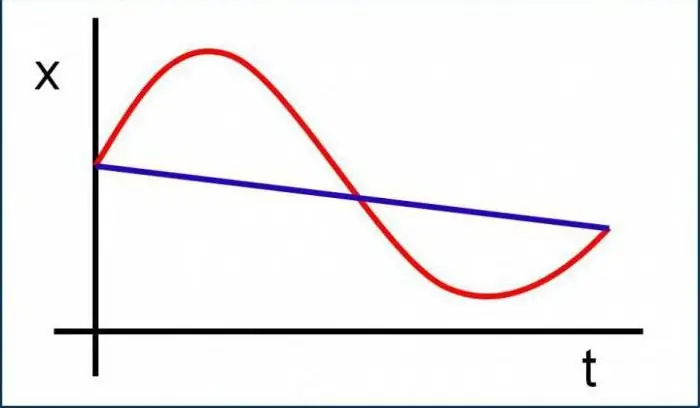
In order to understand at least a little this subsection of physics, you need to navigate the most important concepts, know the definitions and imagine what this or that quantity is in general terms. There is nothing difficult in this, in fact, everything is very easy and simple. Consider, perhaps, to begin with, the basic concepts used in kinematics problems.
Movement

Mechanical movement we will consider the process during which one or another idealized object changes its position in space. In this case, we can say that the change occurs relative to other bodies. It is also necessary to take into account the fact that the establishment of a certain time interval between two events occurs simultaneously. For example, it will be possible to isolate a certain interval formed during the time elapsed between the body arriving from one position to another. We also note that the bodies in this case can and will interact with each other, according to the general laws of mechanics. This is exactly what the kinematics of a material point most often operates with. The reference system is the next concept that is inextricably linked with it.
Coordinates
They can be called ordinary data that allows you to determine the position of the body at one time or another. Coordinates are inextricably linked with the concept of a reference system, as well as the coordinate grid. Most often they are a combination of letters and numbers.
Radius vector
From the name it should already be clear what it is. Nevertheless, let's talk about this in more detail. If a point moves along a certain trajectory, and we know exactly the beginning of a particular reference system, then we can draw a radius vector at any time. It will connect the initial position of the point to the instantaneous or final position.
Trajectory
It will be called a continuous line, which is laid as a result of the movement of a material point in a particular reference system.
Speed (both linear and angular)
This is a value that can tell how fast the body goes through a particular distance interval.
Acceleration (both angular and linear)
Shows by what law and how intensively the speed parameter of the body changes.
Perhaps, here they are - the main elements of the kinematics of a material point. It should be noted that both velocity and acceleration are vector quantities. And this means that they not only have some indicative value, but also a certain direction. By the way, they can be directed both in one direction and in opposite directions. In the first case, the body will accelerate, in the second it will slow down.
Simple tasks
Kinematics of a material point (velocity, acceleration and distance in which are practically fundamental concepts) includes not only a huge number of tasks, but many of their different categories. Let's try to solve a rather simple problem by determining the distance traveled by the body.
Suppose the conditions we have on hand are as follows. The driver's car is at the starting line. The operator gives the go-ahead with the flag, and the car abruptly takes off. Determine if she can set a new record in the competition of racers, if the next leader covered a distance of one hundred meters in 7.8 seconds. Take the acceleration of the car equal to 3 meters divided by a second squared.
So, how to solve this problem? It is quite interesting, since we are required not to “dry” determine certain parameters. It is brightened up with turns and a certain situation, which diversifies the process of solving and searching for indicators. But what should we be guided by before approaching the task?
1. The kinematics of a material point provides for the use of acceleration in this case.
2. The solution is assumed using the distance formula, since its numerical value appears in the conditions.
The problem is actually solved quite simply. To do this, we take the distance formula: S=VoT + (-) AT ^ 2/2. What is the point? We need to find out how long the rider will cover the designated distance, and then compare the figure with the record to find out if he beats it or not. To do this, allocate time, we obtain the formulafor him: AT^2 + 2VoT - 2S. This is nothing more than a quadratic equation. But the car takes off, which means that the initial speed will be 0. When solving the equation, the discriminant will be equal to 2400. To find the time, you need to take the root. Let's do it to the second decimal place: 48.98. Find the root of the equation: 48.98/6=8.16 seconds. It turns out that the driver will not be able to beat the existing record.






