To understand what the extremum points of a function are, it is not at all necessary to know about the presence of the first and second derivatives and understand their physical meaning. First you need to understand the following:
- function extrema maximize or, conversely, minimize the value of the function in an arbitrarily small neighborhood;
- There should not be a function break at the extremum point.

And now the same, only in plain language. Look at the tip of a ballpoint pen. If the pen is placed vertically, with the writing end up, then the very middle of the ball will be the extreme point - the highest point. In this case, we talk about the maximum. Now, if you turn the pen with the writing end down, then at the middle of the ball there will already be a minimum of the function. With the help of the figure given here, you can imagine the listed manipulations for a stationery pencil. So, the extrema of a function are always critical points: its maxima or minima. The adjacent section of the chart can be arbitrarily sharp or smooth, but it must exist on both sides, only in this case the point is an extremum. If the chart is present only on one side, this point will not be an extremum even if on one sideextremum conditions are met. Now let's study the extrema of the function from a scientific point of view. In order for a point to be considered an extremum, it is necessary and sufficient that:
- the first derivative was equal to zero or did not exist at the point;
- the first derivative changed its sign at this point.
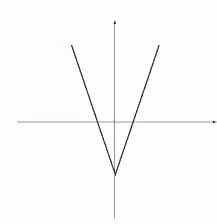
The condition is interpreted somewhat differently from the point of view of higher-order derivatives: for a function differentiable at a point, it is sufficient that there is an odd-order derivative that is not equal to zero, while all lower-order derivatives must exist and be equal to zero. This is the simplest interpretation of theorems from textbooks of higher mathematics. But for the most ordinary people, it is worth explaining this point with an example. The basis is an ordinary parabola. Immediately make a reservation, at the zero point it has a minimum. Just a little bit of math:
- first derivative (X2)|=2X, for zero point 2X=0;
- second derivative (2X)|=2, for zero point 2=2.
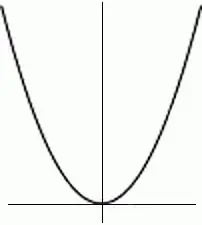
This is a simple illustration of the conditions that determine the extremums of the function both for first-order derivatives and for higher-order derivatives. We can add to this that the second derivative is just the same derivative of an odd order, unequal to zero, which was discussed a little higher. When it comes to extrema of a function of two variables, the conditions must be met for both arguments. Whengeneralization occurs, then partial derivatives are used. That is, it is necessary for the presence of an extremum at a point that both first-order derivatives be equal to zero, or at least one of them does not exist. For the sufficiency of the presence of an extremum, an expression is investigated, which is the difference between the product of second-order derivatives and the square of the mixed second-order derivative of the function. If this expression is greater than zero, then there is an extremum, and if there is zero, then the question remains open, and additional research is needed.






