Every person during his life encounters bodies that are in one of the three aggregate states of matter. The simplest state of aggregation to study is gas. In the article, we will consider the concept of an ideal gas, give the equation of state of the system, and also pay some attention to the description of the absolute temperature.
Gas state of matter
Each student has a good idea of what state of matter they are talking about when they hear the word "gas". This word is understood as a body that is capable of occupying any volume provided to it. It is not able to keep its shape, because it cannot resist even the slightest external influence. Also, gas does not retain volume, which distinguishes it not only from solids, but also from liquids.
Like a liquid, a gas is a fluid substance. In the process of motion of solid bodies in gases, the latter impede this motion. The resulting force is called resistance. Its value depends onvelocity of the body in the gas.
Strong examples of gases are air, natural gas used for heating homes and cooking, inert gases (Ne, Ar) used to fill advertising glow tubes or used to create an inert (non-aggressive, protective) environment when welding.
Ideal gas
Before proceeding to the description of gas laws and the equation of state, you should understand well the question of what an ideal gas is. This concept is introduced in molecular kinetic theory (MKT). An ideal gas is any gas that satisfies the following characteristics:
- The particles that form it do not interact with each other except for direct mechanical collisions.
- As a result of the collision of particles with the walls of the vessel or between themselves, their kinetic energy and momentum are conserved, that is, the collision is considered absolutely elastic.
- Particles have no dimensions, but have a finite mass, that is, they are similar to material points.
It is natural that any gas is not ideal, but real. Nevertheless, for solving many practical problems, these approximations are quite valid and can be used. There is a general empirical rule that says: regardless of the chemical nature, if a gas has a temperature above room temperature and a pressure of the order of atmospheric or lower, then it can be considered ideal with high accuracy and can be used to describe it.formula of the ideal gas equation of state.
Clapeyron-Mendeleev law
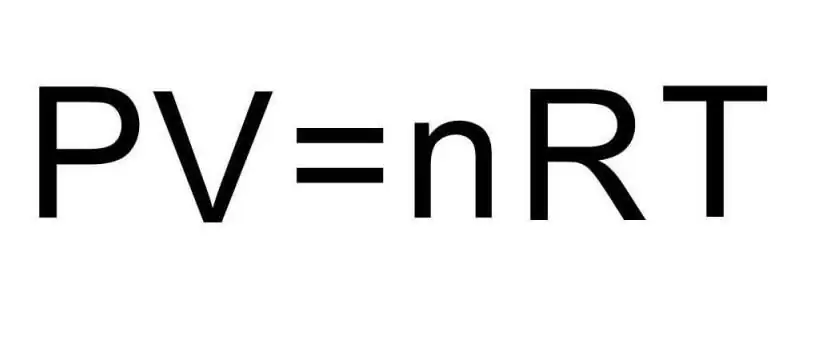
Transitions between different aggregate states of matter and processes within a single aggregate state are handled by thermodynamics. Pressure, temperature and volume are three quantities that uniquely define any state of a thermodynamic system. The formula for the equation of state of an ideal gas combines all three of these quantities into a single equality. Let's write this formula:
PV=nRT
Here P, V, T - pressure, volume, temperature, respectively. The value of n is the amount of substance in moles, and the symbol R denotes the universal constant of gases. This equality shows that the greater the product of pressure and volume, the greater must be the product of the amount of substance and temperature.

The formula for the equation of state of a gas is called the Clapeyron-Mendeleev law. In 1834, the French scientist Emile Clapeyron, summarizing the experimental results of his predecessors, came to this equation. However, Clapeyron used a number of constants, which Mendeleev later replaced with one - the universal gas constant R (8, 314 J / (molK)). Therefore, in modern physics, this equation is named after the names of French and Russian scientists.

Other Equation Forms
Above, we wrote the Mendeleev-Clapeyron equation of state for an ideal gas in the generally accepted andconvenient form. However, in problems in thermodynamics, a slightly different form may often be required. Three more formulas are written below, which directly follow from the written equation:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
These three equations are also universal for an ideal gas, only in them such quantities as mass m, molar mass M, density ρ and the number of particles N that make up the system appear. The symbol kB here denotes the Boltzmann constant (1, 3810-23J/K).
Boyle-Mariotte Law
When Clapeyron drew up his equation, he was based on gas laws that had been discovered experimentally several decades earlier. One of them is the Boyle-Mariotte law. It reflects an isothermal process in a closed system, as a result of which such macroscopic parameters as pressure and volume change. If we put T and n constant in the equation of state for an ideal gas, then the gas law will then take the form:
P1V1=P2V 2
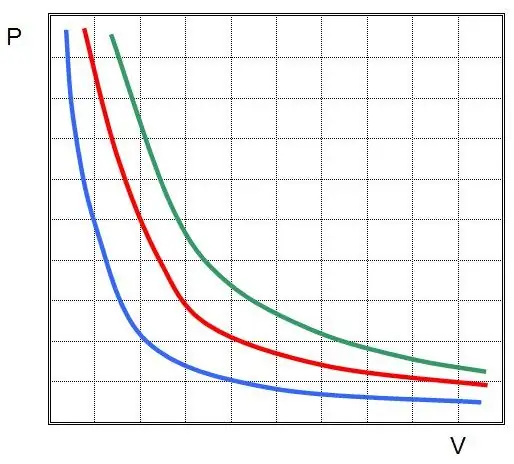
This is the Boyle-Mariotte law, which says that the product of pressure and volume is preserved during an arbitrary isothermal process. In this case, the values P and V themselves change.
If you plot P(V) or V(P), then the isotherms will be hyperbolas.
Charles and Gay-Lussac's laws
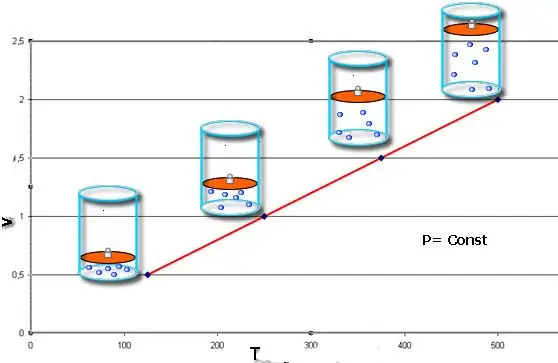
These laws mathematically describe isobaric and isochoricprocesses, that is, such transitions between the states of a gas system, in which pressure and volume are conserved, respectively. Charles' law can be mathematically written as follows:
V/T=const when n, P=const.
Gay-Lussac's law is written as follows:
P/T=const when n, V=const.
If both equalities are presented as a graph, then we will get straight lines that are inclined at some angle to the abscissa axis. This type of graph indicates a direct proportionality between volume and temperature at constant pressure and between pressure and temperature at constant volume.
Note that all three considered gas laws do not take into account the chemical composition of the gas, as well as the change in its amount of matter.
Absolute temperature
In everyday life, we are used to using the Celsius temperature scale, since it is convenient for describing the processes around us. So, water boils at 100 oC and freezes at 0 oC. In physics, this scale turns out to be inconvenient, therefore, the so-called absolute temperature scale, which was introduced by Lord Kelvin in the middle of the 19th century, is used. In accordance with this scale, the temperature is measured in Kelvin (K).
It is believed that at a temperature of -273, 15 oC there are no thermal vibrations of atoms and molecules, their forward movement stops completely. This temperature in degrees Celsius corresponds to absolute zero in Kelvin (0 K). From this definitionthe physical meaning of absolute temperature follows: it is a measure of the kinetic energy of the particles that make up matter, for example, atoms or molecules.
Besides the above physical meaning of absolute temperature, there are other approaches to understanding this quantity. One of them is the mentioned gas law of Charles. Let's write it in the following form:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
The last equality says that at a certain amount of substance in the system (for example, 1 mol) and a certain pressure (for example, 1 Pa), the gas volume uniquely determines the absolute temperature. In other words, an increase in the gas volume under the indicated conditions is possible only due to an increase in temperature, and a decrease in volume indicates a decrease in the value of T.
Recall that, unlike Celsius temperature, absolute temperature cannot be negative.
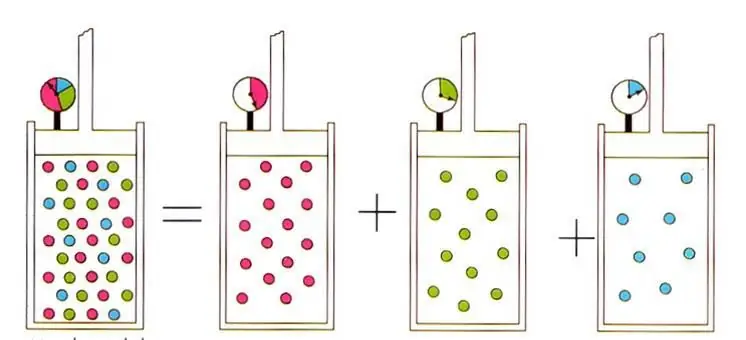
Avogadro principle and gas mixtures
In addition to the above gas laws, the equation of state for an ideal gas also leads to the principle discovered by Amedeo Avogadro at the beginning of the 19th century, which bears his last name. This principle establishes that the volume of any gas at constant pressure and temperature is determined by the amount of substance in the system. The corresponding formula looks like this:
n/V=const when P, T=const.
The written expression leads to the well-known in ideal gas physics D alton's law for gas mixtures. Thisthe law states that the partial pressure of a gas in a mixture is uniquely determined by its atomic fraction.
Example of problem solving
In a closed vessel with rigid walls containing an ideal gas, as a result of heating, the pressure increased by 3 times. It is necessary to determine the final temperature of the system if its initial value was 25 oC.
First, let's convert the temperature from degrees Celsius to Kelvin, we have:
T=25 + 273, 15=298, 15 K.
Since the walls of the vessel are rigid, the heating process can be considered isochoric. For this case, we apply the Gay-Lussac law, we have:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Thus, the final temperature is determined from the product of the pressure ratio and the initial temperature. Substituting the data into equality, we get the answer: T2=894.45 K. This temperature corresponds to 621.3 oC.






